Nachtermin Teil B

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

Die Parabel $p_1$ mit dem Scheitel $S(0{,}5|1)$ hat eine Gleichung der Form $y=0{,}5x^2+bx+c\quad(\mathbb{G}=\mathbb{R}\times\mathbb{R};~b\in\mathbb{R};~c\in\mathbb{R})$ .

Die Parabel $p_2$ hat die Gleichung $y=0{,}5x^2+3\quad(\mathbb{G}=\mathbb{R}\times\mathbb{R})$ . Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

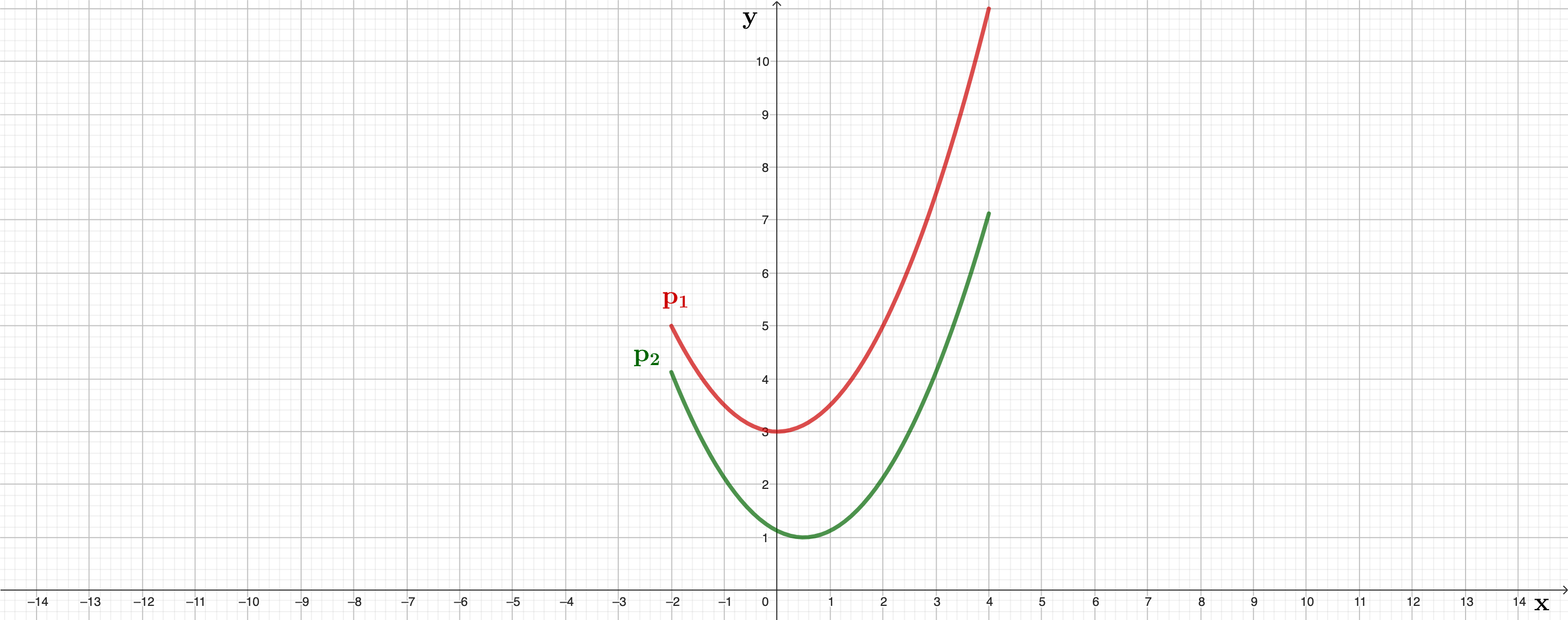
Zeigen Sie durch Berechnung der Werte für $b$ und $c$ , dass die Parabel $p_1$ die Gleichung $y=0{,}5x^2-0{,}5x+1{,}125$ hat. Zeichnen Sie sodann die Parabeln $p_1$ und $p_2$ für $x\in[-2;4]$ in ein Koordinatensystem ein.
Für die Zeichnung: Längeneinheit $1~\text{cm}$ ; $-2\le x\le 4;~0\le y\le 11$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform
Die allgemeine Scheitelform einer quadratischen Gleichung sieht folgendermaßen aus:
$\ \boxed{\mathrm{a(x-e)^2+d=0}}$
Bekannt ist: $\ \mathrm{a=0{,}5;\qquad e=0{,}5;\qquad d=1}$
Eingesetzt in die obige Formel gibt: $\ \mathrm{y=0{,}5\cdot(x-0{,}5)^2+1}\hspace{15mm}\mathbb{G=R}\ \text{x}\ \mathbb{R}$
Multipliziere aus: $\ \mathrm{y=0{,}5\cdot(x^2-x+0{,}25)+1}$
$\hspace{25mm}\Rightarrow\mathrm{ p_{1}:y=0{,}5x^2-0{,}5x+1{,}125}$
Einzeichnen der Parabeln $\ \mathrm{p_1}$ und $\ \mathrm{p_2}$ :
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Stelle die Scheitelform auf und multipliziere aus.

Berechnen Sie die Koordinaten des Schnittpunkts $T$ der Parabeln $p_1$ und $p_2$ .

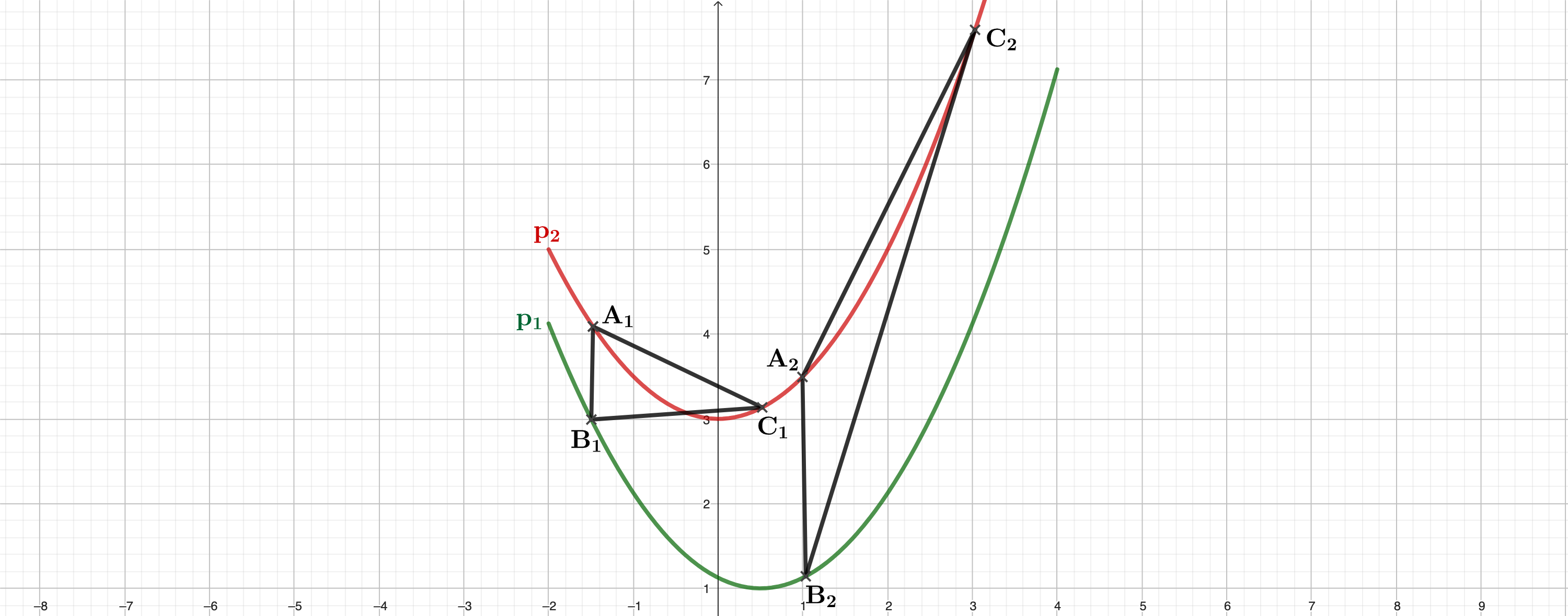
Punkte $A_n(x|0{,}5x^2+3)$ auf der Parabel $p_2$ haben dieselbe Abszisse $x$ wie Punkte $B_n(x|0{,}5x^2-0{,}5x+1{,}125)$ auf der Parabel $p_1$ . Sie sind für $x>-3{,}75$ zusammen mit Punkten $C_n$ die Eckpunkte von Dreiecken $A_nB_nC_n$ .
Die Punkte $C_n$ liegen auf der Parabel $p_2$ , wobei die Abszisse der Punkte $C_n$ stets um 2 größer ist als die Abszisse $x$ der Punkte $A_n$ .
Zeichnen Sie das Dreieck $A_1B_1C_1$ für $x=-1{,}5$ und das Dreieck $A_2B_2C_2$ für $x=1$ in das Koordinatensystem zu Teilaufgabe (a) ein.
Zeigen Sie sodann, dass sich die Koordinaten der Punkte $C_n$ in Abhängigkeit von der Abszisse $A_n$ wie folgt darstellen lassen: $C_n(x+2|0{,}5x^2+2x+5)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Das zweidimensionale kartesische Koordinatensystem
Einzeichnen der Dreiecke $\mathrm{A_1B_1C_1}$ und $\mathrm{A_2B_2C_2}$ in das Koordinatensystem
zu Teilaufgabe (a).
Darstellen der Koordinaten der Punkte $\mathrm{C_n}$ im Koordinatensystem in Abhängigkeit von der Abszisse $\mathrm{A_n}$ .
Setze für $\text{x}$ , $\mathrm{(x+2)}$ in die Funktionsgleichung zu $\mathrm{p_2}$ ein.
$\mathrm{C_n\Bigl(x+2\ |\ 0{,}5\cdot(x+2)^2+3\Bigr)\qquad x\in\mathbb{R};\ x>-3{,}75}$
$\mathrm{C_n\left(x+2\ |\ 0{,}5x^2+2x+5\right)}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestätigen Sie durch Rechnung, dass für die Länge der Strecke $[A_nB_n]$ in Abhängigkeit von der Abszisse $x$ der Punkte $A_n$ gilt:
$\overline{A_nB_n}(x)=(0{,}5x+1{,}875)~\text{LE}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionen und Gleichungen
$\mathrm{{p_2}:\ y=0{,}5x^2+3;\qquad {p_1}:y=0{,}5x^2-0{,}5x+1{,}125}$
$\mathrm{\overline{A_nB_n}(x)=\Bigl(0{,}5x^2+3-(0{,}5x^2-0{,}5x+1{,}125)\Bigr)LE}\qquad\qquad \text{x}\in\mathbb{R};\ \text{x}>-3{,}75$
$\mathrm{\overline{A_nB_n}(x)=0{,}5x+1{,}875\ LE}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Unter den Dreiecken $A_nB_nC_n$ gibt es das rechtwinklige Dreieck $A_3B_3C_3$ mit der Hypotenuse $[A_3C_3]$ .

Bestimmen Sie rechnerisch die Koordinaten des Punktes $B_3$ .

Unter den Dreiecken $A_nB_nC_n$ gibt es das gleichschenklige Dreieck $A_4B_4C_4$ mit der Basis $[A_4B_4]$ .

Bestimmen Sie rechnerisch den zugehörigen Wert für $x$ .

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
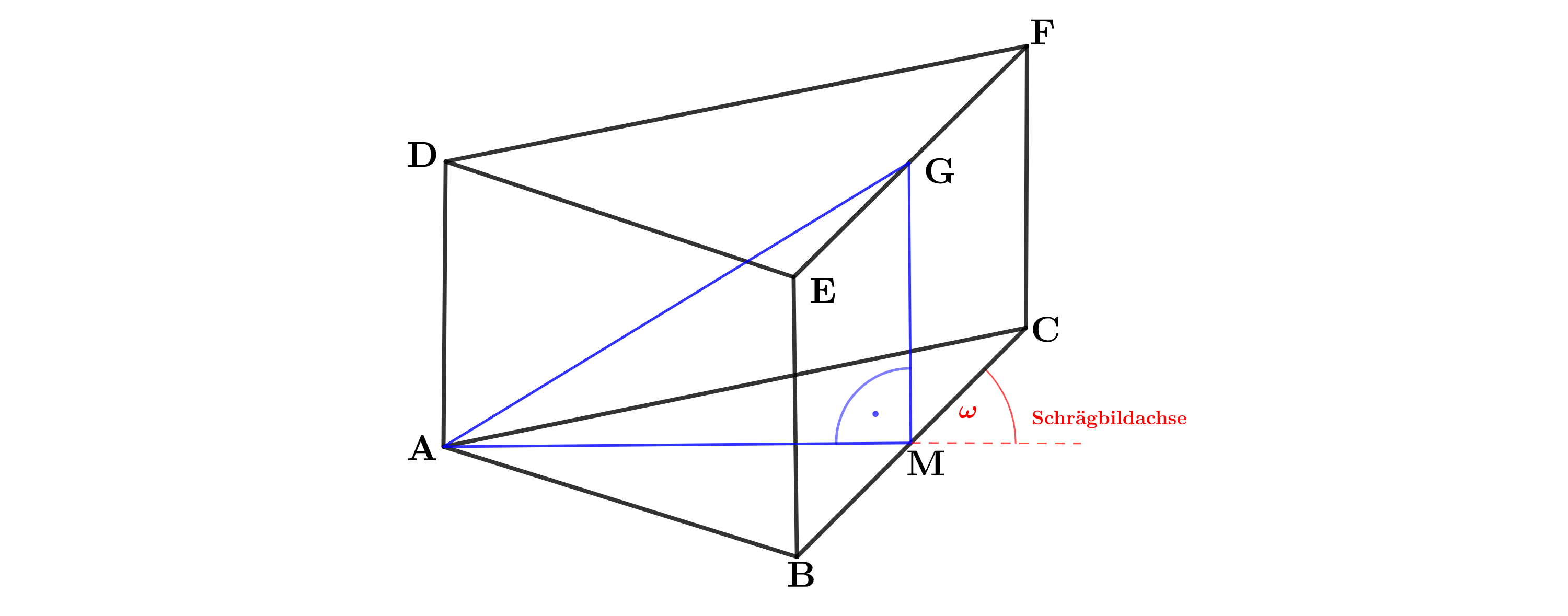
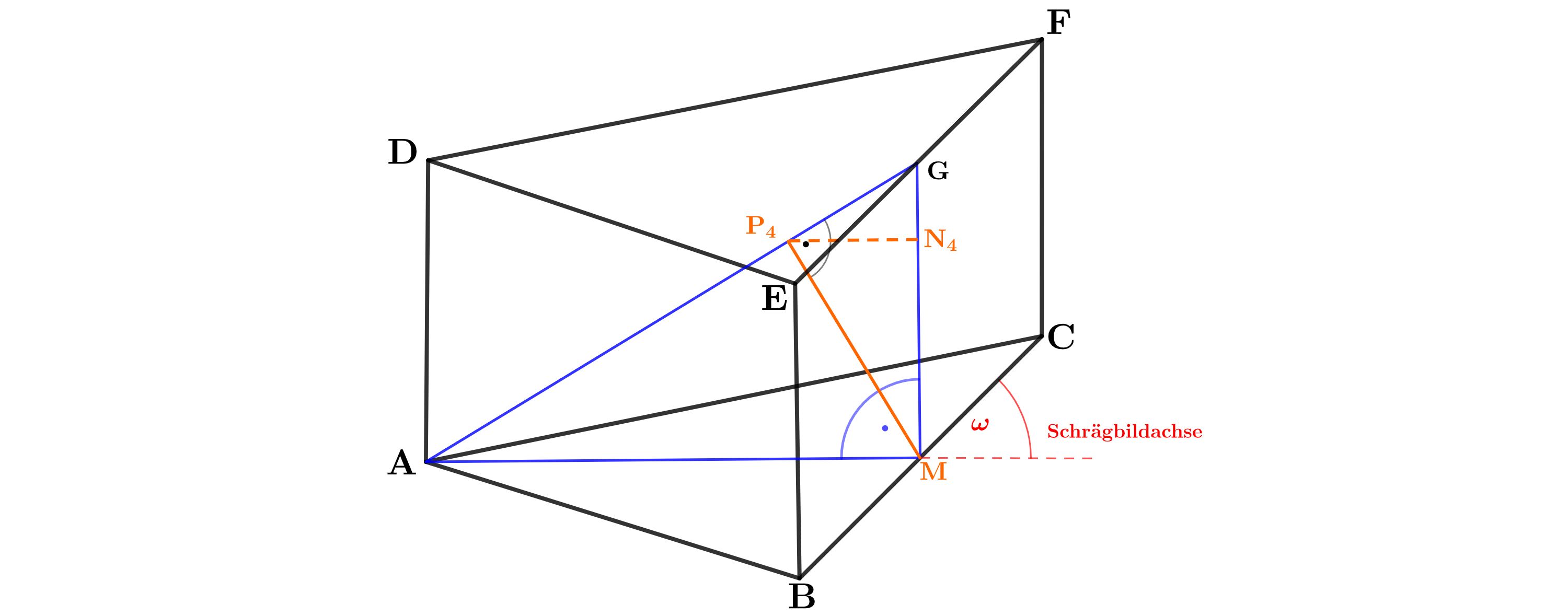
Die nebenstehende Skizze zeigt ein Schrägbild des Prismas $ABCDEF$ , dessen Grundfläche das gleichschenklige Dreieck $ABC$ mit der Basis $[BC]$ ist. Der Punkt $D$ liegt senkrecht über dem Punkt $A$ . Der Punkt $M$ ist der Mittelpunkt der Strecke $[BC]$ und der Punkt $G$ ist der Mittelpunkt der Strecke $[EF]$ .
Es gilt: $\overline{BC}=14~\text{cm};~\overline{AM}=10~\text{cm};~\overline{AD}=6~\text{cm}$
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
1. Zeichnen Sie das Schrägbild des Prismas $ABCDEF$ , wobei die Strecke $[AM]$ auf der Schrägbildachse und der Punkt $A$ links von $M$ liegen soll.
  Für die Zeichnung gilt: $q=0{,}5;~\omega=45^\circ$
  Zeichnen Sie sodann die Strecke $[AG]$ in das Schrägbild ein und berechnen Sie deren Länge sowie das Maß $\varphi$ des Winkels $AGM$ .
  $[$ Ergebnis: $\varphi=59{,}04^\circ]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras
  Satz des Pythagoras angewandt auf das Dreieck $\text{AMG}$ :
  $\ \mathrm{\overline{AG}^2=\overline{AM}^2+{\overline{GM}^2}}\Rightarrow\mathrm{\overline{AG}=\sqrt{\overline{AM}^2+\overline{GM}^2}}$
  Einsetzten der Zahlenwerte:
  $\ \mathrm{\overline{AG}=\sqrt{10^2+6^2}\ \ cm}\ \Rightarrow\ \boxed{\mathrm{\overline{AG}=11{,}66\ cm}}$
  Berechnen des Maßes $φ$ des Winkels $\text{AGM}$ :
  $\mathrm{tan\ \varphi=\dfrac{\overline{AM}}{\overline{GM}}}\ \Rightarrow\ \tan\ \varphi=\dfrac{10}{6}\ \Rightarrow\ \boxed{\varphi=59{,}04^{\circ}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Strecke $\ \mathrm{\overline{AG}}\$ mithilfe des Satz des Pythagoras.
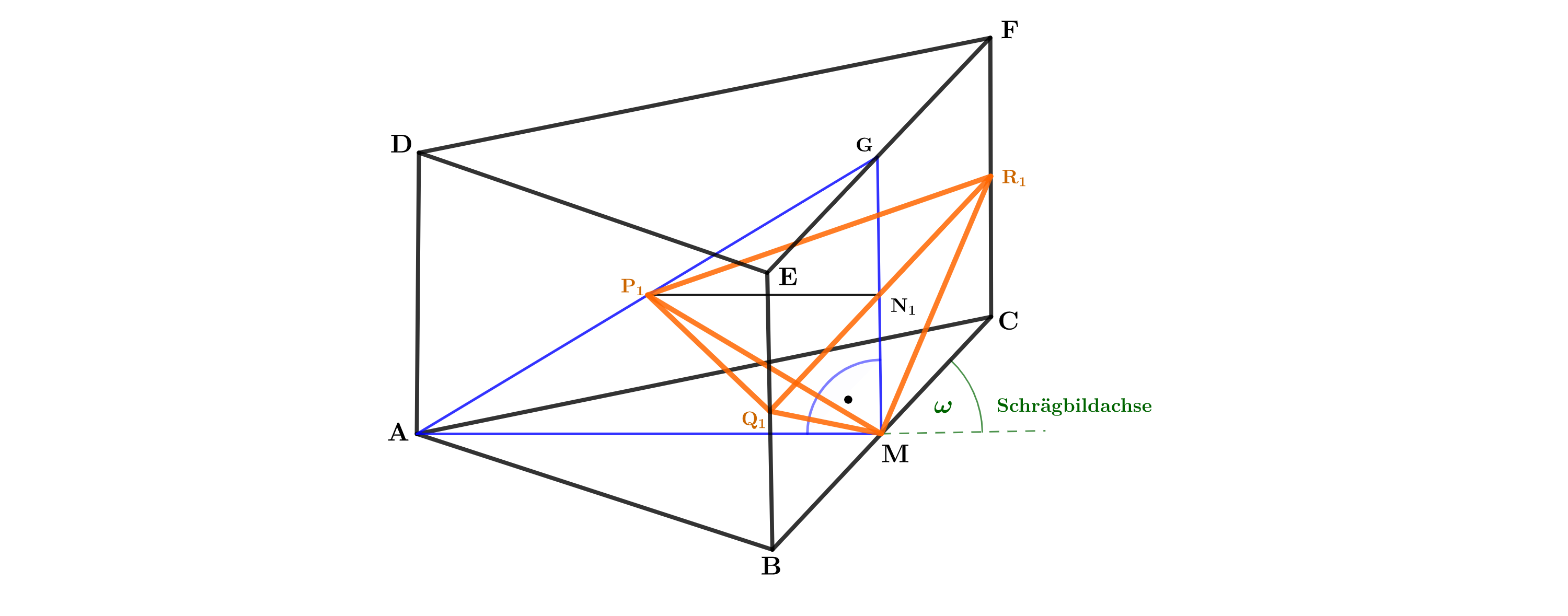
2. Ebenen, die zur Grundfläche $ABC$ parallel sind, schneiden $[AG]$ in Punkten $P_n$ , $[BE]$ in Punkten $Q_n$ , $[CF]$ in Punkten $R_n$ und $[MG]$ in Punkten $N_n$ .
  Es gilt: $\overline{GN_n}(x)=x~\text{cm}$ mit $x\in\mathbb{R}$ sowie $0<x<6$ .
  Der Punkt $M$ ist die Spitze von Pyramiden $P_nQ_nR_nM$ mit Dreiecken $P_nQ_nR_n$ als Grundfläche.
  Zeichnen Sie die Strecke $[GM]$ , den Punkt $N_1$ sowie die Pyramide $P_1Q_1R_1M$ für $x=3$ in das Schrägbild zur Teilaufgabe (a) ein.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder zeichnen
  Einzeichnen der Pyramide $\mathrm{P_1Q_1R_1M}$ in das Schrägbild zur Teilaufgabe $\text{(a)}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Zeigen Sie rechnerisch, dass sich das Volumen $V$ der Pyramiden $P_nQ_nR_nM$ in Abhängigkeit von $x$ wie folgt darstellen lässt: $V(x)=(-3{,}90x^2+23{,}38x)~\text{cm}^3$ .
  $[$ Teilergebnis: $\overline{P_nN_n}(x)=1{,}67x~\text{cm}]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Das Volumen der Pyramide $\mathrm{P_nQ_nR_nM}$ berechnet sich wie folgt:
  $\ V=\dfrac{1}{3}\cdot\dfrac{1}{2}\mathrm{\cdot\overline{P_nN_n}\cdot\overline{Q_nR_n}\cdot\overline{N_nM}}\hspace{40mm}\mathrm{\overline{Q_nR_n}=\overline{BC}}$
  Berechnen der Strecke $\mathrm{\overline{P_nN_n}}$ mit dem Tangens.
  $\ \mathrm{\dfrac{\overline{P_nN_n}(x)}{x\ cm}=tan\varphi\hspace{20mm}\varphi=59{,}04^\circ\hspace{20mm}x\in\mathbb{R};\ 0<x<6}$
  $\ \mathrm{\overline{P_nN_n} =1{,}67x\ cm}$
  $\ \mathrm{V(x)=\dfrac{1}{3}\cdot\dfrac{1}{2}\cdot1{,}67x\cdot14\cdot(6-x)\ cm^3\hspace{27mm}x\in\mathbb{R};\ 0<x<6}$
  $\ \mathrm{V(x)=\left(-3{,}90x^2+23{,}38x\right)\ cm^3}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne zuerst $\mathrm{\overline{P_nN_n}}$
4. Unter den Pyramiden ${P_nQ_nR_nM}$ hat die Pyramide $P_0Q_0R_0M$ das maximale Volumen.
  Berechnen Sie, um wie viel Prozent das Volumen der Pyramide $P_0Q_0R_0M$ kleiner ist als das Volumen des Prismas $ABCDEF$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Parabel
  Da es sich bei dem Funktionsgraphen von $\text{V(x)}$ um eine nach unten geöffnete Parabel handelt, entspricht der Funktionswert des Scheitels $\mathrm{y_S}$ , dem maximalen Volumen der Pyramide $\mathrm{P_nQ_nR_nM}$ .
  Berechnen des Funktionswertes $\mathrm{y_S}$ mit der Formel:
  $\ \mathrm{{y_S}=c-\dfrac{b^2}{4\cdot a}}$
  Zur Erinnerung, die allgemeine Form einer quadratischen Funktion lautet:
  $\ \mathrm{f\left( x\right)={ax}^2+{bx}+ c}$
  $\ \mathrm{y_S}=0-\dfrac{(23{,}38)^2}{4\cdot (-3{,}90)}\ \Rightarrow\ y_S=-\dfrac{546{,}62}{-15{,}60}$
  $\ \mathrm{{y_S}=35{,}04}$
  Das maximale Volumen der Pyramide $\mathrm{P_0Q_0R_0M}$ beträgt: $\boxed{\mathrm{V_{P_0Q_0R_0M}=35{,}04\ cm^3}}$
  Volumen Prisma: $\ \mathrm{V_{ABCDEF}=\dfrac{\overline{BC}\cdot \overline{AM}{2}\cdot\overline{AD}}\ \Rightarrow\ V_{ABCDEF}=\dfrac{14\cdot10}{2}\cdot6\ [cm^3}]$
  $\hspace{26mm}\mathrm{V_{ABCDEF}=420\ cm^3}$
  Berechnen des prozentualen Unterschieds von $\mathrm{V_{ABCDEF}}$ zu $\mathrm{V_{P_0Q_0R_0M}}$ :
  $\dfrac{420-35{,}04}{420}=0{,}9166$
  Das Volumen der Pyramide ist um $\boxed{91{,}66\ \%}$ kleiner als das Volumen des Prismas.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Ermittle den Funktionswert $\mathrm{y_S}$ von $\mathrm{V(x)=(-3{,}90x^2+23{,}38x)}$
5. Die Pyramiden $P_2Q_2R_2M$ und $P_3Q_3R_3M$ haben jeweils ein Volumen von $7{,}5~\text{cm}^3$ .
  Berechnen Sie die zugehörigen Werte für $x$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichung
  $\ \mathrm{V_{P_2Q_2R_2M}=V_{P_3Q_3R_3M}=7{,}5\ cm^3}$
  $\mathrm{-3{,}90x^2+23{,}38x=7{,}5\hspace{35mm}x\in\mathbb{R};\ 0<x<6}$
  Löse die quadratische Gleichung z.B. mit der Mitternachtsformel.
  $\ x_{1/2}=\dfrac{-23{,}38\pm\sqrt{23{,}38^2-4\cdot(-3{,}90\cdot-7{,}5)}}{2\cdot(-3{,}90)}$
  $\ x_{1/2}=\dfrac{-23{,}38\pm\sqrt{546{,}62-117}}{-7{,}80}$
  $\ \mathrm{x=0{,}34\qquad\lor\qquad x=5{,}65\hspace{25mm}\mathbb{L}=\{0{,}34;\ 5{,}64\}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze $\mathrm{V(x)=7{,}5}$ und löse die quadratische Gleichung.
6. Zeigen Sie, dass für die Längen der Strecken $[P_nM]$ in Abhängigkeit von $x$ gilt:
  $\overline{P_nM}(x)=\sqrt{3{,}79x^2-12x+36}~\text{cm}$ .
  Unter den Strecken $[P_nM]$ hat die Strecke $[P_4M]$ die minimale Länge.
  Zeichnen Sie die Strecken $[P_4M]$ in das Schrägbild zur Teilaufgabe (a) ein und berechnen Sie deren Länge.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras
  Einzeichnen der Strecke $\mathrm{[P_4M].}$
  $\ \mathrm{[P_nM]}$ in Abhängigkeit von $\text{x}:$
  $1.$ Lösungsmöglichkeit:
  $\ \mathrm{\overline{P_nM}(x)=\sqrt{(\overline{P_nN_n})^2+(\overline{N_nM})^2}\qquad\qquad \overline{P_nN_n}=1{,}67x\qquad \overline{N_nM}=(6-x)}$
  $\ \mathrm{\overline{P_nM}(x)=\sqrt{(1{,}67x)^2+(6-x)^2}\ cm}\hspace{20mm}\text{x}\in\mathbb{R};\ \mathrm{0<x<6}$
  $\ \mathrm{\overline{P_nM}(x)=\sqrt{3{,}79x^2-12x+36}~\text{cm}}$
  Berechnen der Strecke $\mathrm{\overline{P_4M}}:$
  Da es sich bei dem Funktionsgraphen von $\mathrm{(\overline{P_nM})^2}$ um eine nach oben geöffnete Parabel handelt, entspricht der Funktionswert des Scheitels $\mathrm{y_S}$ dem Quadrat der minimalen
  Länge der Strecke $\mathrm{\overline{P_4M}}.$
  Berechnen des Funktionswertes $\mathrm{y_S}$ mit der Formel:
  $\mathrm{y_S=c-\dfrac{b^2}{4\cdot a}\ \Rightarrow\ y_S=36-\dfrac{12^2}{4\cdot 3{,}79}\ cm^2}$
  $\ \mathrm{y_S=26{,}50\ cm^2}$
  $\mathrm{(\overline{P_4M})^2=26{,}50\ cm^2\ \Rightarrow\ \overline{P_4M}=\sqrt{26{,}50\ cm^2}}$
  $\ \mathrm{\overline{P_4M}=5{,}15\ cm}$
  $\rule{12cm}{0.5mm}$
  $2.$ Lösungsmöglichkeit:
  Das Dreieck $\mathrm{\vartriangle{AMP_4}}$ ist ein rechtwinkliges Dreieck, der Winkel $\mathrm{\sphericalangle{AMP_4}}$ ist bekannt,
  siehe Lösung zur Aufgabe $\mathrm{2a).}$ $\mathrm{\overline{P_4M}}$ ist dann die Ankathete und $\mathrm{\overline{AM}}$ ist die Hypotenuse
  dieses Dreiecks.
  $\mathrm{\cos\sphericalangle{AMP_4}=\dfrac{\overline{P_4M}}{\overline{AM}}\ \Rightarrow\ \overline{P_4M}=\cos\sphericalangle{AMP_4}\cdot\overline{AM}}$
  $\ \mathrm{\overline{P_4M}=10\ cm\cdot cos\ 59{,}04^{\circ}\ \Rightarrow\ \overline{P_4M}=10\ cm\cdot 0{,}5144}$
  $\ \mathrm{\overline{P_4M}=5{,}14\ cm}$
  Der Unterschied der Ergebnisse kommt daher, dass der in der $1.$ Lösungsmöglichkeit
  verwendet Wert $(1{,}67)$ aufgerundet ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \mathrm{0{,}5x^2-0{,}5x+1{,}125}$	$=$	$\displaystyle \mathrm{0{,}5x^2+3}$	$\displaystyle -0{,}5x^2$
	↓	subtrahiere
$\displaystyle -0{,}5x+1{,}125$	$=$	$\displaystyle 3$	$\displaystyle -1{,}125$
	↓	subtrahiere
$\displaystyle -0{,}5x$	$=$	$\displaystyle 1{,}875$	$\displaystyle \cdot(-2)$
	↓	multipliziere
$\displaystyle \text{x}$	$=$	$\displaystyle -3{,}75$

$\displaystyle \mathrm{0{,}5x^2-0{,}5x+1{,}125}$	$=$	$\displaystyle \mathrm{0{,}5x^2+2x+5}$	$\displaystyle \mathrm{-0{,}5x^2\qquad\qquad \text{x}\in\mathbb{R};\ x>-3{,}75}$
	↓	subtrahiere
$\displaystyle \mathrm{-0{,}5x+1{,}125}$	$=$	$\displaystyle \mathrm{2x+5}$	$\displaystyle \mathrm{-2x}$
	↓	subtrahiere
$\displaystyle \mathrm{-2{,}5x+1{,}125}$	$=$	$\displaystyle 5$	$\displaystyle -1{,}125$
	↓	subtrahiere
$\displaystyle \mathrm{-2{,}5x}$	$=$	$\displaystyle 3{,}875$	$\displaystyle :-2{,}5$
	↓	dividiere
$\displaystyle \text{x}$	$=$	$\displaystyle -1{,}55$

$\displaystyle 0{,}5x^2-0{,}25x+2{,}06$	$=$	$\displaystyle \mathrm{0{,}5x^2+2x+5}$	$\displaystyle \mathrm{-0{,}5x^2\qquad\qquad \mathbb{G}\in\mathbb{R};\ x>-3{,}75}$
	↓	subtrahiere
$\displaystyle \mathrm{-0{,}25x+2{,}06}$	$=$	$\displaystyle \mathrm{2x+5}$	$\displaystyle \mathrm{-2x-2{,}06}$
	↓	subtrahiere
$\displaystyle \mathrm{-2{,}25x}$	$=$	$\displaystyle 2{,}94$	$\displaystyle \mathrm{:-2{,}25}$
	↓	dividiere
$\displaystyle \text{x}$	$=$	$\displaystyle -1{,}31$	$\displaystyle \hspace{28mm}\mathbb{L}=\{-1{,}31\}$

Nachtermin Teil B

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?