Aufgabe 2A
Die Sektoren des abgebildeten Glücksrads sind gleich groß und mit den Zahlen von 0 bis 9 beschriftet.
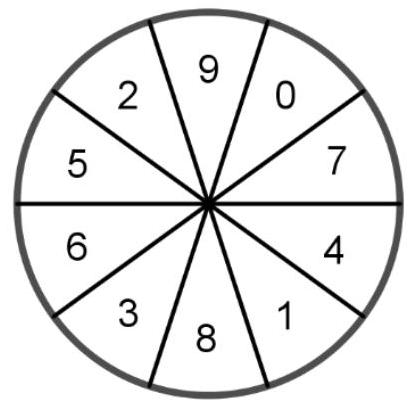
Das Glücksrad wird zwanzigmal gedreht.
Bestimmen Sie die Wahrscheinlichkeiten der Ereignisse und . (5 BE)
: „Es wird genau siebenmal eine ungerade Zahl erzielt.“
: „Es wird mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt.“
Das Glücksrad wird zweimal gedreht.
Untersuchen Sie, ob die Ereignisse und stochastisch unabhängig sind. (5 BE)
: „Die Summe der erzielten Zahlen ist kleiner als
: „Das Produkt der erzielten Zahlen ist 2 oder 3.“
Mit dem Glücksrad wird ein Spiel durchgeführt. Jeder Spieler darf das Glücksrad beliebig oft drehen. Beendet er das Spiel selbst, bevor er eine „0“ erzielt, so wird ihm die Summe der erzielten Zahlen in Euro ausgezahlt. Erzielt er eine „ 0 “, so ist das Spiel dadurch beendet und es erfolgt keine Auszahlung.
Bei einem Spieler beträgt nach mehrmaligem Drehen des Glücksrads die Summe der erzielten Zahlen 60. Er dreht das Glücksrad genau ein weiteres Mal.
Berechnen Sie den Erwartungswert für den ausgezahlten Betrag. (3 BE)
Der Spieler dreht das Glücksrad bis er eine „ 0 “ erzielt, aber höchstens -mal. Der Erwartungswert für die Auszahlung beträgt in diesem Fall .
Beurteilen Sie die folgende Aussage: (4 BE)
Es gibt zwei, aber nicht drei aufeinanderfolgende Werte von n, für die die Erwartungswerte für die Auszahlung übereinstimmen.
Betrachtet wird nun ein Glücksrad mit 10 nicht gleich großen Sektoren. Die Sektoren sind mit den Zahlen von 0 bis 9 beschriftet.
Bei 80 Drehungen wird zwölfmal die „0“ erzielt. Auf dieser Grundlage wird zur Sicherheitswahrscheinlichkeit ein Konfidenzintervall für die Wahrscheinlichkeit, bei einer Drehung die "0“ zu erzielen, bestimmt.
Begründen Sie, dass die obere Grenze des Konfidenzintervalls größer als 0,1 ist. (4 BE)
Bestimmen Sie die kleinste Anzahl an Drehungen, für die Folgendes gilt: (4 BE)
Wenn man bei genau der Drehungen die „0" erzielt, dann steht dies bei einer Sicherheitswahrscheinlichkeit von nicht in Einklang mit der Annahme, dass beim Drehen des Glücksrads die „0" mit einer Wahrscheinlichkeit von erzielt wird.
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
