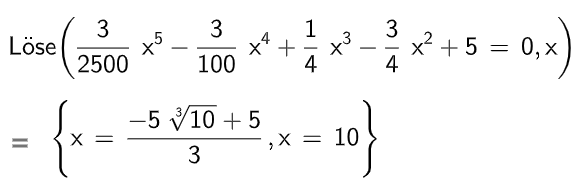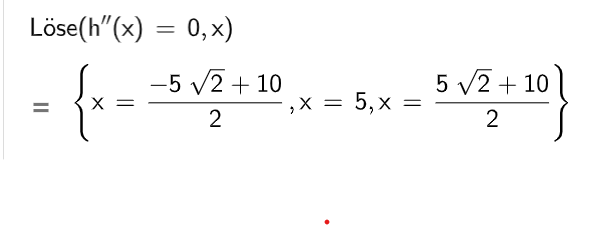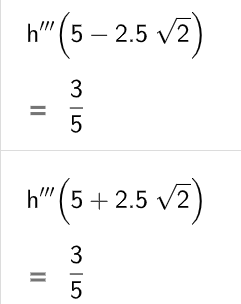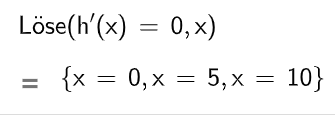Aufgabe 1B
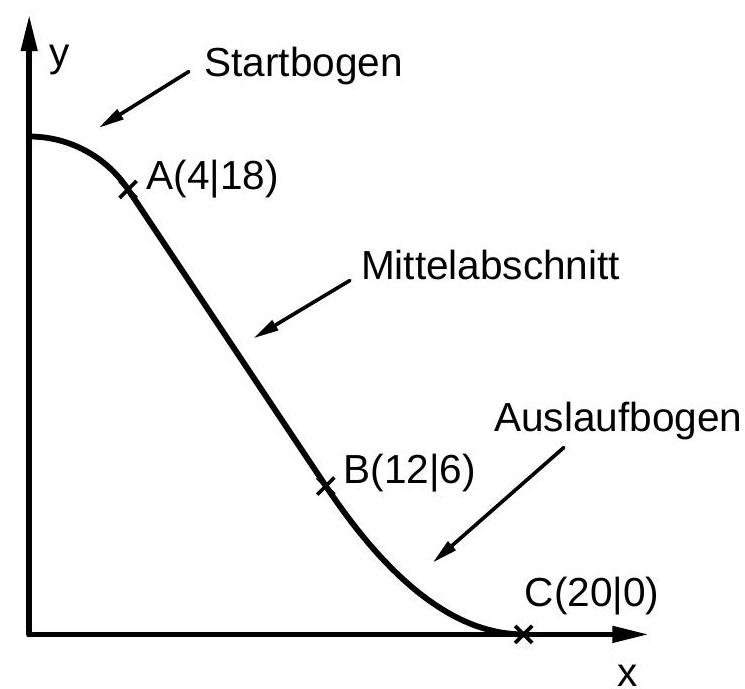
Die nebenstehende Abbildung zeigt schematisch die Seitenansicht einer Wasserrutschbahn, die aus einem Startbogen, einem Mittelabschnitt und einem
Auslaufbogen zusammengesetzt ist. Die einzelnen Abschnitte werden durch Funktionen beschrieben.
Die Funktionen stimmen in den jeweiligen Übergängen in Funktionswerten und Werten der Ableitung überein. Der Auslaufbogen hat in seinem Endpunkt eine waagerechte Tangente. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit. Die -Achse beschreibt die Horizontale.
Berechnen Sie eine Gleichung der Gerade, die den Mittelabschnitt beschreibt.
Berechnen Sie die Größe des Winkels dieses Abschnitts der Rutschbahn gegenüber der
Horizontalen. [Zur Kontrolle: ] (6 BE)
Der Auslaufbogen wird mithilfe einer quadratischen Funktion beschrieben.
Bestimmen Sie eine Gleichung von . (4 BE)
[Zur Kontrolle: ]
Die Seitenfläche unterhalb der Wasserrutschbahn wird im Bereich verkleidet.
Stellen Sie die entsprechende Fläche in der Abbildung grafisch dar.
Berechnen Sie den Flächeninhalt der Seitenfläche. (6 BE)
Der Startbogen wird mithilfe eines Kreises beschrieben. Er wird durch mehrere Streben gleicher Länge gestützt; diese gehen alle vom selben Punkt aus, der auf der -Achse liegt. Eine der Streben stößt direkt am Übergang zwischen Startbogen und Mittelabschnitt senkrecht auf die Rutschbahn.
Weisen Sie nach, dass der Mittelpunkt des Kreises die Koordinaten hat.
(3 BE)
Berechnen Sie den Radius des Kreises. (3 BE)
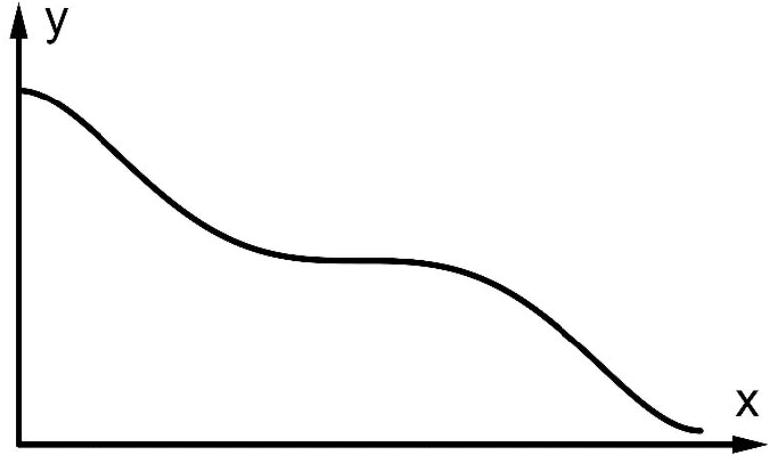
Die nebenstehende Abbildung zeigt die vollständige schematische Seitenansicht einer zweiten Wasserrutschbahn. Ihr Verlauf wird mithilfe der in definierten Funktion mit beschrieben. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit. Die -Achse beschreibt die Wasseroberfläche. Die Rutschbahn endet Meter oberhalb der Wasseroberfläche.
Geben Sie die Höhe des Startpunkts der Rutschbahn oberhalb der Wasseroberfläche an.
Ermitteln Sie die Koordinaten des Endpunktes der Rutschbahn. (4 BE)
Die Rutschbahn weist in mehreren Punkten ihre größte Neigung gegenüber der Horizontalen auf.
Berechnen Sie diese Neigung in Prozent. (4 BE)
Der Graph von enthält Punkte, in denen die Tangente an den Graphen parallel zur -Achse verläuft.
Weisen Sie nach, dass diese Punkte alle auf einer Geraden liegen. (5 BE)
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen