Gegeben sind drei Dreiecke mit folgenden Maßen:
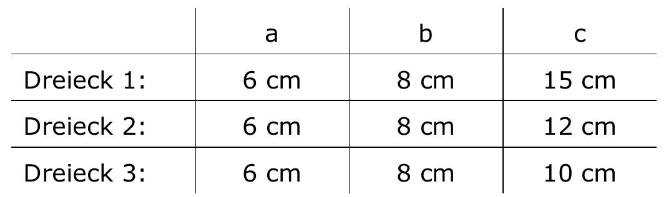
Begründe:
Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt.
serlo.orgDieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt.
→ Was bedeutet das?