Heft 2 - B2
🎓 Prüfungsbereich für Schleswig-Holstein
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Aufgaben und Lösungen des Mathe MSA 2022 Prüfungsteil 2 Aufgabe 2.
Ein Taschenrechner ist in diesem Prüfungsteil erlaubt.
- 1
In vielen Städten gibt es Litfaßsäulen. Das sind große Zylinder aus Beton, auf denen Plakate kleben. Lutz arbeitet bei einer Firma, die Litfaßsäulen beklebt.

Die Abbildung ist nicht maßstabsgetreu.
Lutz überlegt, wie die abgebildete Säule beklebt werden soll. Dazu hat er eine Skizze der beklebbaren Fläche angefertigt (siehe Abbildung). Die Seitenlängen und berechnet ein Computerprogramm.
Kreuze an, wie berechnet wurde. (1 Punkt)
Kreuze an, wie berechnet wurde. (1 Punkt)
Ein Plakat im DIN-A0-Format ist lang und breit.
Ermittle, wie viele DIN-A0-Plakate ohne Überlappung auf die Säule geklebt werden können, wenn alle Plakate dieselbe Ausrichtung haben. (2 Punkte)
- 2
Das zylindrische Dach der Litfaßsäule muss erneuert werden.
Berechne das Volumen des alten Daches in . (2 Punkte)
Das neue Dach soll bei gleicher Grundfläche die Form eines Kegels haben und hoch sein.
Begründe, dass das neue Dach ein kleineres Volumen hat als das alte. (2 Punkte)
Damit keine Tauben auf dem neuen Dach landen, soll der Neigungswinkel betragen.
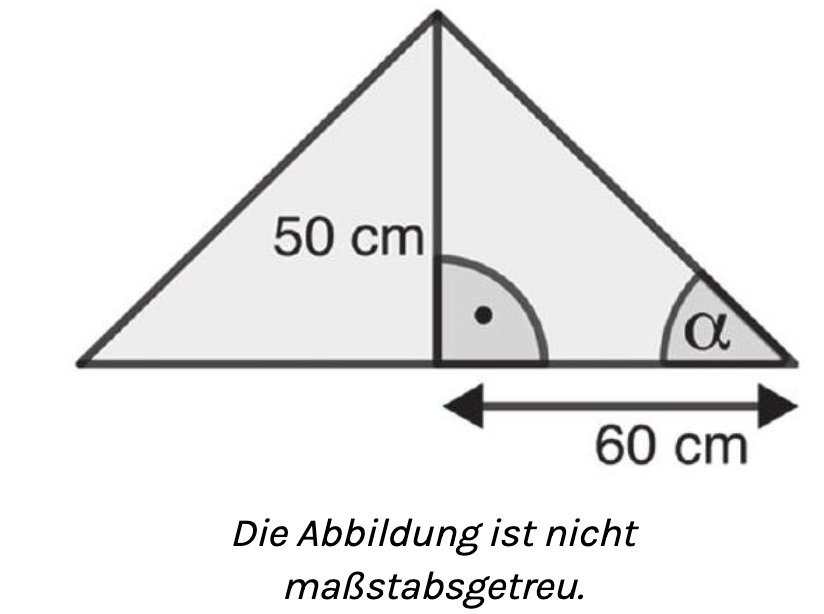
Begründe, dass der Neigungswinkel die Bedingung nicht erfüllt. (1 Punkt)
- 3
Die hohe Litfaßsäule wirft einen Schatten auf den Boden. Der Schatten ist lang. Lutz ist groß. Er möchte mit einem Experiment die Länge seines Schattens herausfinden. Dazu stellt er sich so in den Schatten der Litfaßsäule, dass sein eigener Schatten gerade im Schatten der Litfaßsäule verschwindet.
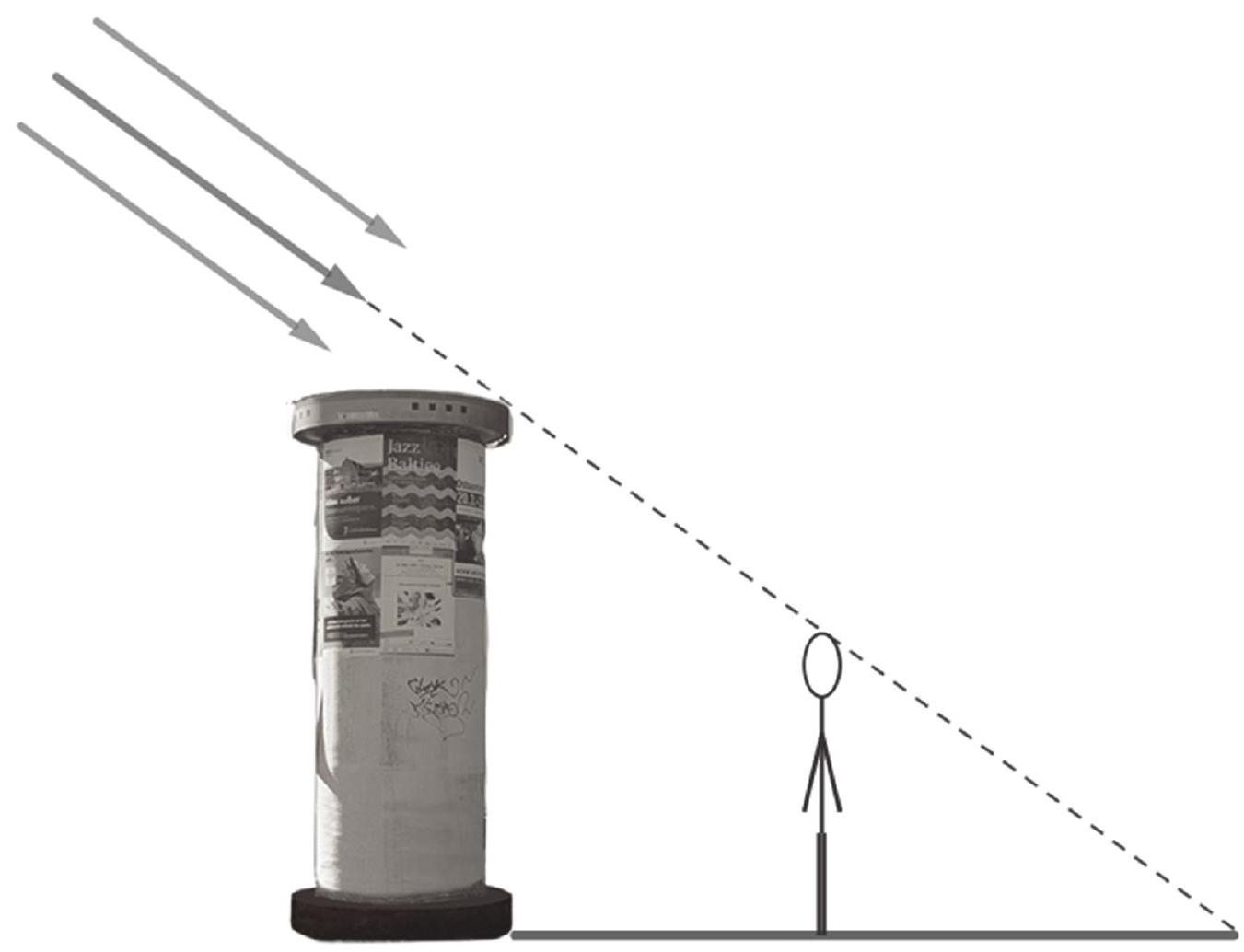
Die Abbildung ist nicht maßstabsgetreu.
Ergänze in der Abbildung die Größen aus dem Text. (1 Punkt)
Bestimme rechnerisch die Länge von Lutz' Schatten. (2 Punkte)
- 4
Lutz hat ein Modell der Litfaßsäule im Maßstab 1:6 gebastelt.
Gib die Höhe des Modells an. (1 Punkt)
Lutz möchte wissen, wie groß die beklebbare Fläche seines Modells ist. Dazu berechnet er den entsprechenden Flächeninhalt für die große Litfaßsäule und dividiert diesen Wert durch 6, also
Entscheide, ob Lutz richtig gerechnet hat und begründe deine Entscheidung. (2 Punkte)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?