Betrachtet wird die Schar der in definierten Funktionen
mit und . Die Funktion aus Aufgabe 1 ist eine Funktion dieser Schar.
Jeder der abgebildeten Graphen I, II und III der Schar gehört, bei festen
Werten von und , zu einem der Werte , und .
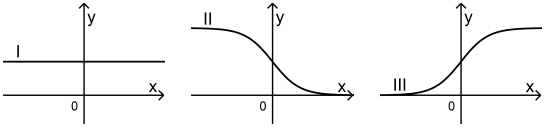
Ordnen Sie den Graphen die genannten Werte von zu und begründen
Sie Ihre Zuordnung.
Auf einer Inselgruppe wurden Seeadler neu angesiedelt. Betrachtet wird die anschließende Entwicklung der Anzahl der Seeadler. In einem Modell wird diese Entwicklung mithilfe des Graphen der Funktion beschrieben, die im Folgenden mit bezeichnet wird. Es gilt also . Dabei ist die seit der Ansiedlung vergangene Zeit in Jahren und die Anzahl der Seeadler.
Geben Sie auf Grundlage des Modells an, wie viele Seeadler angesiedelt wurden, und berechnen Sie, nach wie vielen Jahren die Anzahl der Seeadler auf angewachsen ist.
Die Tangente an den Graphen von im Punkt hat die Steigung . Würde die Entwicklung der Anzahl der Seeadler im Modell mithilfe dieser Tangente beschrieben werden, so ergäbe sich für den Zeitpunkt vier Jahre nach der Ansiedlung eine bestimmte Anzahl von Seeadlern. Untersuchen Sie, ob diese Anzahl mit derjenigen übereinstimmt, die sich bei einer Beschreibung mithilfe des Graphen von ergeben würde.
Unter bestimmten anderen Gegebenheiten auf der Inselgruppe kann die
Entwicklung der Anzahl der Seeadler im Modell mithilfe des Graphen einer
anderen Funktion aus der Schar der Funktionen beschrieben
werden. Das folgende Gleichungssystem ermöglicht die Bestimmung der
zugehörigen Werte von und .
(1) (2) (3)
Interpretieren Sie jede der drei Gleichungen im Sachzusammenhang.
Ermitteln Sie die Werte von und .
