Teil 2, Analysis I - lernen mit Serlo!

Gegeben sind die Funktionen $f: x\mapsto\dfrac{e^{2x}+e^x}{e^{2x}+1}$ und $F:x\mapsto \int f(t) \mathrm{d}t$ jeweils in ihren Definitionsmengen $D_f=\mathbb{R}$ und $D_F=\mathbb{R}$ . Es sei bekannt, dass der Graph von $F$ genau einen Wendepunkt besitzt.

Bestimmen Sie das Monotonieverhalten des Graphen von $F$ .
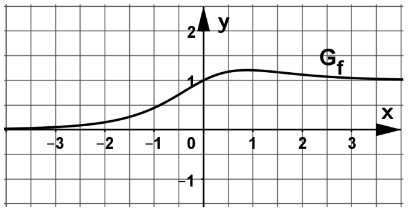
Im Schaubild, siehe unten, ist ein Teil des Graphen von $f$ abgebildet. Geben Sie nur unter Zuhilfenahme des Schaubilds die $x$ -und die $y$ -Koordinate des Wendepunkts des Graphen von $F$ näherungsweise an und begründen Sie jeweils Ihre Antwort.
Bestimmen Sie eine integralfreie Darstellung von $F (x)$ .
Hinweis: Die Substitution $z = e^{t}$ kann hilfreich sein.