S I

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

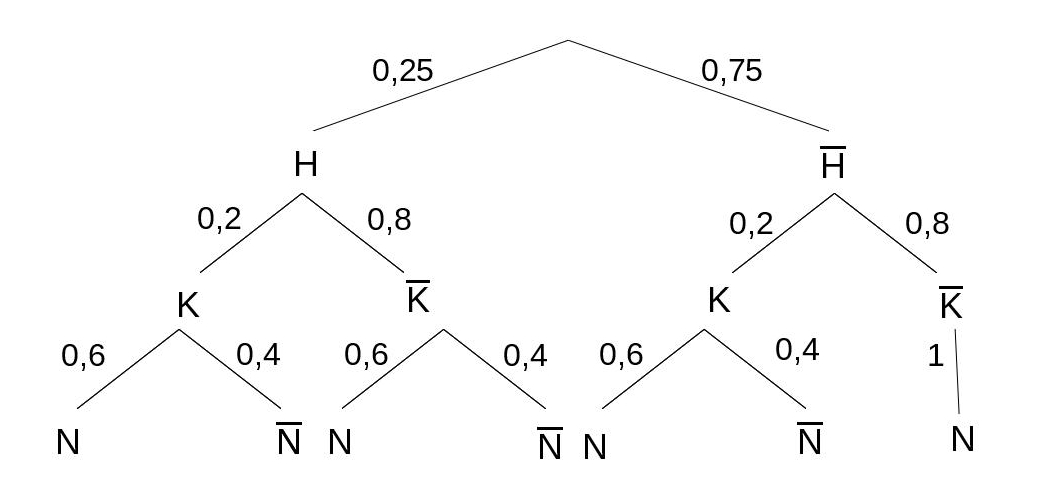
Die Glocken-Apotheke bietet ihren erkälteten Kunden Hustensaft (H), Kopfschmerztabletten (K) und Nasenspray (N) an, wobei jeder entsprechende Kunde mindestens eines dieser Produkte erwirbt. Im Folgenden werden nur diese drei Medikamente betrachtet.

Aus Erfahrung weiß der Apotheker, dass unabhängig voneinander 25% der Kunden einen Hustensaft erwerben und jeder fünfte Kunde Kopfschmerztabletten kauft. Kunden kaufen zu 60% auch ein Nasenspray, wenn sie mindestens eines der anderen Medikamente erwerben. Der Einkauf eines beliebig herausgegriffenen Kunden wird als Zufallsexperiment aufgefasst.

Erstellen Sie ein vollständiges Baumdiagramm und bestimmen Sie die Wahrscheinlichkeiten aller 7 Elementarereignisse. (5 BE)
[Teilergebnis: $P({H\overline{K}N})=0{,}12$ ]

Für diese Aufgabe benötigst Du folgendes Grundwissen: Pfadregen
Mögliche Lösung für das Baumdiagramm:
Berechnung der Teilwahrscheinlichkeiten
Diese kannst du mithilfe der Pfadregeln berechnen:
$\def\arraystretch{1.25} \begin{array}{lll} P(HKN)&=0{,}25\cdot 0{,}2\cdot 0{,}6&=0{,}03\\P(HK\overline{N})&=0{,}25\cdot 0{,}2\cdot 0{,}4&=0{,}02\\P(H\overline{K}N)&=0{,}25\cdot 0{,}8\cdot 0{,}6&=0{,}12\\P(H\overline{K}\overline{N})&=0{,}25\cdot 0{,}8\cdot 0{,}4&=0{,}08\\P(\overline{H}KN)&=0{,}75\cdot 0{,}2\cdot 0{,}6&=0{,}09\\P(\overline{H}K\overline{N})&=0{,}75\cdot 0{,}2\cdot 0{,}4&=0{,}06\\P(\overline{H}\overline{K}N)&=0{,}75\cdot 0{,}8\cdot 1&=0{,}6\end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Hinweise über die Reihenfolge des Baumdiagramms bekommst du sowohl im Text als auch aus dem Teilergebnis: Zuerst Hustensaft, dann Kopfschmerztabletten, dann Nasenspray.
Danach musst du den Ästen die richtigen Wahrscheinlichkeiten aus dem Text zuordnen.
Vergiss nicht am Ende die Wahrscheinlichkeiten aller Elementarereignisse mit den Pfadregeln zu berechnen.

Gegeben seien folgende Ereignisse:

$E_{1}$ : „Ein zufällig ausgewählter Kunde kauft keine Kopfschmerztabletten.“

$E_{2}$ : „Es wird Nasenspray und mindestens ein weiteres Produkt gekauft.“

$E_3=\overline{\overline{E_1} \cup E_2}$

Geben Sie diese Ereignisse in aufzählender Mengenschreibweise an. Beschreiben Sie $E_{3}$ möglichst einfach in Worten und berechnen Sie $P (E_{3})$ . (5 BE)

$E_{1}$ : „Ein zufällig ausgewählter Kunde kauft keine Kopfschmerztabletten.“

Du bist also auf der Suche nach allen Ergebnissen, wo ein $\overline{K}$ vorkommt. Das ist bei folgenden Ergebnissen der Fall:

$E_1=\{H\overline{K}N; H\overline{K}\overline{N}; \overline{H}\overline{K}N\}$

$E_{2}$ : „Es wird Nasenspray und mindestens ein weiteres Produkt gekauft.“

Du bist also auf der Suche nach allen Ergebnissen, wo ein $N$ und $H$ , $K$ oder beides vorkommt. Das ist bei folgenden Ergebnissen der Fall:

$E_2=\{HKN; H\overline{K}N; \overline{H}KN\}$

$E_3=\overline{\overline{E_1} \cup E_2}$

Um es dir einfacher zu machen, kannst du hier die Regel von De Morgan anwenden, um $E_{3}$ umzuformen:

$E_3=\overline{\overline{E_1} \cup E_2}=E_1\cap \overline{E_2}$

Deswegen sucht du alle Ergebnisse, die gleichzeitig in Ereignis $E_{1}$ , aber nicht in Ereignis $E_{2}$ sind (es muss beides gleichzeitig stimmen, weil du die Schnittmenge suchst).

Das ist bei folgenden Ergebnissen der Fall:

$E_3=\{H\overline{K}\overline{N}; \overline{H}\overline{K}N\}$

Möglichst einfache Formulierung

Für eine möglichst einfache Formulierung schaust du dir am besten die beiden Ergebnisse genauer an. Vielleicht fällt dir dabei auf, dass in beiden Fällen zweimal ein "Nicht" vorkommt. Bei beiden Ergebnissen wird also genau ein Medikament eingekauft, beim ersten nur Hustensaft und beim zweiten nur Nasenspray. Eine mögliche Formulierung könnte deshalb lauten:

Es wird entweder nur Hustensaft oder nur Nasenspray gekauft.

Wahrscheinlichkeit von $E_{3}$

Die Wahrscheinlichkeit von $E_{3}$ kannst du nach den Pfadregeln berechnen. Unterschiedliche Pfade müssen dabei addiert werden:

$\displaystyle P\left(E_3\right)$	$=$	$\displaystyle P\left(\left\{H\overline{K}\overline{N}\right\}\right)+P\left(\left\{\overline{H}\overline{K}N\right\}\right)$
	↓	Nun kannst du die Wahrscheinlichkeiten aus Teilaufgabe 1.1 einsetzen.
	$=$	$\displaystyle 0{,}08+0{,}6$
	$=$	$\displaystyle 0{,}68$

Die Wahrscheinlichkeit für $E_{3}$ beträgt $68 %$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Der Apotheker bietet seinen Kunden nur Hustensaft der Marken A und B an. Von 500 Hustensaftkäufern entscheiden sich 400 für den Hustensaft A. Bei 280 der Kunden, die Hustensaft A kaufen, tritt eine Verbesserung der Symptome ein. Von den Käufern der Hustensaftmarke B geben 30 an, dass keine Verbesserung der Symptome auftritt.

Stellen Sie für den beschriebenen Sachverhalt eine vollständige Vierfeldertafel auf, überprüfen Sie, ob die Ereignisse
A: „Ein Kunde kauft Hustensaft der Marke A.“ und
V: „Es tritt eine Verbesserung der Symptome auf.“
stochastisch unabhängig sind und interpretieren Sie Ihr Ergebnis im Sinne der vorliegenden Thematik. (5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
Vierfeldertafel
Du zeichnest zuerst eine leere Vierfeldertafel mit den beiden Ereignissen, die in der Aufgabenstellung angegeben sind. Anschließend kannst du die schwarzen Werte aus dem Text entnehmen und schließlich die roten Werte über Additionen und Subtraktionen ausrechnen, wie das genau funktioniert, wird im Artikel zu Vierfeldertafeln erklärt.
$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \mathrm{A} & \mathrm{\overline A} & \ \\\hline\mathrm{V} & 280 & \color{red}{70} & \color{red}{350} \\\hline\mathrm{\overline V}& \color{red}{120} & 30 & \color{red}{150} \\\hline\ & 400 & \color{red}{100} & 500 \end{array}$
Nun kannst du eine Vierfeldertafel mit den zugehörigen Wahrscheinlichkeiten erstellen, indem du den Wert in jeder Zelle durch die Gesamtzahl $500$ teilst. Vielleicht hast du auch direkt diese Vierfeldertafel erstellt:
$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \mathrm{A} & \mathrm{\overline A} & \ \\\hline\mathrm{V} & 0{,}56 & 0{,}14& 0{,}7\\\hline\mathrm{\overline V}& 0{,}24& 0{,}06 & 0{,}3 \\\hline\ & 0{,}8 & 0{,}2 & 1 \end{array}$
Stochastische Unabhängigkeit
Um zu überprüfen, ob zwei Ereignisse stochastisch unabhängig sind, musst du folgende Formel nachrechnen. Stimmt sie (auf beiden Seiten erhältst du dasselbe Ergebnis), dann sind sie unabhängig.
$P(A\cup V)=P(A)\cdot P(V)$
$P(A\cup V)$ kannst du in der Vierfeldertafel ablesen: $P(A\cup V)=0{,}56$
Auch die Werte für $P (A)$ und $P (V)$ kannst du ablesen und danach kannst du das Produkt ausrechnen:
$P(A)\cdot P(V)=0{,}8\cdot 0{,}7=0{,}56$
Damit stimmt die Formel und die beiden Ereignisse sind stochastisch unabhängig.
Bedeutung im Sachzusammenhang
Die Verbesserung der Symptome hängt nicht von der Wahl des Medikaments ab. Sie ist bei Hustensaft A genauso gut wie bei Hustensaft B.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Berechnen Sie $P(\overline{A}\cup V)$ . (2 BE)

3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
2.0 Ein Pharmakonzern führt eine Untersuchung über die Wirksamkeit des Grippemittels G durch. Die Zufallsgröße X gibt die Anzahl der Tage bis zur vollständigen Genesung bei Einnahme des Medikaments G an. Dabei ergibt sich mit $a,b \in \mathbb{R}$ folgende Wahrscheinlichkeitsverteilung:
2.1 Bestimmen Sie die Parameter a und b, wenn die vollständige Genesung im Durchschnitt nach 6,6 Tagen eintritt. (5 BE)

[Teilergebnis: a = 0,05]

2.2 Berechnen Sie mit den Werten von a und b aus Teilaufgabe 2.1 $P(\mu-\sigma<X<\mu+\sigma)$ . (4 BE)

2.3 Ermitteln Sie mithilfe der Werte aus Teilaufgabe 2.2 die Wahrscheinlichkeiten der folgenden Ereignisse auf 5 Nachkommastellen gerundet(6 BE):

$E_{4}$ : „Von 20 Patienten sind nach 4 Tagen genau 4 vollständig genesen.“

$E_{5}$ : „Von 100 Patienten tritt bei höchstens 30 die vollständige Genesung nach genau 7 Tagen ein.“

$E_{6}$ : „Von 50 Patienten tritt bei mindestens 10 aber weniger als 20 die vollständige Genesung nach genau 7 Tagen ein.“

Lösung zur Teilaufgabe 2.1
Hier solltest du wissen, was ein Zufallsgröße und ihr Erwartungswert ist. Außerdem solltest du in der Lage sein, ein lineares Gleichungssystem mit zwei Variablen zu lösen.
4
3.0 Der Pharmakonzern behauptet, dass bei höchstens 15% der Patienten nach der Einnahme des Medikaments G Nebenwirkungen auftreten. Der Apotheker glaubt jedoch, dass der Anteil höher ist (Gegenhypothese). Deshalb führt er eine Befragung bei 200 seiner Kunden durch, die das Medikament G genommen haben.

3.1 Geben Sie zu diesem Test die Testgröße und die Nullhypothese an und ermitteln Sie den größtmöglichen Ablehnungsbereich der Nullhypothese auf dem 5%-Niveau. (5 BE)

3.2 Welche Entscheidung legt der Test nahe, wenn bei 35 der befragten Kunden Nebenwirkungen auftreten? Erläutern Sie im Sachzusammenhang, worin bei diesem Test der Fehler 2. Art besteht. (3 BE)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle P(\overline{A}\cup V)$	$=$	$\displaystyle P(\overline{A})+P(V)-P(\overline{A}\cap V)$
	↓	Lies die Wahrscheinlichkeiten in der Vierfeldertafel ab.
	$=$	$\displaystyle 0{,}2+0{,}7-0{,}14$
	$=$	$\displaystyle 0{,}76$
	$=$	$\displaystyle 76\%$

S I

Berechnung der Teilwahrscheinlichkeiten

Hast du eine Frage oder Feedback?

E1E_1E1​: „Ein zufällig ausgewählter Kunde kauft keine Kopfschmerztabletten.“

E2E_2E2​: „Es wird Nasenspray und mindestens ein weiteres Produkt gekauft.“

E3=E1‾∪E2‾E_3=\overline{\overline{E_1} \cup E_2}E3​=E1​​∪E2​​

Möglichst einfache Formulierung

Wahrscheinlichkeit von E3E_3E3​

Hast du eine Frage oder Feedback?

Vierfeldertafel

Stochastische Unabhängigkeit

Bedeutung im Sachzusammenhang

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe 2.1

$E_{1}$ : „Ein zufällig ausgewählter Kunde kauft keine Kopfschmerztabletten.“

$E_{2}$ : „Es wird Nasenspray und mindestens ein weiteres Produkt gekauft.“

$E_3=\overline{\overline{E_1} \cup E_2}$

Wahrscheinlichkeit von $E_{3}$