Teil A

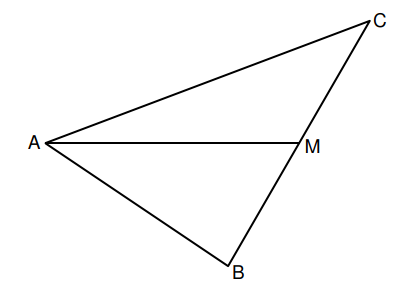
Gib den Wert für den Verzerrungsmaßstab $q$ an

Der Zeichnung entnimmt man das Maß für die Strecke $|\overline{BC}|=6\mathrm{cm}$.

Da nach Aufgabenstellung $|\overline{BC}|=9\mathrm{cm}$ beträgt, folgt für den Verzerrungsmaßstab $q$:

Der Wert für den Verzerrungsmaßstab $q$ beträgt ${\displaystyle \frac{2}{3}}$.

Ergänze die Zeichnung zur Aufgabenstellung zum Schrägbild der Pyramide $ABCS$

Die Pyramide $ABCS$ hat die Höhe $\overline{AS}$ und es gilt $\sphericalangle SCA={45}^{\circ }$.

Ergänze die zugehörigen Wahrscheinlichkeiten

In einer Urne befinden sich $25$ Kugeln gleicher Art. Fünf Kugeln sind mit dem Buchstaben $B$, alle anderen mit dem Buchstaben $A$ beschriftet.

Es gibt also $20$ Kugeln, die mit A beschriftet sind.

Wird eine $A$ Kugel gezogen, dann beträgt die Wahrscheinlichkeit beim 1. Zug $P(A)={\displaystyle \frac{20}{25}}$ und für eine $B$ Kugel beim 1. Zug $P(B)={\displaystyle \frac{5}{25}}$.

Beim 2. Zug einer $A$ Kugel sind nur noch $24$ Kugeln in der Urne, von denen $19$ $A$ Kugeln sind, sodass gilt: $P(A)={\displaystyle \frac{19}{24}}$ und $P(B)=1-{\displaystyle \frac{19}{24}}={\displaystyle \frac{5}{24}}$

Beim 3. Zug einer $A$ Kugel sind nur noch $23$ Kugeln in der Urne, von denen $18$ $A$ Kugeln sind, sodass gilt: $P(A)={\displaystyle \frac{18}{23}}$ und $P(B)=1-{\displaystyle \frac{18}{23}}={\displaystyle \frac{5}{23}}$

Siehe Abbildung:

Berechne die Wahrscheinlichkeit dafür, dass entweder beim ersten oder zweiten Ziehen eine Kugel mit dem Buchstaben $B$ gezogen wird

Betrachte das ausgefüllte Baumdiagramm.

Dann gilt für eine $B$ Kugel beim 1. Zug $P(B)={\displaystyle \frac{5}{25}}$.

Beim 2. Ziehen einer $B$ Kugel gilt dann $P(AB)={\displaystyle \frac{20}{25}}\cdot {\displaystyle \frac{5}{24}}$.

Beim ersten oder zweiten Ziehen einer $B$ Kugel erhält man dann für die Wahrscheinlichkeit:

$P=P(B)+P(AB)={\displaystyle \frac{5}{25}}+{\displaystyle \frac{20}{25}}\cdot {\displaystyle \frac{5}{24}}={\displaystyle \frac{1}{5}}+{\displaystyle \frac{1}{6}}={\displaystyle \frac{11}{30}}$

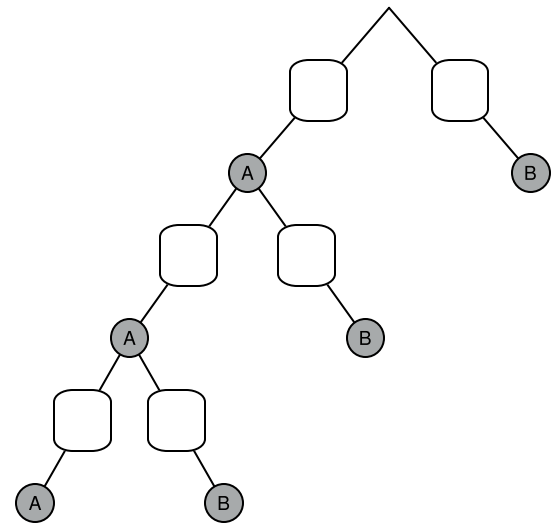
Die Wahrscheinlichkeit dafür, dass entweder beim ersten oder zweiten Ziehen eine Kugel mit dem Buchstaben $B$ gezogen wird, beträgt ${\displaystyle \frac{11}{30}}$.

Beim wievielten Ziehen erhält man mit einer Wahrscheinlichkeit von $100\%$ eine Kugel mit dem Buchstaben $B$? Begründe.

Erst wenn alle $A$ Kugeln gezogen wurden, erhält man mit einer Wahrscheinlichkeit von $100\%$ eine Kugel mit dem Buchstaben $B$.

Da es $20$ $A$ Kugeln gibt, erhält man erst beim $21.$ Zug mit Sicherheit ($100\%$) eine $B$ Kugel.

Berechne den zugehörigen Wert für $y_P$

Gegeben ist $f_1(x)={\displaystyle \frac{1}{\sqrt{x+2}}}$.

Setze $x=142$ in $f_1(x)$ ein:

$f_1(142)={\displaystyle \frac{1}{\sqrt{142+2}}}={\displaystyle \frac{1}{\sqrt{144}}}={\displaystyle \frac{1}{12}}$

$y_P$ hat den Wert ${\displaystyle \frac{1}{12}}$.

Begründe, weshalb die Funktion $f_1$ keine Nullstelle besitzt

Ein Bruch hat den Wert null, wenn der Zähler gleich null ist und der Nenner ungleich null.

Gegeben ist der Bruch ${\displaystyle \frac{1}{\sqrt{x+2}}}$ mit $x>-2$.

Der Nenner des Bruches ist für alle $x$ ungleich null, aber der Zähler ist gleich $1$ und damit ungleich null. Der Bruch kann also nicht null werden.

Die Funktion $f_1$ hat demnach keine Nullstelle.

Kreuze den passenden Vektor $\overrightarrow{v}$ an

Aus Aufgabe b) folgt, dass $f_1(x)={\displaystyle \frac{1}{\sqrt{x+2}}}>0$ ist. Der Graph von $f_1$ verläuft oberhalb der x-Achse. Damit die Funktion $f_2$ eine Nullstelle besitzt, muss die Parallelverschiebung in Richtung der negativen y-Achse erfolgen.

Dazu passt nur der Vektor $\overrightarrow{v}=\left(\begin{array}{c}0\\ -2\end{array}\right)$.