Nachtermin Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Aufgabe A1
In einem kleinen Supermarkt werden vier verschiedene Milchersatz-Produkte und zwei
verschiedene Milch-Produkte angeboten. Das Baumdiagramm zeigt Ergebnisse einer
Umfrage zum bevorzugten Milch- bzw. Milchersatzkonsum:
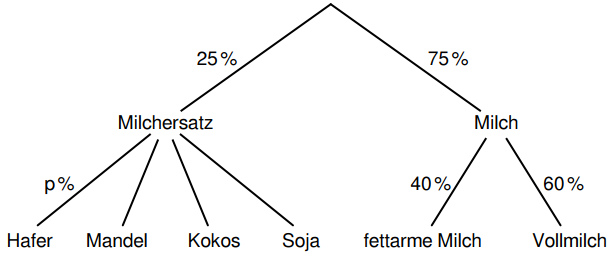
Ermitteln Sie rechnerisch die Wahrscheinlichkeit, mit der eine unter den Befragten
zufällig ausgewählte Person bevorzugt fettarme Milch konsumiert. (1,5 P)
aller Befragten gaben an, dass sie bevorzugt Hafer-Milchersatz konsumieren.
Berechnen Sie den zugehörigen Wert für . (2 P)
- 2
Aufgabe A2
Das folgende, vollständige Baumdiagramm zeigt einen Zufallsversuch zum Ziehen von
farbigen Kugeln aus einem Gefäß.
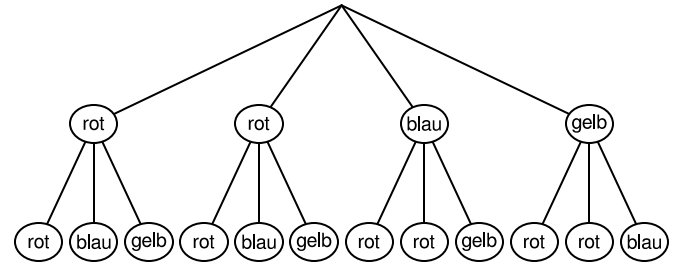
Beschreiben Sie den im Baumdiagramm aus der Aufgabenstellung dargestellten Zufallsversuch. (2 P)
Geben Sie die Wahrscheinlichkeit dafür an, dass man beim einmaligen Durchführen
des Zufallsversuchs eine blaue und eine gelbe Kugel erhält. (1 P)
- 3
Aufgabe A 3
Gegeben ist die Funktion mit der Gleichung .
Geben Sie die Gleichungen der Asymptoten des Graphen zu an. (1 P)
Der Graph der Funktion wird durch Parallelverschiebung mit einem der folgenden
Vektoren auf den Graphen der Funktion mit der Gleichung abgebildet.
Kreuzen Sie den passenden Vektor an. (1 P)

- 4
Aufgabe A4
Die untenstehende Skizze zeigt das Viereck mit der Diagonale .
Es gilt: ; ; ; ; .
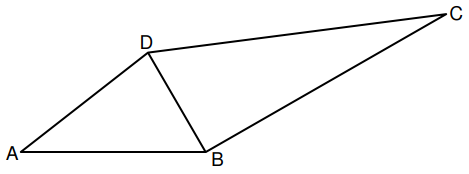
Zeigen Sie rechnerisch, dass das Dreieck rechtwinklig ist. (1,5 P)
Berechnen Sie die Länge der Strecke . (2 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

