Die Diagonalen teilen das Rechteck in vier Dreiecke.
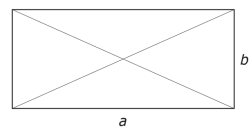
Kreuze die richtige Aussage an. \1P.
Alle vier Dreiecke...
Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt.
serlo.orgDieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt.
→ Was bedeutet das?