Teil A: Wahlpflichtteil - lernen mit Serlo!

Aufgabe 3

Gegeben sind der Punkt $P (0 | 0 | 3)$ sowie die Geraden $g : \vec{x} = \vec{O P} + t \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array}), t \in ℝ$ , und $h : \vec{x} = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array}), r \in ℝ$ .

Zeigen Sie, dass sich die Geraden $g$ und $h$ schneiden, und geben Sie die Koordinaten des Schnittpunktes $S$ an. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung zwischen zwei Geraden
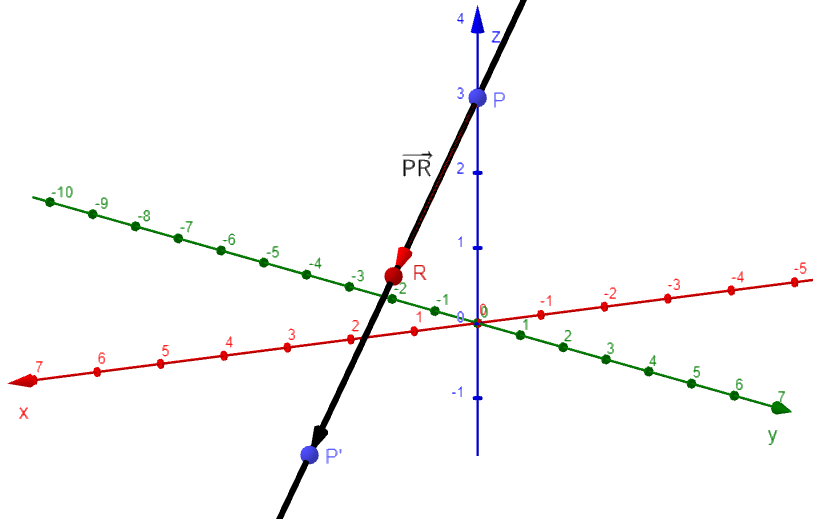
Zeige, dass sich die Geraden $g$ und $h$ schneiden
Gegeben sind $P (0 | 0 | 3)$ und $g : \vec{x} = \vec{O P} + t \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array})$ sowie $h : \vec{x} = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array})$ .
Setze $P$ in $g$ ein $\Rightarrow g : \vec{x} = (\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) + t \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array})$ .
Für Schnittpunkt setze $g = h$ :
$(\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) + t \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array}) = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array})$
$\Rightarrow (\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) - (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array}) = t \cdot (\begin{array}{c} - 2 \\ - 1 \\ 2 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array})$
$\Rightarrow (\begin{array}{c} - 4 \\ - 2 \\ 4 \end{array}) = t \cdot (\begin{array}{c} - 2 \\ - 1 \\ 2 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array})$
Aus Gleichung $II$ folgt: $- 2 = - t \Rightarrow t = 2$
$t = 2$ eingesetzt in $I$ folgt: $- 4 = 2 \cdot (- 2) + r \Rightarrow r = 0$
$t = 2$ und $r = 0$ eingesetzt in $III$ folgt: $4 = 2 \cdot 2 + 0 \cdot 2 ✓$
Das Gleichungssystem hat somit die Lösung $t = 2$ und $r = 0$ , d.h. die Geraden schneiden sich.
Gib die Koordinaten des Schnittpunktes $S$ an
Setze $r = 0$ in $h$ ein, dann erhält man die Koordinaten des Schnittpunktes.
$\vec{x_{S}} = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array}) + 0 \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array}) = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array})$
Die Geraden $g$ und $h$ schneiden sich im Punkt $S (4 | 2 | - 1)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Setze $P$ in $g$ ein.
Für Schnittpunkt setze $g = h$ und löse das Gleichungssystem.
Teil 2
Setze eine gefundene Lösung in die zugehörende Geradengleichung ein, dann erhält man die Koordinaten des Schnittpunktes.
Der Punkt $R (2 | 1 | 1)$ liegt auf der Gerade $g$ .
Bestimmen Sie die Koordinaten eines Punktes $P^{'} \neq P$ , der auf der Gerade $g$ liegt und den gleichen Abstand vom Punkt $R$ hat wie der Punkt $P$ . (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung eines Punktes an einer Geraden
Bestimme die Koordinaten eines Punktes $P^{'} \neq P$ , der auf der Gerade $g$ liegt und den gleichen Abstand vom Punkt $R$ hat wie der Punkt $P$
Gegeben sind $g : \vec{x} = (\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) + t \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array})$ und der Punkt $R (2 | 1 | 1)$ , der auf der Geraden $g$ liegt.
Berechne $\vec{P R} = \vec{O R} - \vec{O P} = (\begin{array}{c} 2 \\ 1 \\ 1 \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) = (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array})$

$\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P R} = (\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) + 2 \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array}) = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array})$ , also hat der Punkt $P^{'}$ die Koordinaten $P^{'} (4 | 2 | - 1)$ .
Die folgende Abbildung dient nur zur Veranschaulichung. Sie ist nicht in der Aufgabenstellung gefordert.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $\vec{P R}$ .
Dann ist $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P R}$ .

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das?

Aufgabe 3

Zeige, dass sich die Geraden g und h schneiden

Gib die Koordinaten des Schnittpunktes S an

Hast du eine Frage oder Feedback?

Bestimme die Koordinaten eines Punktes P′≠P, der auf der Gerade g liegt und den gleichen Abstand vom Punkt R hat wie der Punkt P

Hast du eine Frage oder Feedback?

Zeige, dass sich die Geraden $g$ und $h$ schneiden

Gib die Koordinaten des Schnittpunktes $S$ an

Bestimme die Koordinaten eines Punktes $P^{'} \neq P$ , der auf der Gerade $g$ liegt und den gleichen Abstand vom Punkt $R$ hat wie der Punkt $P$