Teil A: Wahlpflichtteil

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Abbildung 1 zeigt den Graphen $G_{f}$ einer in $ℝ$ definierten Funktion $f$ .
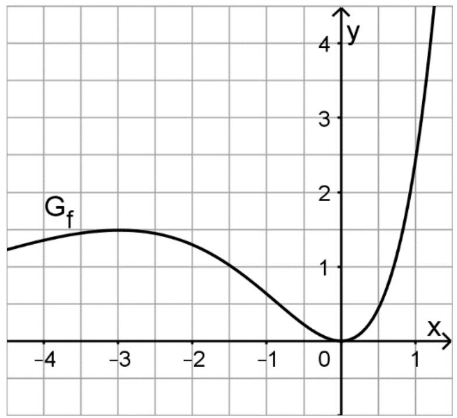
Abbildung 1
1. Bestimmen Sie grafisch den Wert des Integrals $\int_{- 3}^{- 1.5} f (x) d x$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Bestimme grafisch den Wert des Integrals $\int_{- 3}^{- 1.5} f (x) d x$
  Man zählt die Kästchen zwischen dem Graphen von $f$ und der x-Achse im Bereich von $- 3$ bis $- 1,5$ . Es sind etwa $8$ Kästchen.
  $4$ Kästchen ergeben eine Einheit, d.h. der Wert des Integrals $\int_{- 3}^{- 1,5} f (x) d x$ ist etwa $2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Zähle die Kästchen zwischen dem Graphen von $f$ und der x-Achse im Bereich von $- 3$ bis $- 1,5$ .
2. Beschreiben Sie, wie der Graph der in $ℝ$ definierten Funktion $u$ mit $u (x) = - f (x) + 2$ aus $G_{f}$ erzeugt werden kann.
  Geben Sie die Koordinaten des Hochpunktes des Graphen von $u$ an. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Transformationen von Funktionen
  Beschreibe, wie der Graph der in $ℝ$ definierten Funktion $u$ mit $𝑢 (𝑥) = - 𝑓 (𝑥) + 2$ aus $𝐺_{𝑓}$ erzeugt werden kann
  $f (x) \overset{\overset{}{Spiegelung an der x-Achse}}{\to} - f (x) \overset{\overset{}{Verschiebung um 2 in positive y-Richtung}}{\to} - f (x) + 2$
  Gib die Koordinaten des Hochpunkts des Graphen von $𝑢$ an
  Wird der Graph an der x-Achse gespiegelt, dann wird der Hochpunkt $(- 3 | 1,5)$ zum Tiefpunkt und der Tiefpunkt $(0 | 0)$ wird zum Hochpunkt.
  Nun muss der Graph noch um $2$ in positive y-Richtung verschoben werden, sodass der Hochpunkt nun die Koordinaten $(0 | 2)$ hat.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  $- f (x)$ entspricht einer Spiegelung an der x-Achse. $+ 2$ verschiebt den Graphen um 2 nach oben.
  Teil 2
  Spiegele den Graphen an der x-Achse und verschiebe ihn um $2$ nach oben. Dann kann man die Koordinaten des Hochpunkts ablesen.
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Gegeben sind die in $ℝ$ definierten Funktionen $g$ mit $g (x) = 2 \cdot e^{x} - 2$ und $h$ mit $h (x) = e^{x} + 1$ .
Abbildung 2 zeigt ihre Graphen.
Abbildung 2
1. Die erste Ableitungsfunktion von $g$ wird mit $g^{'}$ bezeichnet.
  Berechnen Sie $g^{'} (0)$ und veranschaulichen Sie in Abbildung 2, wie man diesen Wert grafisch ermitteln kann. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung und Steigungswinkel
  Berechne $g^{'} (0)$
  Gegeben ist $g (x) = 2 \cdot e^{x} - 2$ .
  $g^{'} (x) = 2 \cdot e^{x} \Rightarrow g^{'} (0) = 2 \cdot e^{0} = 2$
  Die Ableitung von $g (x)$ an der Stelle $x = 0$ hat den Wert $2$ .
  Veranschauliche in Abbildung 2, wie man diesen Wert grafisch ermitteln kann
  Abbildung 2
  Zeichne im Punkt $(0 | 0)$ die Tangente an den Graphen von $g$ . Zeichne ein Steigungsdreieck ein und lies die Steigung ab.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Berechne $g^{'} (0)$ .
  Teil 2
  Zeichne im Punkt $(0 | 0)$ die Tangente an den Graphen von $g$ .
  Zeichne ein Steigungsdreieck ein und lies die Steigung ab.
2. Beurteilen Sie die folgende Aussage:
  Es gibt eine Verschiebung in $y$ -Richtung, durch die der Graph von $h$ aus dem Graphen von $g$ erzeugt werden kann. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
  Beurteile die folgende Aussage: Es gibt eine Verschiebung in $y$ -Richtung, durch die der Graph von $h$ aus dem Graphen von $g$ erzeugt werden kann
  Die Aussage ist falsch, da die Steigungen der Graphen von $g$ und $h$ an der Stelle $x = 0$ nicht übereinstimmen:
  $h^{'} (x) = e^{x}$ , also ist $h^{'} (0) = e^{0} = 1 \neq 2 = g^{'} (0)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte die Steigungen der beiden Graphen an der Stelle $x = 0$ .
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
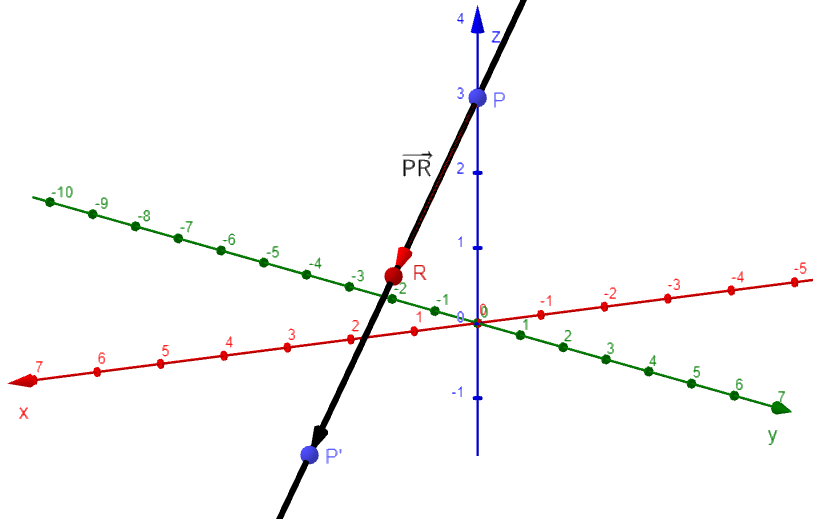
Gegeben sind der Punkt $P (0 | 0 | 3)$ sowie die Geraden $g : \vec{x} = \vec{O P} + t \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array}), t \in ℝ$ , und $h : \vec{x} = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array}), r \in ℝ$ .
1. Zeigen Sie, dass sich die Geraden $g$ und $h$ schneiden, und geben Sie die Koordinaten des Schnittpunktes $S$ an. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung zwischen zwei Geraden
  Zeige, dass sich die Geraden $g$ und $h$ schneiden
  Gegeben sind $P (0 | 0 | 3)$ und $g : \vec{x} = \vec{O P} + t \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array})$ sowie $h : \vec{x} = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array})$ .
  Setze $P$ in $g$ ein $\Rightarrow g : \vec{x} = (\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) + t \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array})$ .
  Für Schnittpunkt setze $g = h$ :
  $(\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) + t \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array}) = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array})$
  $\Rightarrow (\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) - (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array}) = t \cdot (\begin{array}{c} - 2 \\ - 1 \\ 2 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array})$
  $\Rightarrow (\begin{array}{c} - 4 \\ - 2 \\ 4 \end{array}) = t \cdot (\begin{array}{c} - 2 \\ - 1 \\ 2 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array})$
  Aus Gleichung $II$ folgt: $- 2 = - t \Rightarrow t = 2$
  $t = 2$ eingesetzt in $I$ folgt: $- 4 = 2 \cdot (- 2) + r \Rightarrow r = 0$
  $t = 2$ und $r = 0$ eingesetzt in $III$ folgt: $4 = 2 \cdot 2 + 0 \cdot 2 ✓$
  Das Gleichungssystem hat somit die Lösung $t = 2$ und $r = 0$ , d.h. die Geraden schneiden sich.
  Gib die Koordinaten des Schnittpunktes $S$ an
  Setze $r = 0$ in $h$ ein, dann erhält man die Koordinaten des Schnittpunktes.
  $\vec{x_{S}} = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array}) + 0 \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array}) = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array})$
  Die Geraden $g$ und $h$ schneiden sich im Punkt $S (4 | 2 | - 1)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Setze $P$ in $g$ ein.
  Für Schnittpunkt setze $g = h$ und löse das Gleichungssystem.
  Teil 2
  Setze eine gefundene Lösung in die zugehörende Geradengleichung ein, dann erhält man die Koordinaten des Schnittpunktes.
2. Der Punkt $R (2 | 1 | 1)$ liegt auf der Gerade $g$ .
  Bestimmen Sie die Koordinaten eines Punktes $P^{'} \neq P$ , der auf der Gerade $g$ liegt und den gleichen Abstand vom Punkt $R$ hat wie der Punkt $P$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung eines Punktes an einer Geraden
  Bestimme die Koordinaten eines Punktes $P^{'} \neq P$ , der auf der Gerade $g$ liegt und den gleichen Abstand vom Punkt $R$ hat wie der Punkt $P$
  Gegeben sind $g : \vec{x} = (\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) + t \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array})$ und der Punkt $R (2 | 1 | 1)$ , der auf der Geraden $g$ liegt.
  Berechne $\vec{P R} = \vec{O R} - \vec{O P} = (\begin{array}{c} 2 \\ 1 \\ 1 \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) = (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array})$
  
  $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P R} = (\begin{array}{c} 0 \\ 0 \\ 3 \end{array}) + 2 \cdot (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array}) = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array})$ , also hat der Punkt $P^{'}$ die Koordinaten $P^{'} (4 | 2 | - 1)$ .
  Die folgende Abbildung dient nur zur Veranschaulichung. Sie ist nicht in der Aufgabenstellung gefordert.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $\vec{P R}$ .
  Dann ist $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P R}$ .
4
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 4
Die Punkte $A (1 | 1 | 0), B (4 | 1 | 0)$ , $E (1 | 1 | 4)$ und $H (1 | 7 | 4)$ sind Eckpunkte des in Abbildung 3 dargestellten Quaders $A B C D E F G H$ .
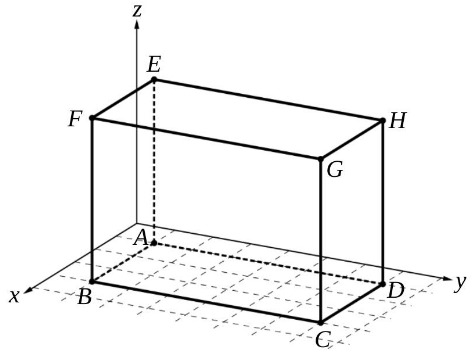
Abbildung 3
1. Geben Sie die Koordinaten des Punktes $G$ an. (1 P)
  
  Gib die Koordinaten des Punktes $G$ an
  $G$ hat dieselbe $x$ -Koordinate wie $B$ , dieselbe $y$ -Koordinate wie $H$ und dieselbe $z$ -Koordinaten wie $H$ .
  Die Koordinaten des Punktes $G$ lauten: $G (4 | 7 | 4)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überlege Dir anhand der gegebenen Koordinaten, welche Koordinaten der Punkt $G$ hat.
2. Der Quader wird parallel zu einer Gerade so verschoben, dass sich der Schnittpunkt seiner Raumdiagonalen im Koordinatenursprung befindet.
  Dabei entsteht der Quader $A^{'} B^{'} C^{'} D^{'} E^{'} F^{'} G^{'} H^{'}$ .
  Ermitteln Sie die Koordinaten des Punktes $H^{'}$ . (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung zwischen zwei Geraden
  Ermittle die Koordinaten des Punktes $H^{'}$
  Für die Koordinatenermittlung von $H^{'}$ wird der Schnittpunkt der beiden Raumdiagonalen des Quaders benötigt.
  Dieser Schnittpunkt $S$ ist der Mittelpunkt der Strecke $B H$ .
  $\vec{O S} = \frac{1}{2} \cdot (\vec{O B} + \vec{O H}) = \frac{1}{2} \cdot ((\begin{array}{c} 4 \\ 1 \\ 0 \end{array}) + (\begin{array}{c} 1 \\ 7 \\ 4 \end{array})) = \frac{1}{2} \cdot (\begin{array}{c} 5 \\ 8 \\ 4 \end{array}) = (\begin{array}{c} 2,5 \\ 4 \\ 2 \end{array})$
  Somit gilt: $S (2,5 | 4 | 2)$ .
  Der Quader wird so verschoben, dass sich der Schnittpunkt seiner Raumdiagonalen $S$ im Koordinatenursprung befindet.
  $\Rightarrow \vec{O H^{'}} = \vec{O H} - \vec{O S} = (\begin{array}{c} 1 \\ 7 \\ 4 \end{array}) - (\begin{array}{c} 2,5 \\ 4 \\ 2 \end{array}) = (\begin{array}{c} - 1,5 \\ 3 \\ 2 \end{array})$
  Die Koordinaten des Punkts $H^{'}$ lauten $(- 1,5 | 3 | 2)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Für die Koordinatenermittlung von $H^{'}$ wird der Schnittpunkt der beiden Raumdiagonalen des Quaders benötigt. Dieser Schnittpunkt $S$ ist der Mittelpunkt der Strecke $B H$ . Berechne $S$ .
  Der Quader wird so verschoben, dass sich der Schnittpunkt seiner Raumdiagonalen $S$ im Koordinatenursprung befindet.
  $\vec{O H^{'}} = \vec{O H} - \vec{O S}$
3. Geben Sie einen Eckpunkt des Quaders $A^{'} B^{'} C^{'} D^{'} E^{'} F^{'} G^{'} H^{'}$ an, der nur positive Koordinaten hat. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quader
  Gib einen Eckpunkt des Quaders $A^{'} B^{'} C^{'} D^{'} E^{'} F^{'} G^{'} H^{'}$ an, der nur positive Koordinaten hat
  Der Punkt $G$ des Quaders wird bei der Verschiebung auf den Punkt $S$ geschoben. $S$ hat die Koordinaten $(2,5 | 4 | 2)$ . Somit hat $G^{'}$ nun die Koordinaten von $S$ , die alle positiv sind.
  Der Punkt $G^{'} (2,5 | 4 | 2)$ ist der gesuchte Eckpunkt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Punkt $S$ hat z.B. nur positive Koordinaten. Überlege Dir, welcher Punkt bei der Verschiebung des Quaders auf $S$ fällt.
5
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 5
In einem Spielwarengeschäft erhält jedes Kind im Rahmen einer Werbeaktion einen kleinen, blickdicht verpackten Ball. Die Wahrscheinlichkeit dafür, dass dieser Ball eine Glitzerfärbung hat, beträgt $40 %$ .
1. Zeigen Sie, dass die Wahrscheinlichkeit dafür, dass in einer Gruppe von drei Kindern jedes Kind einen Ball mit Glitzerfärbung erhält, kleiner als $10 %$ ist. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Zeige, die Wahrscheinlichkeit dafür, dass in einer Gruppe von drei Kindern jedes Kind einen Ball mit Glitzerfärbung erhält, ist kleiner als $10 %$
  Gegeben ist $p_{Glitzer} = 0,4$ .
  Gesucht ist die Wahrscheinlichkeit $P (X = 3)$ :
  $P (X = 3) = {0,4}^{3} = 0,064 < 0,1$
  Damit ist $P (X = 3) < 10 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $P (X = 3)$ mit $p = 0,4$ und $n = 3$ .
2. Beschreiben Sie in diesem Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term ${(\frac{3}{5})}^{4} + 4 \cdot {(\frac{3}{5})}^{3} \cdot \frac{2}{5}$ berechnet werden kann. Geben Sie dieses Ereignis an. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Beschreiben Sie in diesem Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term ${(\frac{3}{5})}^{4} + 4 \cdot {(\frac{3}{5})}^{3} \cdot \frac{2}{5}$ berechnet werden kann. Geben Sie dieses Ereignis an
  Gegeben ist $p_{Glitzer} = 0,4 = \frac{2}{5}$ .
  Dann ist die Gegenwahrscheinlichkeit $p_{Glitzer} = 1 - \frac{2}{5} = \frac{3}{5}$
  Der 1. Term ${(\frac{3}{5})}^{4}$ ist die Wahrscheinlichkeit dafür, dass von $4$ Kindern keines einen Ball mit Glitzerfärbung erhält.
  Der 2. Term ${(\frac{3}{5})}^{4}$ ist die Wahrscheinlichkeit dafür, dass von $4$ Kindern eines einen Ball mit Glitzerfärbung erhält.
  Zufallsexperiment: Vier Kinder erhalten jeweils einen Ball.
  Ereignis: Mindestens drei dieser Bälle haben keine Glitzerfärbung.
  (Oder: Höchstens ein Kind erhält einen Ball mit Glitzerfärbung.)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Untersuche getrennt die beiden Teile des angegebenen Terms.
6
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 6
Die Zufallsgröße $X$ ist binomialverteilt mit den Parametern $n$ und $p = \frac{1}{4}$ .
1. Für die Standardabweichung $σ$ von $X$ gilt: $σ = \sqrt{3}$ .
  Berechnen Sie $n$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Standardabweichung
  Berechne $n$
  Gegeben: $σ = \sqrt{3}$ und $p = \frac{1}{4}$ .
  Es ist $σ = \sqrt{n \cdot p \cdot (1 - p)} = \sqrt{n \cdot \frac{1}{4} \cdot \frac{3}{4}} = \sqrt{3} \overset{\overset{}{quadrieren}}{\to} n \cdot \frac{3}{16} = 3 \Rightarrow n = 16$
  Das gesuchte $n$ ist gleich $16$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es ist $σ = \sqrt{n \cdot p \cdot (1 - p)}$ .
  Setze die gegebenen Werte $σ$ und $p$ ein und löse nach $n$ auf.
2. Die folgende Abbildung 4 zeigt die Werte $P_{n; \frac{1}{4}} (X = k)$ der Zufallsgröße $X$ im Bereich von $k = 3$ bis $k = 5$ ; Abbildung 5 zeigt kumulierte Werte $P_{n; \frac{1}{4}} (X \leq k)$ der Zufallsgröße $X$ im Bereich von $k = 3$ bis $k = 5$ .
  In Abbildung 5 fehlt der Wert $P_{n; \frac{1}{4}} (X \leq 4)$ . (3 P)
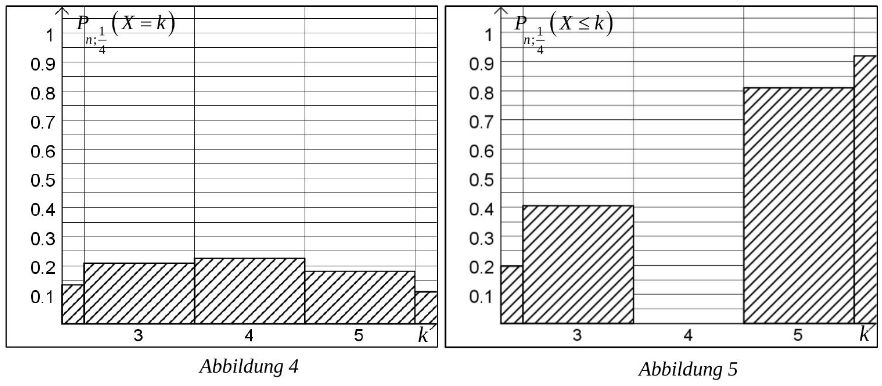
  Ermitteln Sie näherungsweise $P_{n; \frac{1}{4}} (X \leq 4)$ und vervollständigen Sie Abbildung 5.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kumulierte Wahrscheinlichkeit
  Ermittele näherungsweise $P_{n; \frac{1}{4}} (X \leq 4)$
  Abbildung 4 entnimmt man $P_{n; \frac{1}{4}} (X = 4) \approx 0,23$ .
  Abbildung 5 entnimmt man $P_{n; \frac{1}{4}} (X \leq 3) \approx 0,40$ .
  Dann folgt für $P_{n; \frac{1}{4}} (X \leq 4) = P_{n; \frac{1}{4}} (X \leq 3) + P_{n; \frac{1}{4}} (X = 4) \approx 0,40 + 0,23 = 0,63$ .
  Näherungsweise beträgt $P_{n; \frac{1}{4}} (X \leq 4) \approx 0,63$ .
  Vervollständige Abbildung 5
  Der Wert $0,63$ wird für $P_{n; \frac{1}{4}} (X \leq 4)$ in die Abbildung 5 eingezeichnet.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Abbildung 4 entnimmt man $P_{n; \frac{1}{4}} (X = 4)$ und Abbildung 5 entnimmt man $P_{n; \frac{1}{4}} (X \leq 3)$ .
  Dann gilt: $P_{n; \frac{1}{4}} (X \leq 4) = P_{n; \frac{1}{4}} (X \leq 3) + P_{n; \frac{1}{4}} (X = 4)$ .
  Teil 2
  Der berechnete Wert wird für $P_{n; \frac{1}{4}} (X \leq 4)$ in die Abbildung 5 eingezeichnet.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Teil A: Wahlpflichtteil

Aufgabe 1

Bestimme grafisch den Wert des Integrals ∫−3−1.5f(x)dx

Hast du eine Frage oder Feedback?

Beschreibe, wie der Graph der in ℝ definierten Funktion u mit 𝑢(𝑥)=−𝑓(𝑥)+2 aus 𝐺𝑓 erzeugt werden kann

Gib die Koordinaten des Hochpunkts des Graphen von 𝑢 an

Hast du eine Frage oder Feedback?

Aufgabe 2

Berechne g′(0)

Veranschauliche in Abbildung 2, wie man diesen Wert grafisch ermitteln kann

Hast du eine Frage oder Feedback?

Beurteile die folgende Aussage: Es gibt eine Verschiebung in y-Richtung, durch die der Graph von h aus dem Graphen von g erzeugt werden kann

Hast du eine Frage oder Feedback?

Aufgabe 3

Zeige, dass sich die Geraden g und h schneiden

Gib die Koordinaten des Schnittpunktes S an

Hast du eine Frage oder Feedback?

Bestimme die Koordinaten eines Punktes P′≠P, der auf der Gerade g liegt und den gleichen Abstand vom Punkt R hat wie der Punkt P

Hast du eine Frage oder Feedback?

Aufgabe 4

Gib die Koordinaten des Punktes G an

Hast du eine Frage oder Feedback?

Ermittle die Koordinaten des Punktes H′

Hast du eine Frage oder Feedback?

Gib einen Eckpunkt des Quaders A′B′C′D′E′F′G′H′ an, der nur positive Koordinaten hat

Hast du eine Frage oder Feedback?

Aufgabe 5

Zeige, die Wahrscheinlichkeit dafür, dass in einer Gruppe von drei Kindern jedes Kind einen Ball mit Glitzerfärbung erhält, ist kleiner als 10%

Hast du eine Frage oder Feedback?

Beschreiben Sie in diesem Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term (35)4+4⋅(35)3⋅25 berechnet werden kann. Geben Sie dieses Ereignis an

Hast du eine Frage oder Feedback?

Aufgabe 6

Berechne n

Hast du eine Frage oder Feedback?

Ermittele näherungsweise Pn;14(X≤4)

Vervollständige Abbildung 5

Hast du eine Frage oder Feedback?

Bestimme grafisch den Wert des Integrals $\int_{- 3}^{- 1.5} f (x) d x$

Beschreibe, wie der Graph der in $ℝ$ definierten Funktion $u$ mit $𝑢 (𝑥) = - 𝑓 (𝑥) + 2$ aus $𝐺_{𝑓}$ erzeugt werden kann

Gib die Koordinaten des Hochpunkts des Graphen von $𝑢$ an

Berechne $g^{'} (0)$

Beurteile die folgende Aussage: Es gibt eine Verschiebung in $y$ -Richtung, durch die der Graph von $h$ aus dem Graphen von $g$ erzeugt werden kann

Zeige, dass sich die Geraden $g$ und $h$ schneiden

Gib die Koordinaten des Schnittpunktes $S$ an

Bestimme die Koordinaten eines Punktes $P^{'} \neq P$ , der auf der Gerade $g$ liegt und den gleichen Abstand vom Punkt $R$ hat wie der Punkt $P$

Gib die Koordinaten des Punktes $G$ an

Ermittle die Koordinaten des Punktes $H^{'}$

Gib einen Eckpunkt des Quaders $A^{'} B^{'} C^{'} D^{'} E^{'} F^{'} G^{'} H^{'}$ an, der nur positive Koordinaten hat

Zeige, die Wahrscheinlichkeit dafür, dass in einer Gruppe von drei Kindern jedes Kind einen Ball mit Glitzerfärbung erhält, ist kleiner als $10 %$

Beschreiben Sie in diesem Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term ${(\frac{3}{5})}^{4} + 4 \cdot {(\frac{3}{5})}^{3} \cdot \frac{2}{5}$ berechnet werden kann. Geben Sie dieses Ereignis an

Berechne $n$

Ermittele näherungsweise $P_{n; \frac{1}{4}} (X \leq 4)$