Wahlteil
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Aufgaben und Lösungen der Mathe Realschulprüfung 2024 vom Wahlteil.
Taschenrechner und Formelsammlung sind in diesem Prüfungsteil erlaubt.
Du musst zwei Aufgaben aus dem Wahlteil wählen und lösen. Die anderen Wahlaufgaben musst du nicht bearbeiten.
- 1
Eine Firma stellt die abgebildete Praline her. Alle Längen sind in angegeben.

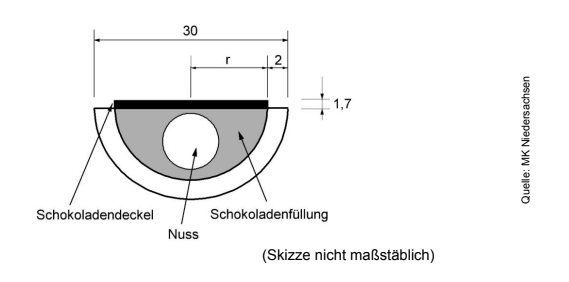
Auf der Praline befindet sich ein zylinderförmiger Schokoladendeckel.
Berechne das Volumen des Schokoladendeckels.
[ 2 Pkte ]
Das Volumen der kugelförmigen Nuss beträgt .
Berechne den Durchmesser der Nuss.
[ 3 Pkte ]
Berechne das Volumen der Schokoladenfüllung.
[ 3 Pkte ]
Eine Firma stellt eine Sonderedition dieser Praline mit doppeltem Radius her. Die Nuss bleibt dabei gleich groß.
Jörn behauptet: „Dann ist auch das Volumen der Schokoladenfüllung doppelt so groß.“
Hat Jörn recht? Begründe deine Entscheidung.
[ 2 Pkte ]
- 2
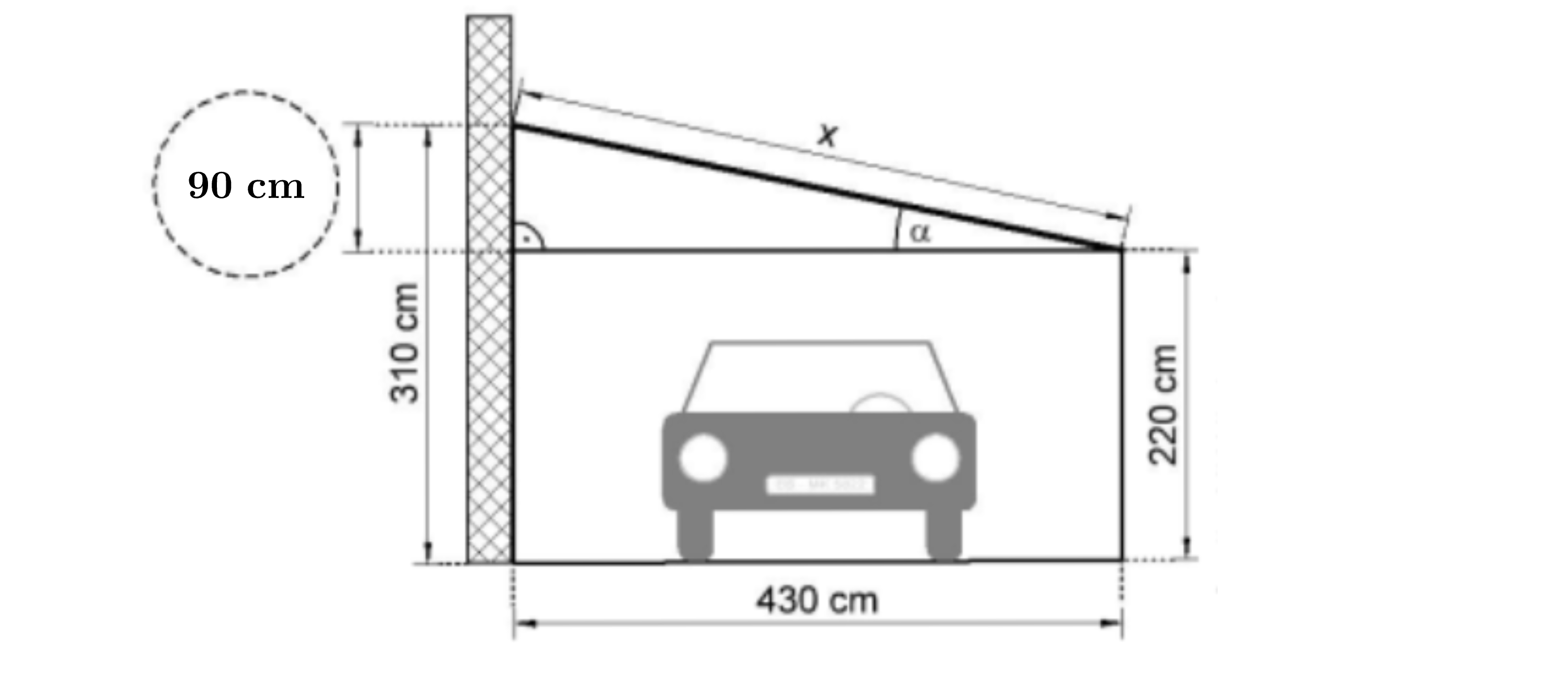
Die Abbildung zeigt einen Carport.
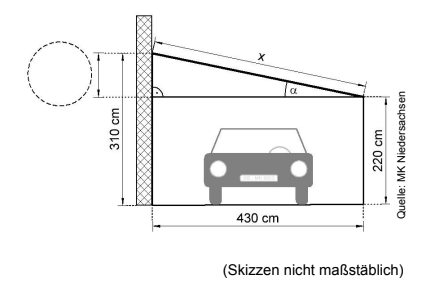
Ergänze das fehlende Maß in der Skizze.
[ 1 Pkt ]
Berechne die Länge eines Dachbalkens.
[ 3 Pkte ]
Berechne den Winkel .
[ 2 Pkte ]
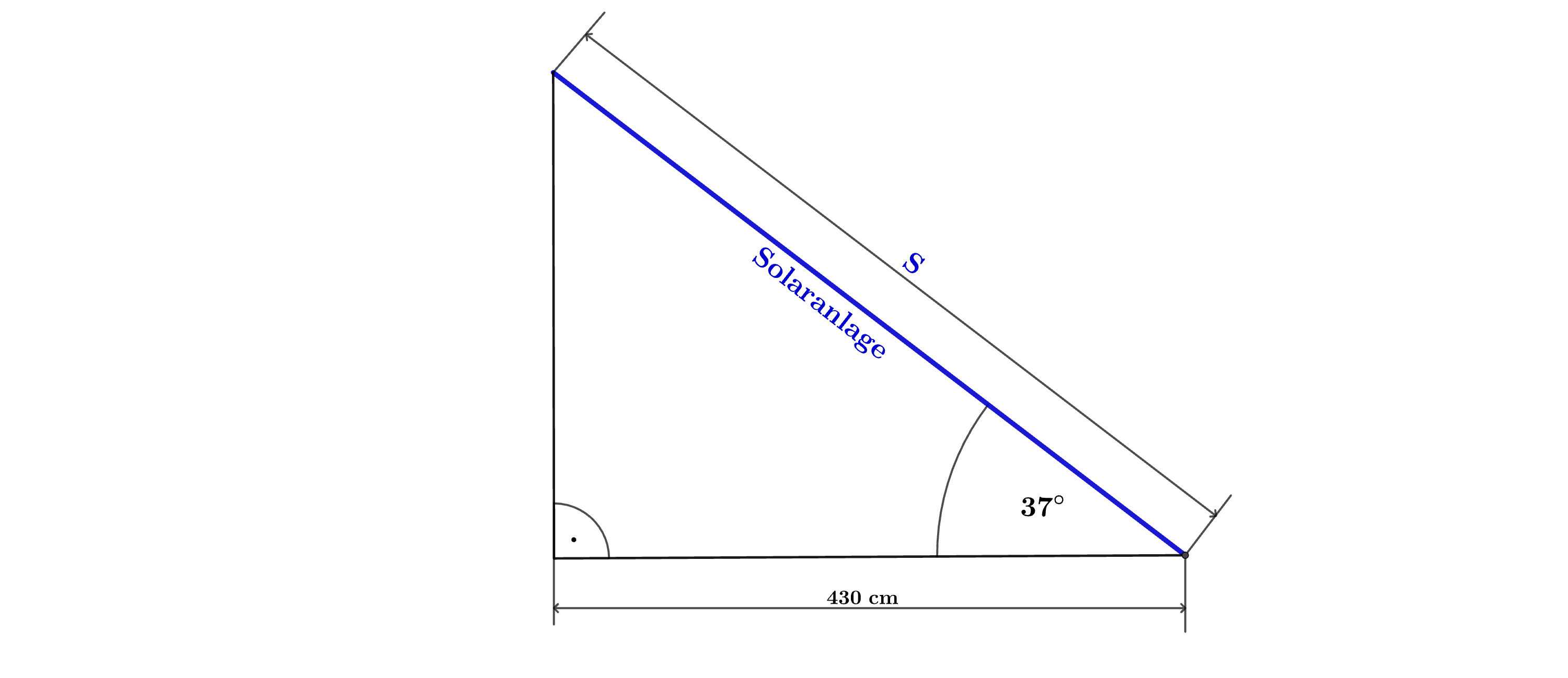
Auf das Dach des Carports soll eine Solaranlage mit einem Winkel von gebaut werden. Tilo möchte die maximale Länge der Solaranlage bestimmen und hat eine Skizze
angefertigt.
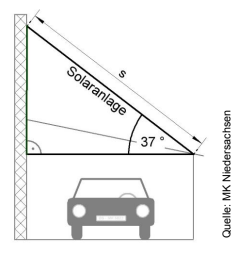
Zeichne dafür ein geeignetes rechtwinkliges Dreieck und bestimme die maximale Länge der Solaranlage.
(Wähle für in der Wirklichkeit in der Zeichnung.)
[ 3 Pkte ]
Tilo behauptet: „Wenn der -Winkel halbiert wird, dann halbiert sich auch die maximale Länge der Solaranlage.“
Zeige zeichnerisch oder rechnerisch, dass Tilos Behauptung falsch ist.
[ 1 Pkt ]
- 3
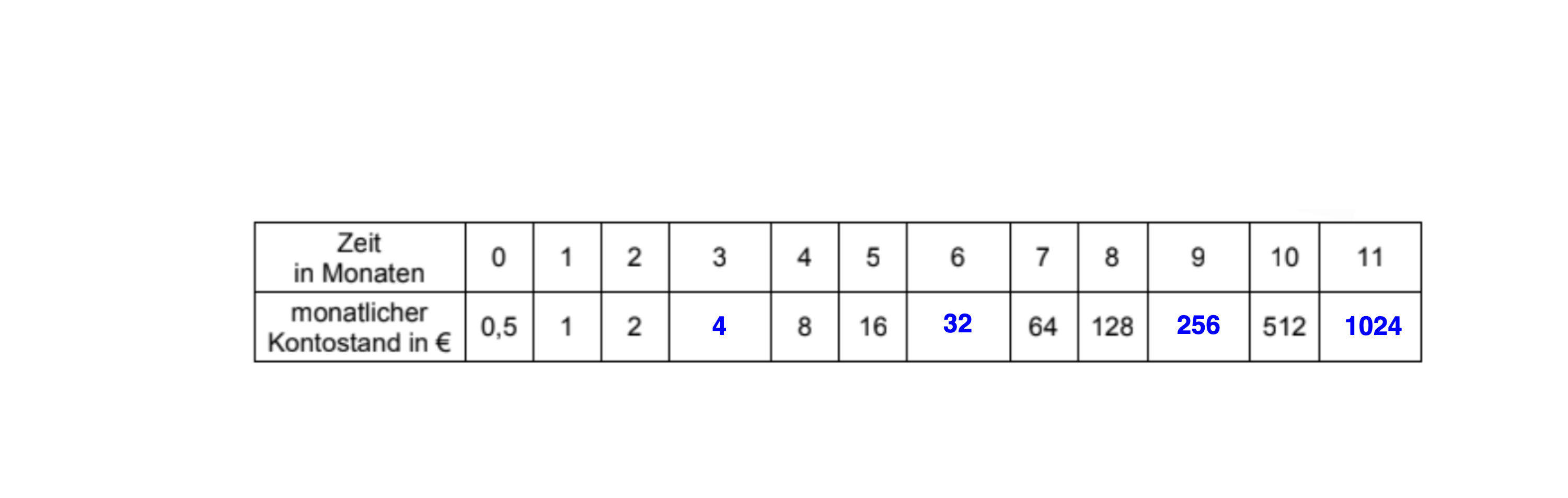
Paul möchte sich ein neues Fahrrad kaufen. Sein Vater macht ein besonderes Angebot: „Ich lege ein Konto an und verdoppele jeden Monat den Kontostand.“

Ergänze die Wertetabelle.

[ 2 Pkte ]
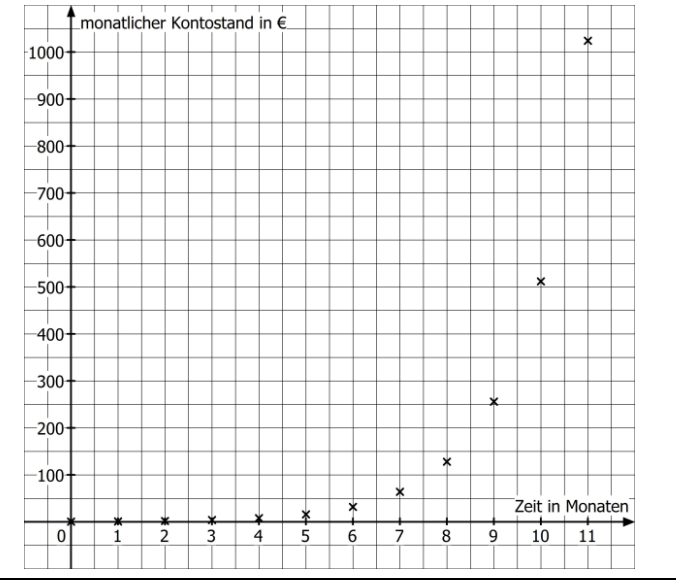
Zeichne ein Koordinatensystem und trage die Werte ein.
(Wähle bei der -Achse 1 für 1 Monat und bei der -Achse für €.)
[ 3 Pkte ]
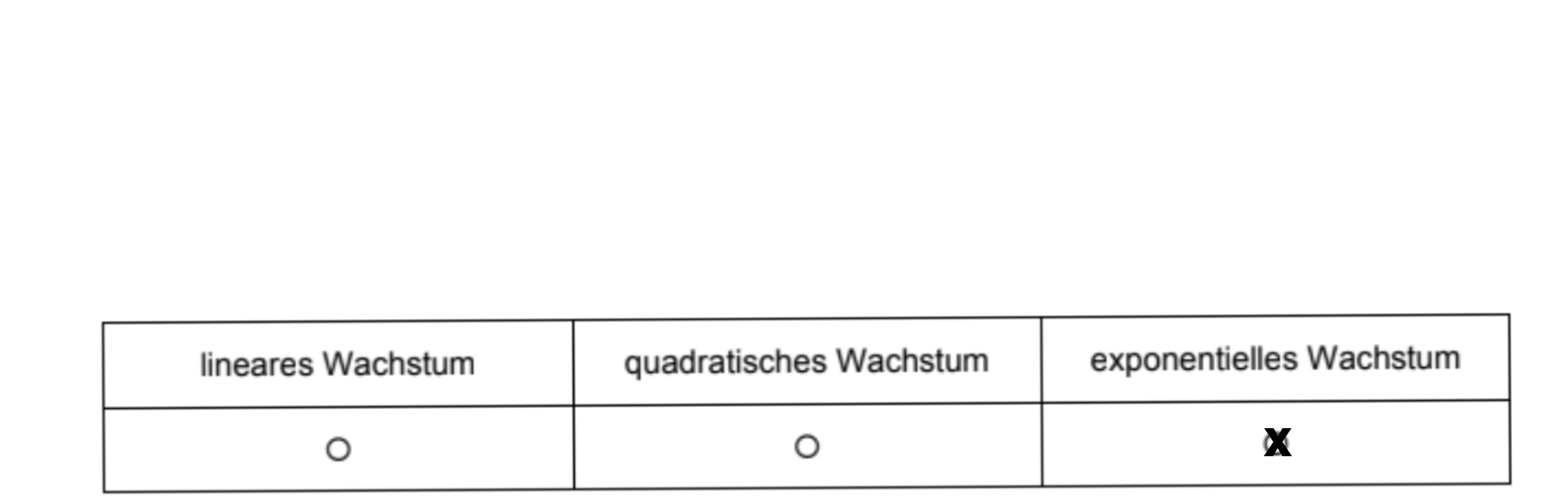
Kreuze die Art des Wachstumsprozesses an.

[ 1 Pkt ]
Von seinen Großeltern erhält Paul folgendes Angebot.

Paul behauptet: „Dann habe ich nach vier Monaten schon € von meinen Großeltern bekommen.“
Zeige, dass Paul recht hat.
[ 1 Pkt ]
Der Geldbetrag von den Großeltern wächst linear an.
Gib die Funktionsgleichung in der Form an.
[ 2 Pkte ]
Paul behauptet: „Nach 11 Monaten ist der Geldbetrag von meinem Vater größer.“
Begründe, dass Pauls Behauptung richtig ist.
[ 1 Pkt ]
- 4
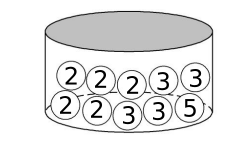
In einer Schale sind Kugeln mit den Ziffern 2, 3 und 5.
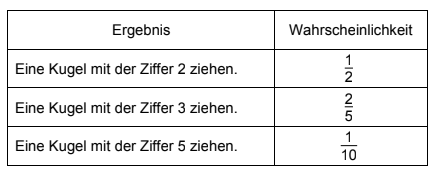
Es wurden noch keine Kugeln gezogen. Beschrifte die Kugeln in der Schale.
[ 2 Pkte ]
Osman zieht nacheinander zwei Kugeln aus der Schale. Er zeichnet ein Baumdiagramm.
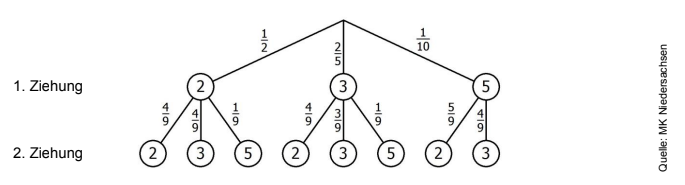
Hat Osman die erste gezogene Kugel zurückgelegt? Begründe deine Entscheidung.
[ 2 Pkte ]
Osman berechnet die Wahrscheinlichkeit für ein Ereignis:
Beschreibe ein passendes Ereignis.
[ 1 Pkt ]
Osman gewinnt, wenn die Ziffern auf zwei Kugeln die Summe 5 ergeben.
Berechne die Wahrscheinlichkeit.
[ 3 Pkte ]
Alle Kugeln werden wieder in die Schale zurückgelegt. Osman zieht aus der Schale eine Kugel und legt sie nach dem ersten Ziehen wieder zurück.
Zeichne ein passendes Baumdiagramm für zwei Ziehungen.
[ 2 Pkte ]
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?