Aufgabe 1
In einem kartesischen Koordinatensystem sind die Punkte , und sowie der Punkt gegeben.
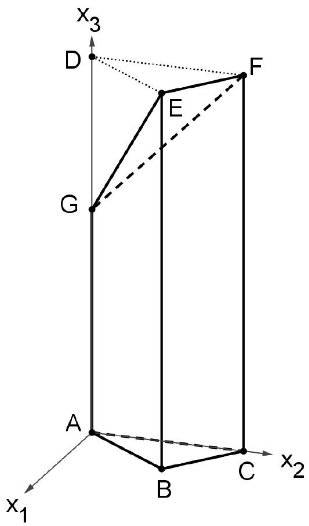
Abbildung
Der in der Abbildung dargestellte Körper ist ein dreieckiges Prisma.
Geben Sie die Koordinaten des Punktes an. (1 P)
Für ist der Punkt gegeben.
Zeigen Sie, dass das Dreieck für jedes im Punkt rechtwinklig ist. (3 P)
Der Punkt soll die Strecke im Verhältnis teilen.
Geben Sie ein so an, dass diese Bedingung erfüllt. (1 P)
Für gilt .
Berechnen Sie den Flächeninhalt des Dreiecks und das Volumen des Prismas . (3 P)
Zur Kontrolle: .
