Aufgaben zur linearen Unabhängigkeit

Hier findest du Aufgaben zur linearen Unabhängigkeit. Lerne, Vektoren auf ihre lineare Unabhängigkeit zu überprüfen und dessen Bedeutung!

1
Bestimme die Skalare, sodass der Vektor $\overrightarrow u$ eine Linearkombination der Vektoren $\overrightarrow{v_i}$ ist.
1. $\displaystyle\overrightarrow u=\begin{pmatrix}7\\12\end{pmatrix}, \overrightarrow{v_1}=\begin{pmatrix}-5\\-5\end{pmatrix},\overrightarrow{v_2}=\begin{pmatrix}-1\\\frac23\end{pmatrix}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linearkombination
  Zu bestimmen sind die Skalare $a,b\in\mathbb{R}$ , sodass gilt
  $\overrightarrow{u}=a\cdot\overrightarrow{v_1}+b\cdot\overrightarrow{v_2}$ .
  Setze die gegebenen Vektoren ein.
  $\displaystyle\begin{pmatrix}7\\12\end{pmatrix}=a\cdot\begin{pmatrix}-5\\-5\end{pmatrix}+b\cdot\begin{pmatrix}-1\\\frac23\end{pmatrix}$
  Es handelt sich um ein lineares Gleichungssystem mit den Variablen $a$ und $b$ .
  $\def\arraystretch{1.25} \begin{array}{cccccc}\text{I}&7&=&-5\cdot a&+&(-1)\cdot b\\\text{II}&12& =&-5\cdot a&+&\frac23\cdot b\end{array}$
  $\Rightarrow a=-2, \;b=3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $\displaystyle\overrightarrow u=\begin{pmatrix}1\\1\end{pmatrix}, \overrightarrow{v_1}=\begin{pmatrix}1\\2\end{pmatrix},\overrightarrow{v_2}=\begin{pmatrix}2\\1\end{pmatrix}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linearkombination
  Zu bestimmen sind die Skalare $a,b∈\mathbb R$ , sodass gilt
  $\overrightarrow u=a\cdot\overrightarrow{v_1}+b\cdot\overrightarrow{v_2}$
  Setze die gegebenen Vektoren ein.
  $\begin{pmatrix}1\\1\end{pmatrix}=a\cdot\begin{pmatrix}1\\2\end{pmatrix}+b\cdot\begin{pmatrix}2\\1\end{pmatrix}$
  Es handelt sich um ein lineares Gleichungssystem mit den Variablen $a$ und $b$ .
  $\def\arraystretch{1.25} \begin{array}{cccccc}\text I & 1&=&1\cdot a&+&2\cdot b\\\text{II}&1&=&2\cdot a&+&1\cdot b\end{array}$
  $\displaystyle\Rightarrow a=\frac13,\;b=\frac13$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $\displaystyle\overrightarrow u=\begin{pmatrix}-3\\5\\6\end{pmatrix}, \overrightarrow{v_1}=\begin{pmatrix}1\\1\\0\end{pmatrix},\overrightarrow{v_2}=\begin{pmatrix}1\\1\\1\end{pmatrix},\overrightarrow{v_3}=\begin{pmatrix}1\\0\\1\end{pmatrix}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Linearkombination
  Zu bestimmen sind die Skalare $a,b,c∈\mathbb R$ , sodass gilt
  $\overrightarrow u=a\cdot\overrightarrow{v_1}+b\cdot\overrightarrow{v_2}+c\cdot\overrightarrow{v_3}$
  Setze die gegebenen Vektoren ein.
  $\begin{pmatrix}-3\\5\\6\end{pmatrix}=a\cdot\begin{pmatrix}1\\1\\0\end{pmatrix}+b\cdot\begin{pmatrix}1\\1\\1\end{pmatrix}+c\cdot\begin{pmatrix}1\\0\\1\end{pmatrix}$
  Es handelt sich um ein lineares Gleichungssystem mit den Variablen $a, b$ und $c$ .
  $\def\arraystretch{1.25} \begin{array}{ccccccc}\text I&-3&=&1\cdot a&+&1\cdot b&+&1\cdot c\\\text{II}&5&=&1\cdot a&+&1\cdot b&&\\\text{III}&6&=&&&1\cdot b&+&1\cdot c\end{array}$
  $\Rightarrow a=-9,\;b=14,\;c=-8$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Prüfe, ob die Vektoren linear unabhängig sind.

$\overrightarrow{v_1}=\begin{pmatrix}1\\0\end{pmatrix},\;\overrightarrow{v_2}=\begin{pmatrix}0\\1\end{pmatrix}$
- linear abhängig
- linear unabhängig
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Unabhängigkeit
Die Vektoren $\overrightarrow{v_1}$ und $\overrightarrow{v_2}$ sind linear unabhängig, wenn du zwei Zahlen $a,b\in\mathbb{R}$ finden kannst, sodass $a\cdot \overrightarrow{v_1}+b\cdot \overrightarrow{v_2}=\begin{pmatrix}0\\0\end{pmatrix}$ und $a$ und $b$ nicht beide gleichzeitig $0$ sind.
Setz die gegebenen Vektoren ein.
$\displaystyle a\cdot\begin{pmatrix}1\\0\end{pmatrix}+b\cdot\begin{pmatrix}0\\1\end{pmatrix}=\begin{pmatrix}0\\0\end{pmatrix}$
Es handelt sich um ein lineares Gleichungssystem mit den Variablen $a$ und $b$ .
$\def\arraystretch{1.25} \displaystyle\begin{array}{cccccc}\text{I}&1\cdot a&+&0\cdot b &=& 0\\\text{II}&0\cdot a&+&1\cdot b &=& 0\end{array}$
Löse das lineare Gleichungssystem.
$\displaystyle \text{I}\ \ \ 1\cdot a+0\cdot b$ $=$ $\displaystyle 0$
$\displaystyle a+0$ $=$ $\displaystyle 0$
$\displaystyle a$ $=$ $\displaystyle 0$
$\displaystyle \text{II}\ \ 0\cdot a+1\cdot b$ $=$ $\displaystyle 0$
$\displaystyle 0+b$ $=$ $\displaystyle 0$
$\displaystyle b$ $=$ $\displaystyle 0$
$\Rightarrow a=0, \;b=0$ . Das bedeutet, das Gleichungssystem ist nur gelöst für $a = b = 0$ und somit sind $\overrightarrow{v_1}$ und $\overrightarrow{v_2}$ linear unabhängig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$\overrightarrow{v_1}=\begin{pmatrix}-3\\2\end{pmatrix},\;\overrightarrow{v_2}=\begin{pmatrix}4{,}5\\-3\end{pmatrix}$

linear abhängig
linear unabhängig

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Unabhängigkeit

Die Vektoren $\overrightarrow{v_1}$ und $\overrightarrow{v_2}$ sind linear unabhängig, wenn du zwei Zahlen $a,b\in\mathbb{R}$ finden kannst, sodass $a\cdot \overrightarrow{v_1}+b\cdot \overrightarrow{v_2}=\begin{pmatrix}0\\0\end{pmatrix}$ und $a$ und $b$ nicht beide gleichzeitig $0$ sind.

Setz die gegebenen Vektoren ein.

$\displaystyle a\cdot\begin{pmatrix}-3\\2\end{pmatrix}+b\cdot\begin{pmatrix}4{,}5\\-3\end{pmatrix}=\begin{pmatrix}0\\0\end{pmatrix}$

Es handelt sich um ein lineares Gleichungssystem mit den Variablen $a$ und $b$ .

$\def\arraystretch{1.25} \displaystyle\begin{array}{cccccc}\text{I}&(-3)\cdot a&+&4{,}5\cdot b &=& 0\\\text{II}&2\cdot a&+&(-3)\cdot b &=& 0\end{array}$

Löse das lineare Gleichungssystem.

$\displaystyle \text{I}\ \ \left(-3\right)\cdot a+4{,}5\cdot b$	$=$	$\displaystyle 0$
$\displaystyle -3a+4{,}5b$	$=$	$\displaystyle 0$	$\displaystyle +3a$
$\displaystyle 4{,}5b$	$=$	$\displaystyle 3a$	$\displaystyle :3$
$\displaystyle a$	$=$	$\displaystyle 1{,}5b$

Setze nun $a = 1,5 b$ in $\text{II}$ ein.

$\displaystyle \text{II}\ \ 2\cdot a+\left(-3\right)\cdot b$	$=$	$\displaystyle 0$
	↓	Setze $a = 1,5 b$ ein.
$\displaystyle 2\cdot\left(1{,}5b\right)-3b$	$=$	$\displaystyle 0$
	↓	Vereinfache
$\displaystyle 3b-3b$	$=$	$\displaystyle 0$
$\displaystyle 0$	$=$	$\displaystyle 0$

Die Gleichung ist immer erfüllt. Also müssen $a$ und $b$ nur die Gleichung $a = 1,5 b$ erfüllen. Für beispielsweise $b = 1$ und $a=1{,}5\cdot1=1{,}5$ ist die Gleichung also erfüllt und somit sind $\overrightarrow{v_1}$ und $\overrightarrow{v_2}$ linear abhängig.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$\overrightarrow{v_1}=\begin{pmatrix}3\\8\\9\end{pmatrix},\;\overrightarrow{v_2}=\begin{pmatrix}4\\7\\-2\end{pmatrix},\;\overrightarrow{v_3}=\begin{pmatrix}2\\2\\2\end{pmatrix}$
- linear abhängig
- linear unabhängig
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Unabhängigkeit
Die Vektoren $\overrightarrow{v_1}$ , $\overrightarrow{v_2}$ und $\overrightarrow{v_3}$ sind linear unabhängig, wenn du drei Zahlen $a,b,c\in\mathbb{R}$ finden kannst, sodass
$a\cdot \overrightarrow{v_1}+b\cdot \overrightarrow{v_2}+c\cdot\overrightarrow{v_3}=\begin{pmatrix}0\\0\\0\end{pmatrix}$ und $a$ , $b$ und $c$ gleichzeitig $0$ sind.
Setze die gegebenen Vektoren ein.
$\displaystyle a\cdot\begin{pmatrix}3\\8\\9\end{pmatrix}+b\cdot\begin{pmatrix}4\\7\\-2\end{pmatrix}+c\cdot\begin{pmatrix}2\\2\\2\end{pmatrix}=\begin{pmatrix}0\\0\\0\end{pmatrix}$
Es handelt sich um ein lineares Gleichungssystem mit den Variablen $a$ , $b$ und $c$ .
$\def\arraystretch{1.25} \displaystyle\begin{array}{cccccccc}\text{(I)}&3\cdot a&+&4\cdot b &+& 2\cdot c&=& 0\\\text{(II)}&8\cdot a&+&7\cdot b &+& 2\cdot c&=& 0 \\\text{(III)}&9\cdot a&-& 2\cdot b&+&2\cdot c&=&0\end{array}$
Löse das lineare Gleichungssystem zum Beispiel mit dem Additionsverfahren.
Rechne:
$\text{(II)}-\text{(I)}\;\Rightarrow\;\mathrm{(I')}:\;\;\;5\cdot a + 3\cdot b = 0$
$\text{(III)}-\text{(II)}\Rightarrow\;\mathrm{(II')}:\;\; \;\; \;\;a -9\cdot b = 0$
Rechne: $3\cdot\mathrm{( I')}+\mathrm{(II')}\;\Rightarrow\;16\cdot a=0\;\Rightarrow\;a=0$
Setze $a = 0$ in $\mathrm{( I')}$ ein $\;\Rightarrow\;5\cdot 0+3\cdot b=0\;\Rightarrow\;b=0$
Setze $a = 0$ und $b = 0$ in $\mathrm{(I)}$ ein $\;\Rightarrow\;3\cdot 0+4\cdot 0+2\cdot c=0\;\Rightarrow\;c=0$
Es ist also $a=0,\,b=0,\,c=0$ . Das bedeutet, das Gleichungssystem wird nur gelöst für $a = b = c = 0$ und somit sind $\overrightarrow{v_1}$ , $\overrightarrow{v_2}$ und $\overrightarrow{v_3}$ linear unabhängig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

3
Prüfe rechnerisch, ob die drei Vektoren komplanar sind.
1. $\vec a =\begin{pmatrix} 1\\0\\-1\end{pmatrix}, \vec b=\begin{pmatrix}0\\3\\0\end{pmatrix}, \vec c=\begin{pmatrix}2\\1\\2\end{pmatrix}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare (Un)abhängigkeit
  Sind die Vektoren linear unabhängig, so kann man zum Beispiel den Vektor $\vec c$ eindeutig durch $\vec a$ und $\vec b$ darstellen:
  $\lambda\cdot \vec a+\mu\cdot \vec b=\vec c$
  Daraus entsteht ein Gleichungssystem mit drei Gleichungen und zwei Unbekannten:
  $\def\arraystretch{1.25} \begin{array}{rrl} I)&\lambda &=2\\ II)&3\mu&=1\\ III)& -\lambda&=2 \end{array}$
  Die erste und die dritte Gleichung liefern unterschiedliche Lösungen für $\lambda$ . Dadurch hat das Gleichungssystem keine eindeutige Lösung.
  Die Vektoren sind also linear unabhängig und nicht komplanar.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $\vec a =\begin{pmatrix} 1\\2\\-3\end{pmatrix}, \vec b=\begin{pmatrix}-1\\-1\\2\end{pmatrix}, \vec c=\begin{pmatrix}0\\4\\-4\end{pmatrix}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare (Un)abhängigkeit
  Sind die Vektoren linear unabhängig, so kann man zum Beispiel den Vektor $\vec c$ eindeutig durch $\vec a$ und $\vec b$ darstellen:
  $\lambda\cdot \vec a+\mu\cdot \vec b=\vec c$
  Daraus entsteht ein Gleichungssystem mit drei Gleichungen und zwei Unbekannten:
  $\def\arraystretch{1.25} \begin{array}{rrl} I)&\lambda-\mu &=0\\ II)&2\lambda-\mu&=4\\ III)& -3\lambda+2\mu&=-4 \end{array}$
  Forme die erste Gleichung um:
  $I) \lambda=\mu$
  Setze in II ein:
  $\def\arraystretch{1.25} \begin{array}{rrll} II)&2\mu-\mu&=4\\ &\mu&=4 \end{array}$
  Und die erste Gleichung liefert
  $I) \lambda =4$
  Da es sich um ein überbestimmtes System handelt, musst du zur Probe noch in die III. Gleichung einsetzen:
  $\def\arraystretch{1.25} \begin{array}{rrll}III)&-3\cdot4+2\cdot 4&=-4\\&-4&=-4\end{array}$
  Die Gleichung III liefert eine wahre Aussage. Somit hat das System eine eindeutige Lösung und die drei Vektoren sind linear abhängig und somit komplanar.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $\vec a =\begin{pmatrix} 1\\-2\\2\end{pmatrix}, \vec b=\begin{pmatrix}-3\\6\\-6\end{pmatrix}, \vec c=\begin{pmatrix}2\\4\\-4\end{pmatrix}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare (Un)abhängigkeit
  Da die Vektoren $\vec a$ und $\vec b$ parallel sind, kann man nicht wie bei den letzten Aufgaben $\lambda\cdot \vec a+\mu\cdot \vec b=\vec c$ untersuchen.
  Alternativ prüfst du $\lambda\cdot \vec{c}+\mu\cdot \vec b=\vec a$
  Daraus entsteht erneut ein Gleichungssystem mit drei Gleichungen und zwei Unbekannten:
  $\def\arraystretch{1.25} \begin{array}{rrl} I)&2\lambda-3\mu &=1\\ II)&4\lambda+6\mu&=-2\\ III)& -4\lambda-6\mu&=2 \end{array}$
  Forme z.B. die erste Gleichung um: $I) 2\lambda =1+3\mu$
  Setze in die II. Gleichung ein:
  $\def\arraystretch{1.25} \begin{array}{rrl} II)&2\cdot2\lambda-3\mu&=1\\ &2(1+3\mu)-3\mu&=1\\ &2+6\mu-3\mu&=1&|-2\\ &3\mu&=-1&|:3\\ &\mu&=-\frac 1 3 \end{array}$
  Setze das Ergebnis in Gleichung I ein:
  $I)2\lambda=1+3\cdot\left(-\frac 1 3\right)\\ I)\lambda=0$
  Setze in Gleichung III ein:
  $III) -4\cdot 0-6\cdot \left(-\frac 1 3\right)=2\\ III)2=2$
  Das System hat also eine eindeutige Lösung und somit sind die drei Vektoren komplanar.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Zeige, dass sich der Vektor $\begin{pmatrix} 9\\18\end{pmatrix}$ auf unendlich viele Arten als Linearkombination der Vektoren $\begin{pmatrix}1\\2\end{pmatrix}$ und $\begin{pmatrix} 3\\6\end{pmatrix}$ darstellen lässt und deute das Ergebnis geometrisch.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Linearkombination
Als Linearkombination darstellen bedeutet, dass du Zahlen $r_{1}, r_{2}$ finden musst, so dass:
$r_1\cdot \begin{pmatrix} 1\\2\end{pmatrix}+r_2\cdot \begin{pmatrix} 3\\6\end{pmatrix}=\begin{pmatrix}9\\18\end{pmatrix}$
Daraus entsteht ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten:
$\def\arraystretch{1.25} \begin{array}{rc} I)&r_1+3r_2=9\\ II)&2r_1+6r_2=18 \end{array}$
Wenn du die zweite Gleichung halbierst, erhältst du erneut die erste Gleichung:
$\displaystyle 2r_1+6r_2$ $=$ $\displaystyle 18$ $\displaystyle :2$
$\displaystyle r_1+3r_2$ $=$ $\displaystyle 9$
Somit handelt es sich um ein unterbestimmtes System mit unendlich vielen Lösungen.
Forme die erste Gleichung um, um die Lösungsmenge in Abhängigkeit von $r_{2}$ anzugeben:
$I) r_{1} = 9 - 3 r_{2}$
Für $r_{2} = 2$ ergibt sich zum Beispiel $r_1=9-3\cdot 2=3$ .
Für $r_{2} = 1$ ergibt sich folglich $r_1=9-3\cdot 1=6$
geometrische Interpretation
Bei genauerem Hinsehen solltest du erkennen, dass alle drei Vektoren kollinear sind, also paarweise parallel. Sie liegen also auf einer gemeinsamen Geraden.
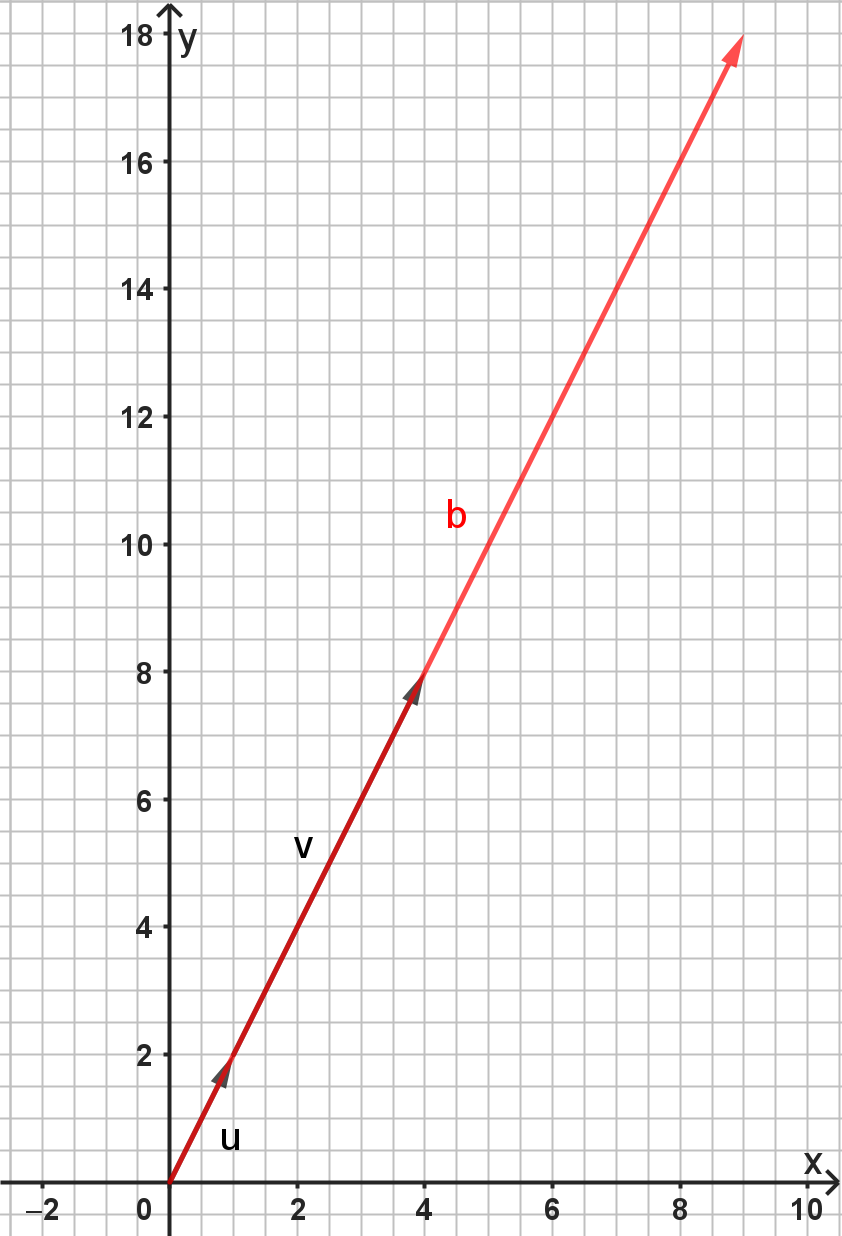
Einen Vektor $\vec v$ als Linearkombination von $\vec a$ und $\vec b$ darzustellen, bedeutet, Zahlen zu finden, mit denen $\vec a$ und $\vec b$ multipliziert werden können, so dass der Vektor $\vec v$ entsteht.
Zeige, dass es unendlich viele solche Zahlen gibt.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \text{I}\ \ \ 1\cdot a+0\cdot b$	$=$	$\displaystyle 0$
$\displaystyle a+0$	$=$	$\displaystyle 0$
$\displaystyle a$	$=$	$\displaystyle 0$

$\displaystyle \text{II}\ \ 0\cdot a+1\cdot b$	$=$	$\displaystyle 0$
$\displaystyle 0+b$	$=$	$\displaystyle 0$
$\displaystyle b$	$=$	$\displaystyle 0$

$\displaystyle 2r_1+6r_2$	$=$	$\displaystyle 18$	$\displaystyle :2$
$\displaystyle r_1+3r_2$	$=$	$\displaystyle 9$

Aufgaben zur linearen Unabhängigkeit

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

geometrische Interpretation