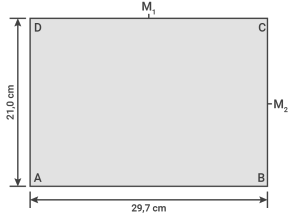
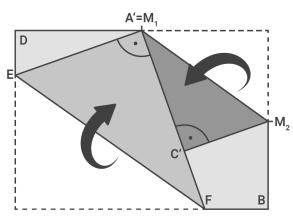
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Dreiecks
Berechne die Flächeninhalte des Dreiecks und des Vierecks .
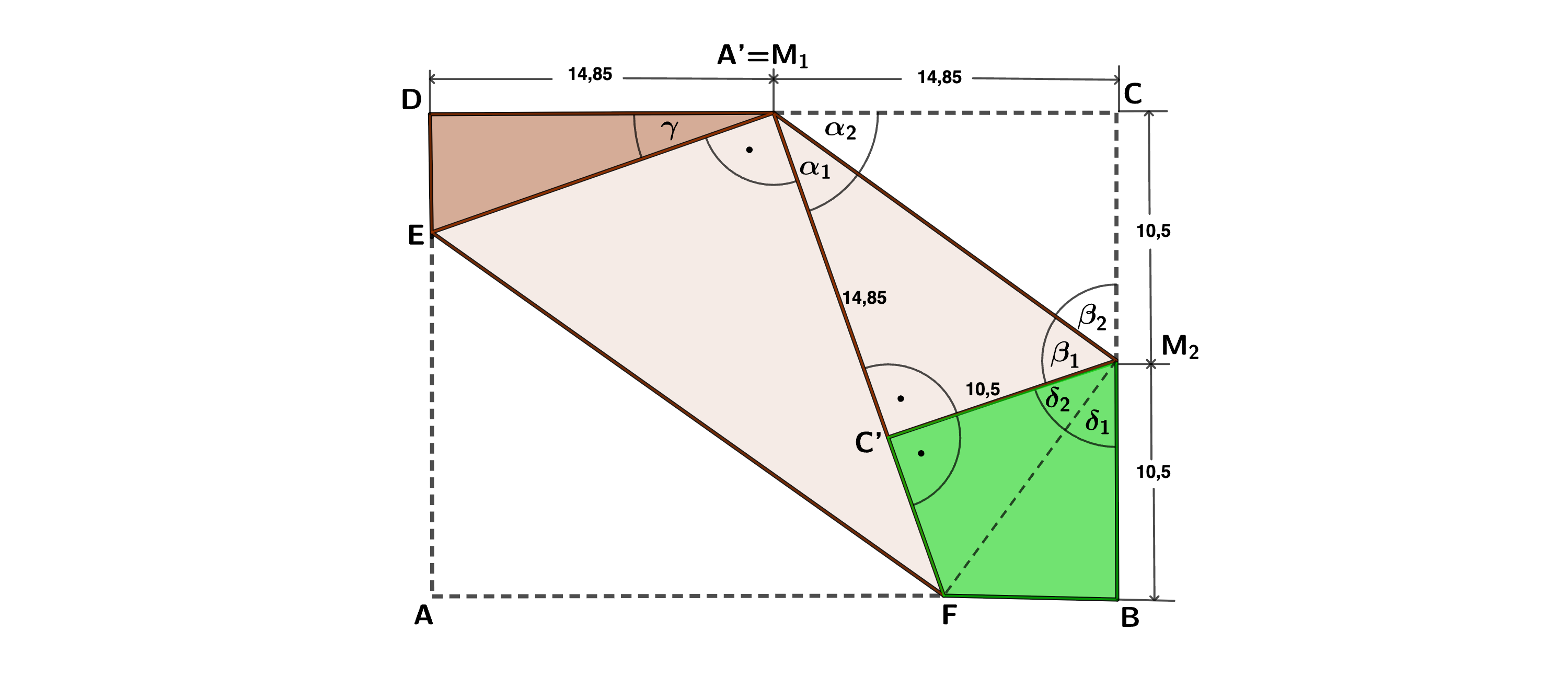
Bild 3
Berechnen des Flächeninhaltes des Dreiecks .
Bestimmen des Winkels mithilfe des Tangens.
Das Dreieck ist ein rechtwinkliges Dreieck, im rechtwinkligem Dreieck gilt:
Angewandt auf das Dreieck :
Bestimmen des Winkels .
wegen Kongruenz der Dreiecke und .
Bestimmen der Seite :
Berechnen des Flächeninhalts des Dreiecks
Der Flächeninhalt des Dreiecks beträgt: .
Satz des Pythagoras angewandt auf das Dreieck :
auflösen der Klammer |
| ↓ |
| | | |
| ↓ | subtrahieren |
| | | |
| ↓ | subtrahieren |
| | | |
| ↓ | dividieren |
| | | |
Der Flächeninhalt des Dreiecks beträgt: .
Berechnen des Flächeninhaltes des Vierecks .
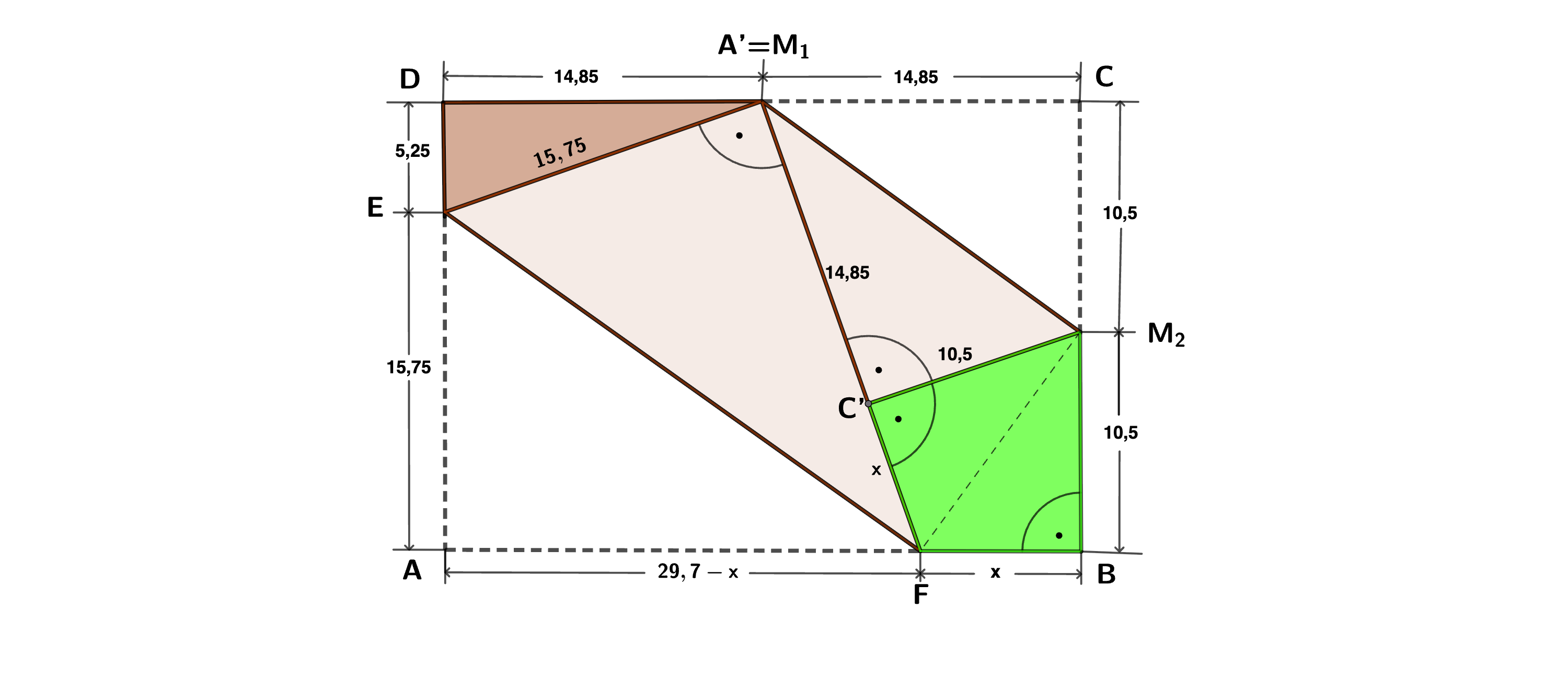
Bild 4
Das grüne Viereck kann in die rechtwinkligen Dreiecke und zerlegt werden, diese beiden Dreiecke sind kongruent, siehe Bild 4.
Berechnen des Flächeninhaltes des Dreiecks .
Berechnen von mithilfe des Satzes des Pythagoras.
Die Dreiecke und sind kongruent.
Satz des Pythagoras angewandt auf das Dreieck :
Satz des Pythagoras angewandt auf das Dreieck :
gleichsetzen |
| ↓ |
| | | |
| ↓ | subtrahieren |
| | | |
| ↓ | Klammern auflösen |
| | | |
| ↓ | subtrahieren |
| | | |
| ↓ | subtrahieren |
| | | |
| ↓ | dividieren |
| | | |
Der Flächeninhalt des Vierecks ist dann:
Hast du eine Frage oder Feedback?
Kommentiere hier 👇