Analysis, Teil B, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Gegeben ist die in $ℝ$ definierte Funktion $f : x \mapsto 5 x \cdot e^{- x}$ .
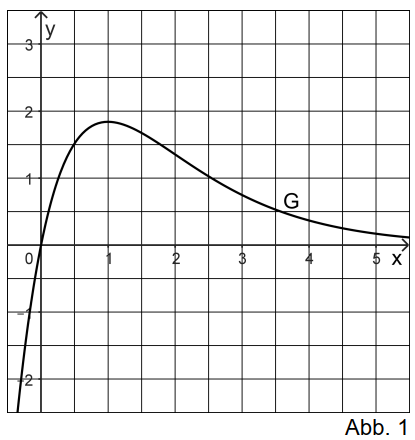
Abbildung 1 zeigt den Graphen $G$ von $f$ .
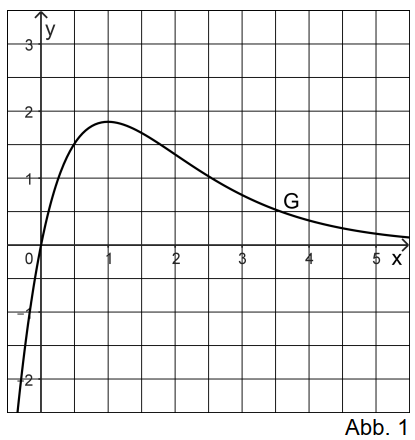
1. $G$ hat genau einen Extrempunkt.
  Berechnen Sie die Koordinaten des Extrempunkts von $G$ .
  $(zur Kontrolle : (1 | \frac{5}{e}) ⁣)$ (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremum
  Berechne die Koordinaten des Extrempunkts von $G$
  Die notwendige Bedingung für ein Extremum ist $f^{'} (x) = 0$ .
  Bilde mithilfe der Produkt- und Kettenregel die 1. Ableitung:
  $f^{'} (x) = 5 (1 \cdot e^{- x} + x \cdot e^{- x} \cdot (- 1)) = 5 \cdot (1 - x) \cdot e^{- x}$
  $f^{'} (x) = 0 \Rightarrow 0 = 5 \cdot (1 - x) \cdot e^{- x}$
  Weil $e^{- x} \neq 0$ für alle $x \in ℝ$ folgt mit dem Satz vom Nullprodukt:
  $1 - x = 0 \Rightarrow x = 1$
  $f (1) = 5 \cdot 1 \cdot e^{- 1} = \frac{5}{e}$
  Die Koordinaten des Extrempunkts von $G$ sind $(1 | \frac{5}{e})$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die notwendige Bedingung für ein Extremum ist $f^{'} (x) = 0$ .
  Bilde mithilfe der Produkt- und Kettenregel die 1. Ableitung und löse die Gleichung: $f^{'} (x) = 0 \Rightarrow x_{E}$
  Berechne noch $f (x_{E})$ und gibt die Koordinaten $(x_{E} | f (x_{E}))$ des Extrempunktes an.
2. Die Tangente $t$ an $G$ in dessen Wendepunkt hat die Gleichung $y = - \frac{5}{e^{2}} x + \frac{20}{e^{2}}$ .
  Ermitteln Sie eine Gleichung der Geraden, die den Extrempunkt von $G$ enthält und senkrecht zu $t$ verläuft. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Ermittle eine Gleichung der Geraden, die den Extrempunkt von $G$ enthält und senkrecht zu $t$ verläuft
  Die Tangente $t$ an $G$ in dessen Wendepunkt hat die Gleichung $y = - \frac{5}{e^{2}} x + \frac{20}{e^{2}}$ .
  $\Rightarrow m_{W} = - \frac{5}{e^{2}} \Rightarrow m_{g} = \frac{e^{2}}{5}$ , da $m_{W} \cdot m_{g} = - 1$
  $g : y = \frac{5}{e^{2}} \cdot x + b$
  Setze die Koordinaten $(1 | \frac{5}{e})$ des Extrempunkts von $G$ in $g$ ein.
  $\frac{5}{e} = \frac{5}{e^{2}} \cdot 1 + b \Rightarrow b = \frac{5}{e} - \frac{5}{e^{2}}$
  Die Gleichung der Geraden, die den Extrempunkt von $G$ enthält und senkrecht zu $t$ verläuft, ist $g : y = \frac{5}{e^{2}} \cdot x + \frac{5}{e} - \frac{5}{e^{2}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es ist $g : y = m_{g} \cdot x + b$ .
  Dabei ist $m_{W} \cdot m_{g} = - 1$ . Da $m_{W}$ gegeben ist, kann $m_{g}$ berechnet werden.
  Setze die Koordinaten $(1 | \frac{5}{e})$ des Extrempunkts von $G$ in $g$ ein und berechne den y-Achsenabschnitt.
3. Betrachtet wird die in $[1; + \infty [$ definierte Funktion $h$ mit $h (x) = f (x)$ .
  Begründen Sie, dass die Funktion $f$ nicht umkehrbar, die Funktion $h$ jedoch umkehrbar ist. Geben Sie den Definitions- und den Wertebereich der Umkehrfunktion von $h$ an. (6 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Umkehrfunktion
  Begründe, dass die Funktion $f$ nicht umkehrbar, die Funktion $h$ jedoch umkehrbar ist
  Aus Abbildung 1 entnimmt man, dass es zwei x-Werte gibt, für die $f (x) = 1,5$ ist. Daher ist $f$ nicht umkehrbar.
  Es ist $f^{'} (x) = 5 \cdot (1 - x) \cdot e^{- x}$ und $f^{'} (x) < 0$ in $] 1; + \infty [$ .
  Die Funktion $h$ ist umkehrbar, da $f$ im Intervall $[1; + \infty [$ streng monoton ist.
  Gib den Definitions- und den Wertebereich der Umkehrfunktion von $h$ an
  Gegeben ist $D_{h} = [1; + \infty [$ . Dann ist $W_{h^{- 1}} = [1; + \infty [$ .
  Die Koordinaten des Extrempunkts von $G$ sind $(1 | \frac{5}{e})$ $\Rightarrow y_{max} = \frac{5}{e}$
  Weiterhin gilt: $\lim_{x \to + \infty} h (x) = 0$ , dann ist $D_{h^{- 1}} =] 0; \frac{5}{e}]$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Finde zwei x-Werte gibt, die den gleichen Funktionswert $f (x)$ haben. Daher ist $f$ nicht umkehrbar.
  Es ist $\lim_{x \to + \infty} h (x) = 0$ . Zeige, dass $h$ im Intervall $[1; + \infty [$ streng monoton fallend ist.
  Teil 2
  Gegeben ist $D_{h} = [1; + \infty [$ . Dann ist $W_{h^{- 1}} = D_{h}$ .
  Die Koordinaten des Extrempunkts von $G$ sind $(1 | \frac{5}{e})$ $\Rightarrow y_{max} = \frac{5}{e}$ und $\lim_{x \to + \infty} h (x) = 0 \Rightarrow D_{h^{- 1}}$ .
4. Abbildung 2 zeigt eine Figur, die modellhaft das Wappen eines Sportvereins beschreibt. Die Begrenzungslinien der Figur werden durch einen Teil der Geraden mit der Gleichung $y = 5$ sowie durch die Kurvenstücke $H_{1}$ und $H_{2}$ beschrieben:
  $H_{1}$ entsteht, indem $G$ für $x \in [\ln 5; 5]$ an der Geraden mit der Gleichung $y = x$ gespiegelt wird.
  $H_{2}$ entsteht durch Spiegeln von $H_{1}$ an der Geraden mit der Gleichung $x = \ln 5$ .
  Der Punkt $S (\ln 5 | \ln 5)$ ist gemeinsamer Punkt von $H_{1}$ und $H_{2}$ .
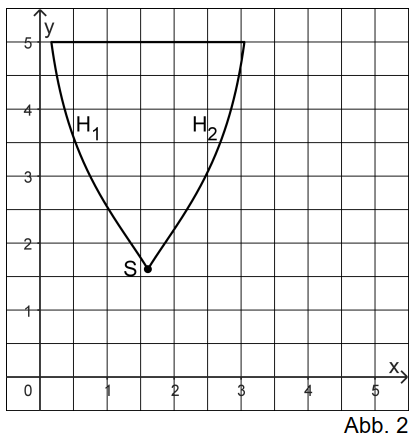
  Begründen Sie, dass mit dem Term $2 \cdot ((5 - \ln 5) \cdot \ln 5 - \int_{\ln 5}^{5} f (x) d x)$ der Flächeninhalt der Figur berechnet werden kann. (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Begründe, dass mit dem Term $2 \cdot ((5 - \ln 5) \cdot \ln 5 - \int_{\ln 5}^{5} f (x) d x)$ der Flächeninhalt der Figur berechnet werden kann
  Der Flächeninhalt des braun eingezeichneten Rechtecks ist $A = (5 - \ln 5) \cdot \ln 5$
  (Länge: $(5 - \ln 5)$ , Breite $\ln 5$ )
  Beachte, $h (x) = f (x)$ , mit $D_{h} =$ $[1; + \infty [$ .
  Dann ist $\int_{\ln 5}^{5} f (x) d x$ der Flächeninhalt, den $G$ und die Geraden $x = \ln 5$ und $x = 5$ mit der x-Achse einschließen.
  Bildet man die Differenz von $A$ und $\int_{\ln 5}^{5} f (x) d x$ , dann erhält man den Flächeninhalt der grün schraffierten Fläche.
  Spiegelt man die grün schraffierte Fläche an der Geraden $y = x$ , erhält man den Flächeninhalt der linken Hälfte des Wappens.
  Der gesamte Flächeninhalt der Figur ist dann $2 \cdot ((5 - \ln 5) \cdot \ln 5 - \int_{\ln 5}^{5} f (x) d x)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte das Viereck, das zwischen den Geraden $y = 0, y = \ln 5, x = \ln 5$ und $x = 5$ liegt. Gib seinen Flächeninhalt an $\Rightarrow A_{1}$ .
  Welchen Flächeninhalt beschreibt $A_{2} = \int_{\ln 5}^{5} f (x) d x$ ?
  Welcher Flächeninhalt ist dann die Differenz zwischen $A_{1}$ und $A_{2}$ ?
5. Die in $ℝ$ definierte Funktion $F : x \mapsto - 5 (x + 1) \cdot e^{- x}$ ist eine Stammfunktion von $f$ . Berechnen Sie mit dem Term aus Aufgabe 1d den Flächeninhalt der Figur auf eine Nachkommastelle genau. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Berechne mit dem Term aus Aufgabe 1d den Flächeninhalt der Figur auf eine Nachkommastelle genau
  Gegeben ist $F (x) = - 5 (x + 1) \cdot e^{- x}$ .
  Weiterhin gilt: $A = 2 \cdot ((5 - \ln 5) \cdot \ln 5 - \int_{\ln 5}^{5} f (x) d x) = 2 \cdot ((5 - \ln 5) \cdot \ln 5 - (F (5) - F (\ln 5))$
  $F (5) = - 5 (5 + 1) \cdot e^{- 5} = - 30 \cdot e^{- 5}$
  $F (\ln 5) = - 5 (\ln 5 + 1) \cdot e^{- \ln 5} = - 5 (\ln 5 + 1) \cdot 0,2$
  Dann ist $A = 2 \cdot ((5 - \ln 5) \cdot \ln 5 - (- 30 \cdot e^{- 5} - (- 5 (\ln 5 + 1) \cdot 0,2))$
  $A = 2 \cdot ((5 - \ln 5) \cdot \ln 5 + 30 \cdot e^{- 5} - 1 \cdot (\ln 5 + 1))) \approx 6,1$
  Der Flächeninhalt der Figur auf eine Nachkommastelle genau berechnet, beträgt rund $6,1 FE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $\int_{\ln 5}^{5} f (x) d x = F (5) - F (\ln 5)$ und setze in den Term $2 \cdot ((5 - \ln 5) \cdot \ln 5 - \int_{\ln 5}^{5} f (x) d x)$ ein.
2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Die Abb. 1 aus Aufgabe 1 wird hier benötigt.
Weiterhin ist bekannt: $G$ hat genau einen Extrempunkt $(1 | \frac{5}{e})$ .
Betrachtet wird die Schar der in $ℝ$ definierten Funktionen $g_{k} : x \mapsto - 5 x \cdot e^{- k x}$
mit $k \in ℝ \ {0}$ .
Abbildung 3 zeigt vier Graphen der Schar, die zu den Werten $k = - 1, k = - 0,5, k = 0,5$ und $k = 1$ gehören.
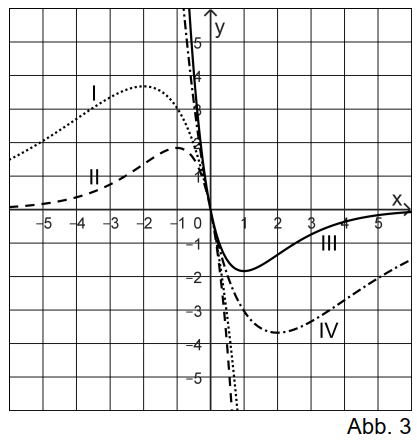
1. Der Graph III kann durch Spiegeln von $G$ (vgl. Abbildung 1) an der x-Achse erzeugt werden. Geben Sie den zugehörigen Wert von $k$ sowie die Koordinaten des
  Tiefpunkts von Graph III an.
  Ordnen Sie den drei übrigen Werten von $k$ den jeweils passenden Graphen zu. (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Transformationen
  Gib den zugehörigen Wert von $k$ sowie die Koordinaten des Tiefpunkts von Graph III an
  Graph III: Der Wert von $k$ ist $k = 1$ .
  $g_{1} (x) = - 5 x \cdot e^{- 1 x} = - f (x)$
  $\Rightarrow g_{1} (x)$ wurde durch Spiegeln von $G$ an der x-Achse erzeugt.
  $G$ hat genau einen Extrempunkt $(1 | \frac{5}{e})$ . Dann hat $G_{g_{1}}$ den $T P (1 | - \frac{5}{e})$ .
  Ordne den drei übrigen Werten von $k$ den jeweils passenden Graphen zu
  Die beiden positiven k-Werte gehören zu den Graphen im 4. Quadranten.
  Da $g_{1} (x) = - f (x)$ ist, gehört Graph III zu $k = 1$ und Graph IV zu $k = 0,5$ .
  Entsprechend gehört in 2. Quadranten der Graph I zu $k = - 0,5$ und Graph II zu $k = - 1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte $G$ aus Aufgabe 1.
  $G$ wird an der x-Achse gespiegelt.
  Welcher Graph ist es dann?
  Die beiden positiven k-Werte gehören zu den Graphen im 4. Quadranten.
  Entscheide entsprechend für den 2. Quadranten.
2. Zeigen Sie, dass $g_{k} (- x) = - g_{- k} (x)$ für alle $x \in ℝ$ gilt, und interpretieren Sie diese Gleichung mit Blick auf die Graphen der Funktionen $g_{k}$ und $g_{- k}$ . (4 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punktsymmetrie
  Zeige, dass $g_{k} (- x) = - g_{- k} (x)$ für alle $x \in ℝ$ gilt
  $- g_{- k} (x) = - (- 5 x \cdot e^{- (- k) x}) = - 5 (- x) \cdot e^{- k (- x)} = g_{k} (- x)$
  Interpretiere diese Gleichung mit Blick auf die Graphen der Funktionen $g_{k}$ und $g_{- k}$
  Die Graphen der Funktionen $g_{k}$ und $g_{- k}$ sind zueinander symmetrisch bezüglich des Koordinatenursprungs.
  Die folgende Abbildung ist in der Aufgabenstellung nicht verlangt worden.
  Sie dient nur der Veranschaulichung.
  Graphen der Funktionen $g_{1}$ und $g_{- 1}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Schreibe $- g_{- k} (x)$ auf und forme den Term so um, dass die Funktion $g_{k} (- x)$ entsteht.
  Teil 2
  Denke hier an Punktsymmetrie zum Koordinatenursprung.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Analysis, Teil B, Aufgabengruppe 2

Berechne die Koordinaten des Extrempunkts von G

Hast du eine Frage oder Feedback?

Ermittle eine Gleichung der Geraden, die den Extrempunkt von G enthält und senkrecht zu t verläuft

Hast du eine Frage oder Feedback?

Begründe, dass die Funktion f nicht umkehrbar, die Funktion h jedoch umkehrbar ist

Gib den Definitions- und den Wertebereich der Umkehrfunktion von h an

Hast du eine Frage oder Feedback?

Begründe, dass mit dem Term 2⋅((5−ln⁡5)⋅ln⁡5−∫ln⁡55f(x)dx) der Flächeninhalt der Figur berechnet werden kann

Hast du eine Frage oder Feedback?

Berechne mit dem Term aus Aufgabe 1d den Flächeninhalt der Figur auf eine Nachkommastelle genau

Hast du eine Frage oder Feedback?

Gib den zugehörigen Wert von k sowie die Koordinaten des Tiefpunkts von Graph III an

Ordne den drei übrigen Werten von k den jeweils passenden Graphen zu

Hast du eine Frage oder Feedback?

Zeige, dass gk(−x)=−g−k(x) für alle x∈ℝ gilt

Interpretiere diese Gleichung mit Blick auf die Graphen der Funktionen gk und g−k

Hast du eine Frage oder Feedback?

Berechne die Koordinaten des Extrempunkts von $G$

Ermittle eine Gleichung der Geraden, die den Extrempunkt von $G$ enthält und senkrecht zu $t$ verläuft

Begründe, dass die Funktion $f$ nicht umkehrbar, die Funktion $h$ jedoch umkehrbar ist

Gib den Definitions- und den Wertebereich der Umkehrfunktion von $h$ an

Begründe, dass mit dem Term $2 \cdot ((5 - \ln 5) \cdot \ln 5 - \int_{\ln 5}^{5} f (x) d x)$ der Flächeninhalt der Figur berechnet werden kann

Gib den zugehörigen Wert von $k$ sowie die Koordinaten des Tiefpunkts von Graph III an

Ordne den drei übrigen Werten von $k$ den jeweils passenden Graphen zu

Zeige, dass $g_{k} (- x) = - g_{- k} (x)$ für alle $x \in ℝ$ gilt

Interpretiere diese Gleichung mit Blick auf die Graphen der Funktionen $g_{k}$ und $g_{- k}$