Rätselaufgaben zu besonderen ebenen Figuren

Rätselhaft! Hier findest du Aufgaben zu besonderen ebenen Figuren. Schaffst du sie alle?

1
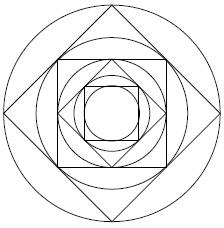
Folgende Figur besteht aus Quadraten und einbeschriebenen Kreisen.Wie ist das Verhältnis des Radius des innersten Kreises zum Radius des äußersten Kreises?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras
Inkreis und Umkreis eines Quadrates
Man bertrachtet zunächst die zwei äußersten Kreise und das äußerste Quadrat.
Der Durchmesser des Inkreises im Quadrat ist $a$ , also gilt für den Innkreisradius: $r_{i} = \frac{a}{2}$
Den Umkreisradius kann man mit Hilfe des Satz des Pythagoras berechnen:
$r_{u}^{2} + r_{u}^{2}$ $=$ $a^{2}$
$2 r_{u}^{2}$ $=$ $a^{2}$ $: 2$
$r_{u}^{2}$ $=$ $\frac{a^{2}}{2}$ $\sqrt{}$
↓
Wurzel ziehen
$r_{u}$ $=$ $\sqrt{\frac{a^{2}}{2}}$
$=$ $\frac{a}{\sqrt{2}}$
↓
Bruch erweitern
$=$ $\frac{a \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}$
$=$ $\frac{a}{{(\sqrt{2})}^{2}} \cdot \sqrt{2}$
$=$ $\frac{a}{2} \cdot \sqrt{2}$
Wir betrachten zuerst allgemein ein Quadrat mit Umkreisradius $r_{u}$ und Inkreisradius $r_{i}$ .
Löse die eben erhaltene Formel $r_{u} = \frac{a}{2} \cdot \sqrt{2}$ nach der Seitenlänge a auf:
$r_{u}$ $=$ $\frac{a}{2} \sqrt{2}$ $\cdot 2$
$2 r_{u}$ $=$ $a \sqrt{2}$ $: \sqrt{2}$
$a$ $=$ $\frac{2 r_{u}}{\sqrt{2}}$
Nun kann a in die Formel für den Inkreisradius $r_{i} = \frac{a}{2}$ eingesetzt werden:
$r_{i}$ $=$ $\frac{\frac{2 r_{u}}{\sqrt{2}}}{2}$
↓
Faktor 2 kürzen
$=$ $\frac{r_{u}}{\sqrt{2}}$
Das heißt $r_{i}$ ist $\frac{1}{\sqrt{2}} \approx 0,71$ so groß wie $r_{u}$ .
Weil diese Zusammenhang allgemein gilt, gilt er natürlich auch für das äußerste Quadrat. Also:
$r_{i 1} = \frac{r_{u 1}}{\sqrt{2}}$
Nun betrachten wir das zweite Quadrat. Der Umkreis dieses Quadrats ist der Inkreis des äußersten Quadrats. Also gilt:
$r_{i 1} = r_{u 2}$
Mit dem allgemeinen Zusammenhang zwischen In- und Umkreisradius erhalten wir:
$r_{i 2} = \frac{r_{u 2}}{\sqrt{2}} = \frac{r_{i 1}}{\sqrt{2}}$
Setze jetzt $r_{i 1} = \frac{r_{u 1}}{\sqrt{2}}$ ein und vereinfache:
$\begin{aligned} r_{i 2} & = \frac{\frac{r_{u 1}}{\sqrt{2}}}{\sqrt{2}} \\ = \frac{r_{u 1}}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} \\ = \frac{r_{u 1}}{2} \end{aligned}$
Der Umkreis des dritten Quadrats ist der Inkreis des zweiten Quadrats. Also gilt:
$r_{u 3} = r_{i 2} = \frac{r_{u 1}}{2}$
Aber auch der allgemeine Zusammenhang zwischen In- und Umkreisradius glit in diesem Quadrat:
$r_{i 3} = \frac{r_{u 3}}{\sqrt{2}}$
Setze $r_{u 3} = \frac{r_{u 1}}{2}$ ein und vereinfache:
$\begin{aligned} r_{i 3} & = \frac{\frac{r_{u 1}}{2}}{\sqrt{2}} \\ = \frac{r_{u 1}}{2} \cdot \frac{1}{\sqrt{2}} \\ = \frac{r_{u 1}}{2 \sqrt{2}} \end{aligned}$
Auch beim vierten Quadrat ist der Umkreis der Inkreis des dritten Quadrats. Damit ergibt sich:
$r_{u 4} = r_{i 3} = \frac{r_{u 1}}{2 \sqrt{2}}$
Mit dem allgemeinen Zusammenhang zwischen In- und Umkreisradius folgt:
$r_{i 4} = \frac{r_{u 4}}{\sqrt{2}}$
Setze $r_{u 4} = \frac{r_{u 1}}{2 \sqrt{2}}$ ein und vereinfache:
$\begin{aligned} r_{i 4} & = \frac{\frac{r_{u 1}}{2 \sqrt{2}}}{\sqrt{2}} \\ = \frac{r_{u 1}}{2 \sqrt{2}} \cdot \frac{1}{\sqrt{2}} \\ = \frac{r_{u 1}}{2 \cdot \sqrt{2} \cdot \sqrt{2}} \\ = \frac{r_{u 1}}{4} \end{aligned}$
Das Verhältnis des Radius des innersten Kreises zum Radius des äußersten Kreis beträgt also 1:4.
2
Während der Übertragung der US-Tennismeisterschaften 2003 in New York war im Fernsehen ein Firmenlogo zu sehen, das so ähnlich aussah wie die Abbildung unten. Der Halbkreis mit dem Mittelpunkt A und das Dreieck im Inneren des weißen Quadrates wurden zusätzlich eingezeichnet. Eine Seite des mittleren Quadrates ist $3 c m$ lang.
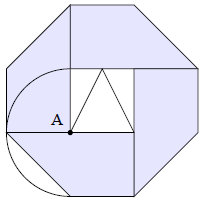
1. Begründe: Wenn der Flächeninhalt dieses Dreiecks $4,5 {cm}^{2}$ beträgt, muss eine Seite des mittleren Quadrates $3 c m$ lang sein.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
  Weil das Dreieck halb so groß wie das Quadrat ist, beträgt der Flächeninhalt des Quadrates $9 {c m}^{2}$ . Das hängt nicht davon ab, ob die Spitze dieses Dreiecks genau in der Mitte der oberen Quadratseite liegt. Eine Quadratseite ist demnach $3 c m$ lang.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Welchen Bruchteil der Gesamtfläche nimmt das Dreieck im Zentrum ein?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
  Das Logo setzt sich aus $5$ ganzen und vier halben Quadraten zusammen, deren Flächeninhalt insgesamt $63 {cm}^{2}$ beträgt.
  Anteil des mittleren Dreiecks an der Gesamtfläche: $\frac{4,5 {cm}^{2}}{63 {cm}^{2}} = \frac{1}{14}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Schneide von einem Quadrat aus Papier mit der Seitenlänge $9 c m$ die vier Ecken so ab, dass der Umriss dieses Logos entsteht.
  Wie viel Prozent des ursprünglichen Papierquadrates ist weggefallen?
  Begründe mithilfe des ursprünglichen Papierquadrates, dass das Quadrat im Inneren einen Umfang von $12 c m$ hat.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
  Es sind vier gleichschenklig-rechtwinklige Dreiecke mit einer Katheten-Länge von je $3 c m$ abgeschnitten worden.
  Abfall: $\frac{18 {cm}^{2}}{81 {cm}^{2}} = \frac{2}{9} \approx 22,22 %$ .
  Pro Seite des ursprünglichen Quadrats wurden $2 \cdot 3 c m$ weggeschnitten. $9 cm - 2 \cdot 3 c m = 3 c m$ bleiben als Seitenlänge des kleinen Quadrates übrig. Sein Umfang beträgt damit $12 c m$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
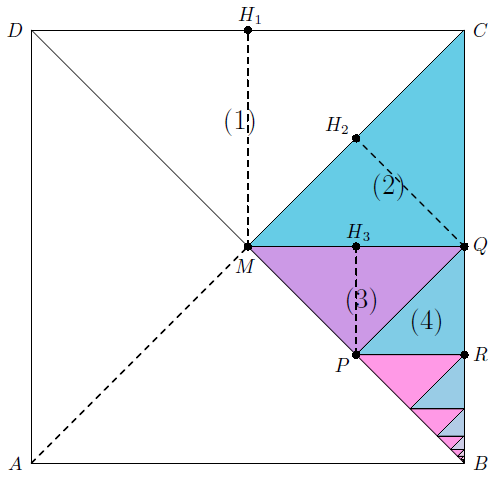
Im Quadrat $A B C D$ sind die Dreiecke $(1), (2), (3), (4), . . .$ zu sehen. Achte bei den folgenden Fragen auf die gestrichelten Hilfslinien.
1. Welche gemeinsame Besonderheiten besitzen alle diese Dreiecke?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenformeln ebener Figuren
  Alle diese Dreiecke sind gleichschenklig-rechtwinklig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Welchen Bruchteil der Quadratfläche $A_{Q}$ nimmt das Dreieck $(1)$ ein?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenformeln ebener Figuren
  $A_{(1)} = \frac{1}{4} A_{Q}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Welcher Zusammenhang besteht zwischen dem Flächeninhalt $A_{(1)}$ des Dreiecks $(1)$ und dem Flächeninhalt $A_{(2)}$ des Dreiecks $(2)$ ?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenformeln ebener Figuren
  $A_{(1)} = \frac{1}{2} A_{(2)}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Welchen Bruchteil der Quadratfläche $A_{Q}$ nehmen die beiden Dreiecke $(1)$ und $(2$ $)$ zusammen ein? Wie viel Prozent sind das?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenformeln ebener Figuren
  $\frac{1}{4} + \frac{1}{8} = \frac{3}{8} = 0,375 = 37,5 %$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Welchen Bruchteil der Quadratfläche nimmt das Dreieck $(4)$ ein?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenformeln ebener Figuren
  $A_{(4)} = A_{(3)} : 2 = A_{(2)} : 4 = A_{(1)} : 8 = \frac{1}{4} A_{Q} : 8 = \frac{1}{32} A_{Q}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. Welchen Bruchteil der Quadratfläche nehmen alle Dreiecke $(1), (2), (3), (4), . . .$ zusammen ein?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenformeln ebener Figuren
  Aus der Zeichnung erkennst du: Alle Dreiecke von $(1), (2)$ angefangen bis ins unendlich kleinste ergeben die Hälfte des Quadrates $A B C D$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. Was ergibt $\frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} \dots$ ?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenformeln ebener Figuren
  $\frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} = \frac{1}{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
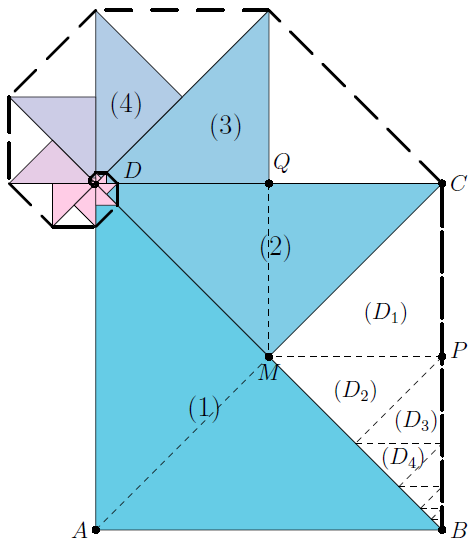
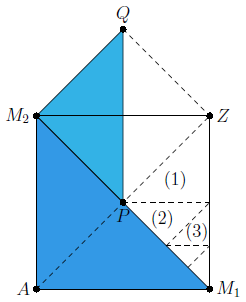
Im Quadrat $A B C D$ sind die getönten Dreiecke $(1), (2), (3), (4)$ , . . . und die ”weißen“ Dreiecke $(D 1)$ , $(D 2), (D 3), (D 4), . . .$ zu sehen.
1. Welche gemeinsame Besonderheiten besitzen alle diese Dreiecke?
  
  Alle diese Dreiecke sind gleichschenklig-rechtwinklig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Welchen Bruchteil der Quadratfläche nimmt das getönte Dreieck $(1)$ ein?
  
  $A_{(1)} = \frac{1}{2} A_{Q}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Welcher Zusammenhang besteht zwischen dem Flächeninhalt $A_{(1)}$ des Dreiecks (1) und dem Flächeninhalt $A_{(2)}$ des Dreiecks $(2)$ ? Begründe.
  
  $A_{(2)} = \frac{1}{2} A_{(1)}$
  Begründung:
  Die Diagonalen [ $A C$ ] und [ $B D$ ] zerlegen das Quadrat $A B C D$ in vier kongruente Teildreiecke, wovon eines das Teildreieck $(2)$ ist. Das Dreieck $A B D$ ist aus zwei dieser Teildreiecke zusammengesetzt. Also ist das Dreieck $(2)$ halb so groß wie das Teildreieck $(1)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Welchen Bruchteil der Quadratfläche $A Q$ nehmen die beiden getönten Dreiecke $(1)$ und $(2)$ zusammen ein? Wie viel Prozent sind das?
  
  $\frac{1}{2} + \frac{1}{4} = \frac{3}{4} = 0,75 = 75 %$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Welcher Zusammenhang besteht zwischen dem Flächeninhalt eines dieser immer kleiner werdenden getönten Dreiecke $(1), (2), (3), (4), \dots$ und seinem jeweiligen Vorgänger? Begründe deine Antwort anhand der Dreiecke $(D 1), (D 2), (D 3), (D 4) \dots$ .
  
  Es wurde schon gezeigt, dass $A_{(2)} = \frac{1}{2} A_{(1)}$ gilt.
  Die Dreiecke $M P C$ (= Dreieck $(D 1)$ ), $M C Q$ und Dreieck $(3)$ sind kongruent.
  Also gilt $A_{(3)} = \frac{1}{2} A_{(2)}$ .
  Am oben liegenden Quadrat mit der Seitenlänge [ $D Q$ ] erkennst du: $A_{(4)} = \frac{1}{2} A_{(3)}$ und die Dreiecke $(4)$ und $(D 2)$ sind kongruent.
  Insgesamt gilt: Jedes getönte Dreieck ist halb so groß wie sein Vorgänger. Jedes getönte Dreieck hat einen kongruenten Partner unter den Dreiecken $(D 1), (D 2), (D 3), (D 4), \dots$ . Jedes der Dreiecke $(D 1), (D 2), (D 3), (D 4), \dots$ . hat einen kongruenten Partner in den getönten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. Welchen Bruchteil der Fläche des Quadrates $A B C D$ nimmt das getönte Dreieck $(4)$ ein?
  
  $A_{(4)} = A_{(3)} : 2 = A_{(2)} : 4 = A_{(1)} : 8 = \frac{1}{2} A_{Q} : 8 = \frac{1}{16} A_{Q}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. Wie groß sind alle getönten Dreiecke $(1), (2), (3), (4), . . .$ zusammen?
  
  Aus der Zeichnung erkennst du: Alle Dreiecke von $(1), (2)$ angefangen bis ins unendlich kleinste ergeben das vollständige Quadrat $A B C D$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8. Was ergibt $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \dots$ ?
  
  $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \dots = 1$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9. Was ergibt $\frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \dots$ ?
  
  Da $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \dots = 1$ muss man nur noch das hinzugefügte $\frac{1}{2}$ wieder abziehen.
  $\frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \dots$
  $= 1 - \frac{1}{2} = \frac{1}{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5
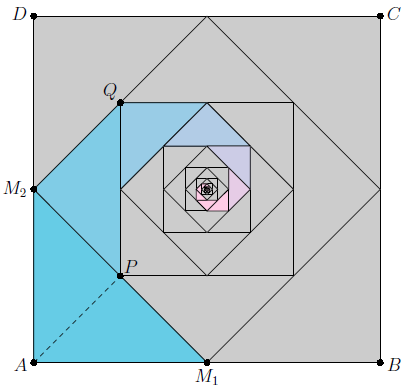
Der Schweizer Künstler Eugen Jost hat ein Bild gemalt, in dem lauter ineinander geschachtelte Quadrate dargestellt sind. Das Bild oben verdeutlicht dies.
1. Erkläre, wie Eugen Jost die Quadrate aufgebaut hat.
  
  Die Seitenmittelpunkte des großen Quadrates $A B C D$ liefern ein Quadrat, das um $90 °$ gedreht worden ist. Die Seitenmittelpunkte dieses Quadrates liefern wiederum ein kleineres Quadrat, dessen Seitenmittelpunkte erneut ein noch kleineres Quadrat erzeugen usw. Das Ganze "verschwindet" schließlich im Zentrum der Figur.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Eine chinesische Spruchweisheit lautet: "Das Unendliche ist ein Quadrat ohne Ecken." Erkläre den Zusammenhang zwischen dieser Aussage und dem Bild.
  
  Die Eckpunkte der immer kleiner werdenden Quadrate rücken näher und näher zusammen, bis sie sich nicht mehr voneinander unterscheiden lassen. Somit entsteht im Unendlichen ein "Quadrat ohne Ecken".
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. In der obigen Darstellung sind einige Dreiecke nochmals farbig herausgehoben, die sich im Uhrzeigersinn spiralförmig in das Zentrum Z des Quadrates hineinwinden. Die Spirale beginnt mit dem Dreieck ${AM}_{1} M_{2}$ .
  Welche gemeinsame Besonderheiten weisen diese Dreiecke in der Spirale auf?
  
  Diese Dreiecke sind alle gleichschenklig-rechtwinklig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Welchen Bruchteil des Flächeninhaltes des Quadrates $A B C D$ nimmt das Dreieck ${AM}_{1} M_{2}$ ein? Wie viel Prozent sind das?
  
  Das Dreieck ${AM}_{1} M_{2}$ nimmt $\frac{1}{8}$ des Flächeninhaltes des Quadrates $A B C D$ ein.
  $\frac{1}{8} = 0,125 = 12,5 %$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Begründe: Der Flächeninhalt des Dreiecks ${PQM}_{2}$ ist halb so groß wie der des Dreiecks ${AM}_{1} M_{2}$ . Betrachte dazu die gestrichelte Hilfslinie [ $A P$ ].
  
  Das Viereck ${APQM}_{2}$ ist ein Parallelogramm. Die Diagonale $[{PM}_{2}]$ zerlegt dieses Parallelogramm in zwei kongruente gleichschenklig-rechtwinklige Dreiecke. Die Strecke [ $A P$ ] zerlegt das Dreieck ${AM}_{1} M_{2}$ ebenfalls in zwei kongruente gleichschenklig-rechtwinklige Dreiecke.
  Also gilt: $A_{{ΔPQM}_{2}} = \frac{1}{2} A_{{ΔAM}_{1} M_{2}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. Zeichne das Quadrat ${AM}_{1} {ZM}_{2}$ mit einer Seitenlänge von $4 c m$ . Übertrage das Dreieck ${PQM}_{2}$ in der richtigen Position. Begründe: Alle Dreiecke in der Spirale des Bildes lassen sich lückenlos in dem Quadrat ${AM}_{1} {ZM}_{2}$ unterbringen.
  
  Das Viereck ${PZQM}_{2}$ ist ein Quadrat. Das Dreieck ${PQM}_{2}$ lässt sich also mit dem Dreieck ${PZM}_{2}$ zur Deckung bringen. Das Dreieck, das dem Dreieck ${PQM}_{2}$ unmittelbar in der Spirale folgt, ist zum Dreieck $(1)$ kongruent. Sein Nachfolger in der Spirale deckt sich mit dem Dreieck $(2)$ , dessen Nachfolger in der Spirale deckt sich mit dem Dreieck $(3)$ usw. So wird das Dreieck ${PM}_{1} Z$ nach und nach lückenlos mit Nachfolgern in der Spirale aufgefüllt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. Begründe: Der Flächeninhalt aller Dreiecke in der Spirale ergibt zusammen ein Viertel des Flächeninhaltes des Quadrates ABCD.
  
  Mit allen Dreiecken aus der Spirale lässt sich das Quadrat ${AM}_{1} {ZM}_{2}$ lückenlos füllen. Dieses Quadrat bedeckt $\frac{1}{4}$ des Quadrates ABCD.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8. Was ergibt $\frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} \dots$ ?
  
  Da $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \dots = 1$ muss man nur noch das hinzugefügte $\frac{1}{2}$ und $\frac{1}{4}$ wieder abziehen.
  $\frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \dots$
  $= 1 - \frac{1}{2} - \frac{1}{4} = \frac{1}{4}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$r_{u}^{2} + r_{u}^{2}$	$=$	$a^{2}$
$2 r_{u}^{2}$	$=$	$a^{2}$	$: 2$
$r_{u}^{2}$	$=$	$\frac{a^{2}}{2}$	$\sqrt{}$
	↓	Wurzel ziehen
$r_{u}$	$=$	$\sqrt{\frac{a^{2}}{2}}$
	$=$	$\frac{a}{\sqrt{2}}$
	↓	Bruch erweitern
	$=$	$\frac{a \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}$
	$=$	$\frac{a}{{(\sqrt{2})}^{2}} \cdot \sqrt{2}$
	$=$	$\frac{a}{2} \cdot \sqrt{2}$

$r_{u}$	$=$	$\frac{a}{2} \sqrt{2}$	$\cdot 2$
$2 r_{u}$	$=$	$a \sqrt{2}$	$: \sqrt{2}$
$a$	$=$	$\frac{2 r_{u}}{\sqrt{2}}$

$r_{i}$	$=$	$\frac{\frac{2 r_{u}}{\sqrt{2}}}{2}$
	↓	Faktor 2 kürzen
	$=$	$\frac{r_{u}}{\sqrt{2}}$

Rätselaufgaben zu besonderen ebenen Figuren

Inkreis und Umkreis eines Quadrates

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?