Aufgaben zu Polarkoordinaten
1
Bestimme die Polarkoordinaten der folgenden Punkte!
a
Der Punkt P ist 7 LE vom Koordinatenursprung entfernt und schließt mit der positiven x-Achse einen Winkel von 123° ein.
b
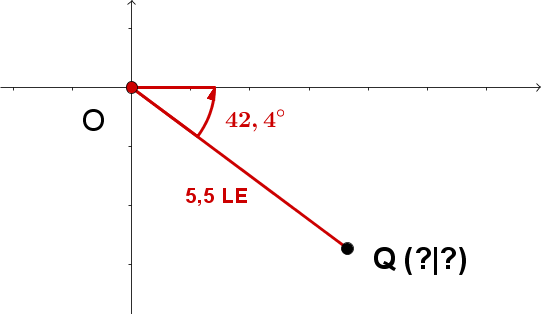
2
Rechne die Koordinaten der folgenden Punkte in Polarkoordinaten bzw. kartesische Koordinaten um!
a
b
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0. → Was bedeutet das?
Kommentare werden geladen…
