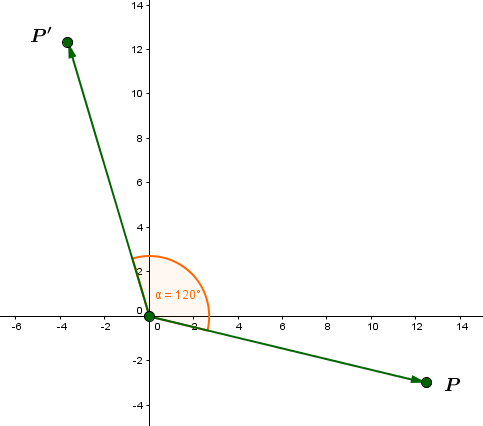
Bestimme die Abbildungsgleichung bei einer Drehung des Punktes um den Winkel um den Ursprung und die Koordinaten des dadurch abgebildeten Punktes .
Lösungsweg 1: Koordinatenform
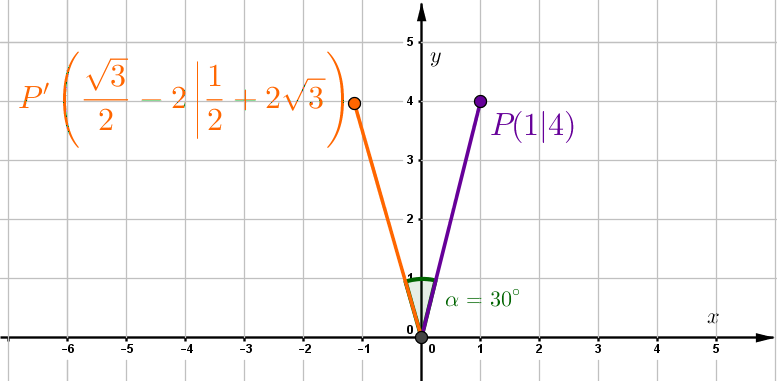
Um den Punkt um den Ursprung zu drehen, kannst du die Koordinatenform benutzen:
Um die Abbildungsgleichung zu erhalten, setzt du ein.
Um nun die Koordinaten des gedrehten Punktes zu bestimmen, setzt man die Koordinaten des ursprünglichen Punktes in die Abbildungsgleichung ein.
Dies kannst du noch weiter vereinfachen.
Nun hast du die Koordinaten des gedrehten Punktes bestimmt.
Lösungsweg 2: Matrixform
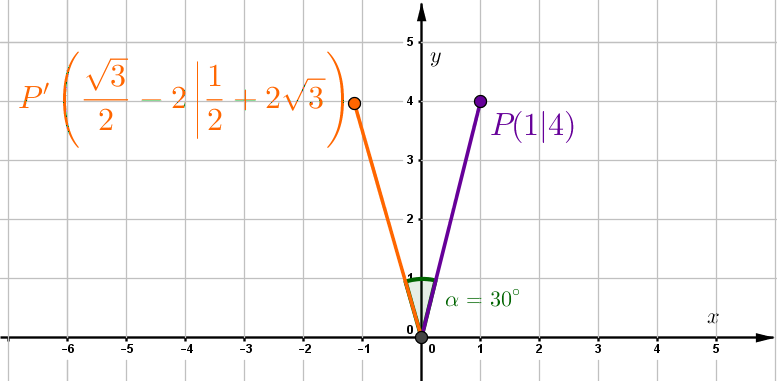
Um den Punkt um den Ursprung zu drehen, kannst du die Matrixform benutzen:
Um die Abbildungsgleichung zu erhalten, setzt du ein.
Um nun die Koordinaten des gedrehten Punktes zu bestimmen, setzt man die Koordinaten des ursprünglichen Punktes in die Abbildungsgleichung ein.
Dies kannst du noch weiter vereinfachen.
Nun hast du die Koordinaten des gedrehten Punktes bestimmt.
Hast du eine Frage oder Feedback?
Lösungsweg 1: Koordinatenform
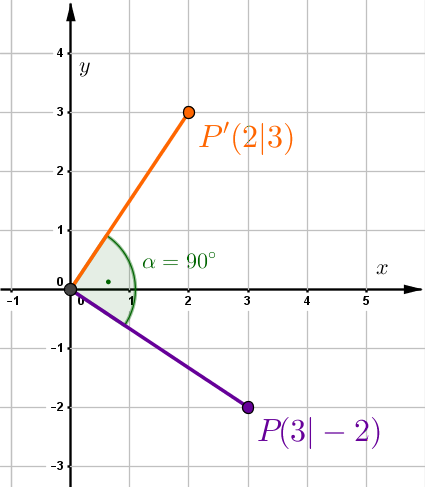
Um den Punkt um den Ursprung zu drehen, kannst du die Koordinatenform benutzen:
Um die Abbildungsgleichung zu erhalten, setzt du ein.
Um nun die Koordinaten des gedrehten Punktes zu bestimmen, setzt man die Koordinaten des ursprünglichen Punktes in die Abbildungsgleichung ein.
Dies kannst du noch vereinfachen.
Nun hast du die Koordinaten des gedrehten Punktes bestimmt.
Lösungsweg 2: Matrixform

Um den Punkt um den Ursprung zu drehen, kannst du die Matrixform benutzen:
Um die Abbildungsgleichung zu erhalten, setzt du ein.
Um nun die Koordinaten des gedrehten Punktes zu bestimmen, setzt man die Koordinaten des ursprünglichen Punktes in die Abbildungsgleichung ein.
Dies kannst du noch weiter vereinfachen.
Nun hast du die Koordinaten des gedrehten Punktes bestimmt.
Hast du eine Frage oder Feedback?
Lösungsweg 1: Koordinatenform
Skizze:
Um den Punkt um den Ursprung zu drehen, kannst du die Koordinatenform benutzen:
Um die Abbildungsgleichung zu erhalten, setzt du ein.
Um nun die Koordinaten des gedrehten Punktes zu bestimmen, setzt man die Koordinaten des ursprünglichen Punktes in die Abbildungsgleichung ein.
Dies kannst du noch vereinfachen.
Nun hast du die Koordinaten des gedrehten Punktes bestimmt.
Lösungsweg 2: Matrixform
Skizze:
Um den Punkt um den Ursprung zu drehen, kannst du die Matrixform benutzen:
Um die Abbildungsgleichung zu erhalten, setzt du ein.
Um nun die Koordinaten des gedrehten Punktes zu bestimmen, setzt man die Koordinaten des ursprünglichen Punktes in die Abbildungsgleichung ein.
Dies kannst du ebenfalls noch vereinfachen.
Nun hast du die Koordinaten des gedrehten Punktes bestimmt.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?