Aufgaben zu Fixpunkten und Fixgeraden
Hier findest du Aufgaben zur Bestimmung von Fixpunkten und Fixgeraden in Abbildungen mit Matrizen.
- 1
Prüfe durch Rechnung, ob die Gerade unter der jeweiligen Abbildung eine Fixgerade ist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung
Um den Ortsvektor eines beliebigen Punktes auf der Geraden zu finden, verschiebst du zunächst den Ortsvektor eines beliebigen Punktes auf der Geraden um den Vektor .
Jetzt kannst du erkennen, dass die untere Koordinate das dreifache der oberen beschreibt.
Daraus folgt, dass und dieselbe Gerade beschreiben.
Die beiden Geraden sind also identisch.
ist unter der Parallelverschiebung um eine Fixgerade.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung
Zunächst verschiebst du den Ortsvektor eines beliebigen Punktes auf der Geraden um den Vektor , um den Ortsvektor eines beliebigen Punktes auf der Geraden zu finden.
Nun kannst du die Steigung der Gerade berechnen und mit der Steigung der Anfangsgeraden vergleichen.
Die beiden Geraden sind also nicht identisch.
Daraus folgt, dass unter dieser Abbildung die Gerade keine Fixgerade ist.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung um den Ursprung
Du kannst die Formel für die Drehung um 180° am Ursprung für einen beliebigen Punkt auf der Geraden verwenden, um die Koordinaten eines beliebigen Punktes auf der Geraden zu finden.
Du kannst nun die Steigung des Trägergraphens , der die Koordinaten des Punktes beschreibt, bestimmen.
Sowohl hat die Steigung und geht durch den Ursprung.Damit stellst du die zugehörige Geradengleichung auf.
und haben dieselbe Geradengleichung und beschreiben daher dieselbe Gerade.
ist also eine Fixgerade
Hast du eine Frage oder Feedback?
mit
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgeraden
mit
Zunächst kannst du mit dem Arcustangens den Winkel zwischen der Geraden und der x-Achse bestimmen.
Nun kannst du den allgemeinen Punkt auf der Gerade an der Gerade spiegeln um den Pukt zu erhalten.
Nun kannst du die Steigung der gespiegelten Gerade ausrechnen.
Sowohl hat die Steigung und geht durch den Ursprung.Damit stellst du die zugehörige Geradengleichung auf.
und haben dieselbe Geradengleichung und beschreiben daher dieselbe Gerade.
ist also eine Fixgerade
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Zentrische Streckung
Die zentrische Streckung bildet Urprungsgeraden immer auf sich selbst ab.
Dies erkennt man auch rechnerisch:
Du kannst die Formel für die zentrische Streckung für einen beliebigen Punkt auf der Geraden verwenden, um die Koordinaten eines beliebigen Punktes auf der Geraden zu finden.
Der Ursprung erfüllt diese Voraussetzung, was du durch Einsetzten rausfindest.
Nun kannst du die Steigung der gestreckten Gerade ausrechnen.
Sowohl hat die Steigung .Damit stellst du die zugehörige Geradengleichung auf.
und haben dieselbe Geradengleichung und beschreiben daher dieselbe Gerade.
ist also eine Fixgerade
Hast du eine Frage oder Feedback?
mit
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgeraden
mit
Zunächst kannst du mit dem Arcustangens den Winkel zwischen der Geraden und der x-Achse bestimmen.
Nun kannst du den allgemeinen Punkt auf der Gerade an der Gerade spiegeln um den Pukt zu erhalten.
Nun kannst du die Steigung der gespiegelten Gerade ausrechnen und mit der Steigung der ursprünglichen vergleichen.
Die beiden Geraden sind also nicht identisch.
Daraus folgt, dass unter dieser Abbildung die Gerade keine Fixgerade ist.
Hast du eine Frage oder Feedback?
- 2
Welche Punkte sind unter diesen Abbildungen Fixpunkte?
mit und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgeraden
mit und
Zunächst kannst du mit dem Arcustangens den Winkel zwischen der Geraden und der x-Achse bestimmen.
Nun kannst du den allgemeinen Punkt auf der Gerade an der Gerade spiegeln um den Pukt zu erhalten.
Nun kannst du die Steigung der gespiegelten Gerade ausrechnen.
Wenn du für einsetzt stellst du fest, dass der Ursprung auf der Gerade liegt.
Damit kannst du die Geradengleichung für aufstellen.
Nun kannst du die beiden Gleichungen und gleichsetzen um die x-Koordinate des Schnittpunktes zu finden. Dieser ist auch der Fixpunkt der Spiegelung von an .
Damit kannst du nun die y-Koordinate berechnen, indem du den x-Wert in eine der beiden Gleichungen und einsetzt.
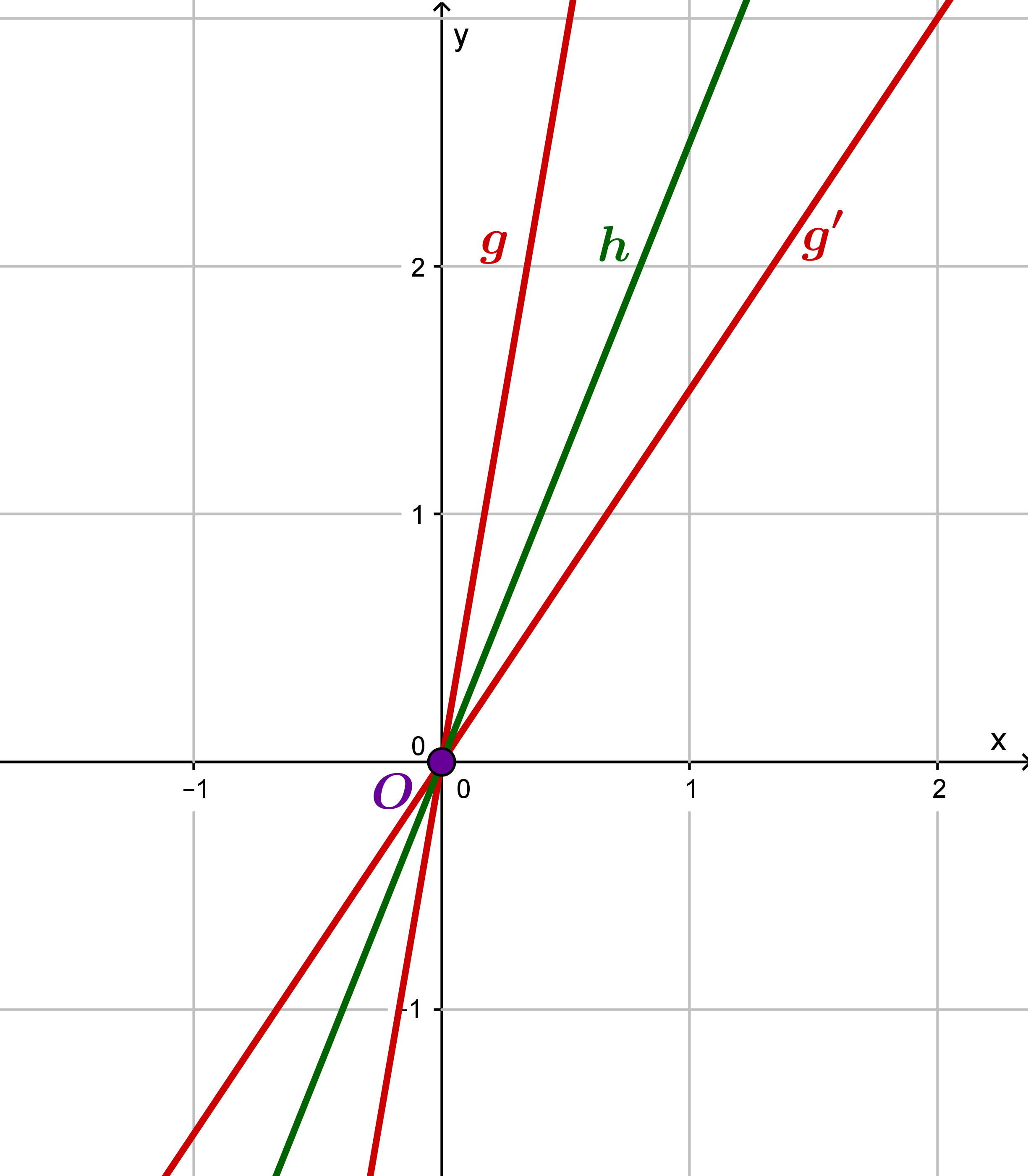
Der Fixpunkt der Abbildung ist also der Ursprung .
Hast du eine Frage oder Feedback?
mit
Für diese Aufgabe benötigst Du folgendes Grundwissen: Zentrische Streckung
Die zentrische Streckung bildet Urprungsgeraden immer auf sich selbst ab.
Dies erkennt man auch rechnerisch:
mit
Du kannst die Formel für die zentrische Streckung für einen beliebigen Punkt auf der Geraden verwenden, um die Koordinaten eines beliebigen Punktes auf der Geraden zu finden.
Der Ursprung erfüllt diese Voraussetzung, was du durch Einsetzten rausfindest.
Nun kannst du die Steigung der gestreckten Gerade ausrechnen.
Jetzt stellst du die Geradengleichung für auf.
Diese stimmt mit der Gleichung für überein. Wenn du sie nun gleichsetzt, stellst du fest, dass für alle erfüllt ist.
Alle Punkte auf werden wieder auf Punkte auf abgebildet. Die komplette Gerade ist daher eine Fixgerade.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
