1 Übersicht
Inhalt des Kurses
Ziel dieses Kurses ist es, das Erweitern und Kürzen von Brüchen kennenzulernen und für den Größenvergleich zu verwenden.
Vorkenntnisse
Du solltest wissen, was Brüche sind.
Kursdauer
Der Kurs dauert ungefähr 1,5 Stunden (Wenn du die Übungsaufgaben alle selbstständig lösen möchtest).
2 Verschiedene Brüche mit dem gleichen Wert
Aufgabe
Die Pizzabäcker Marco und Giovanni backen gleich große Pizzen. Marco teilt seine Pizza in 6 gleich große Stücke. Pizzabäcker Giovanni dagegen teilt seine Pizza in nur 4 Stücke.
Du kaufst bei Marco 3 Stück Pizza und dein Freund bei Giovanni 2 Stück Pizza. Wer von euch beiden hat mehr Pizza bekommen?
Schau genau hin und vergleiche die Stücke. Was fällt dir auf?

Richtig! Ihr habt beide gleich viel Pizza. Ist das nicht erstaunlich? Du hast Pizza gekauft und dein Freund und trotzdem habt ihr gleich viel Pizza.
Schauen wir uns dazu ein weiteres Beispiel an
Welcher Bruchteil ist rot? Schreibe als Bruch.



Ist dir aufgefallen, dass die rote Fläche immer gleich groß ist und du trotzdem unterschiedliche Brüche verwendet hast, um sie zu beschreiben?
Zusammenfassung
Um ein und denselben Bruchteil darzustellen, können wir verschiedene Brüche verwenden. Andersherum stellen manchmal verschiedenen Brüche den gleichen Bruchteil dar.
Was es damit genauer auf sich hat, lernst du in den folgenden Kapiteln.
3 Was heißt Erweitern?
Im vorigen Abschnitt hast du kennengelernt, dass zwei Brüche den gleichen Bruchteil beschreiben können. Was das bedeutet, schauen wir uns nun genauer an.
Wie sieht das anschaulich aus?
Der hier blau gefärbte Bruchteil ist .

Wenn wir jeden Teil einmal halbieren, erhalten wir .

Unterteilen wir jeden Teil noch einmal, dann sind es .

Anschaulich ist dadurch klar, dass gilt:
Was bedeutet das mathematisch?
Wenn wir bei dem Bruch den Zähler (1) und den Nenner (3) mit der Zahl 2 multiplizieren, erhalten wir den Bruch :
Genauso erhalten wir , indem wir bei den Zähler (2) und Nenner (6) jeweils mit 2 multiplizieren:
Formal können wir das schreiben als:
Dieses Vorgehen nennt man "Erweitern".
Anschaulich betrachtet bedeutet "Erweitern" eine Verfeinerung der Unterteilung,
mathematisch die Multiplikation von Zähler und Nenner mit der gleichen Zahl.
Wichtig: Der Wert des Bruchs ändert sich dabei nicht!
Beispiel
Erweitere den Bruch mit 3.
Anschaulich:
Teile alle 5 Teile in jeweils 3 gleich große Teile.

Mathematisch:
Multipliziere Zähler und Nenner mit der Zahl 3.
oder
Übungsaufgaben
1) Erweitere mit 2.
2) Erweitere mit 5.
3) Erweitere die drei Brüche so, dass sie alle den Nenner 40 haben.
4) mit welcher Zahl wurde hier erweitert?
4 Was heißt Kürzen?
Im vorigen Kapitel hast du gelernt, dass sich Brüche erweitern lassen, indem man die Bruchteile in gleich große Teilstücke unterteilt bzw. Zähler und Nenner mit der gleichen Zahl multipliziert.
Wir können aber umgekehrt Teilstücke zusammenfassen bzw. Zähler und Nenner durch die gleiche Zahl dividieren.
Beispiel
des Rechtecks sind blau gefärbt.

Wenn wir jeweils zwei nebeneinanderliegende Felder zusammenfassen, lässt sich der blau gefärbte Bruchteil des Rechtecks schreiben als schreiben.

Fassen wir nochmals jeweils 2 übereinander Felder zusammen, erhalten wir den Bruch .

Anschaulich ist dadurch auch klar, dass gilt:
Anstatt wie beim Erweitern Zähler und Nenner mit der gleichen Zahl zu multiplizieren, können wir also auch Zähler und Nenner durch die gleiche Zahl dividieren.
Hier gilt: und
Formal können wir das schreiben als:
Dieses Vorgehen nennt man "Kürzen".
Mathematisch die Division von Zähler und Nenner mit der gleichen Zahl.
Beispiele
Kürze den Bruch mit der Zahl 3.
Anschaulich:
Fasse jeweils 3 Teile zusammen
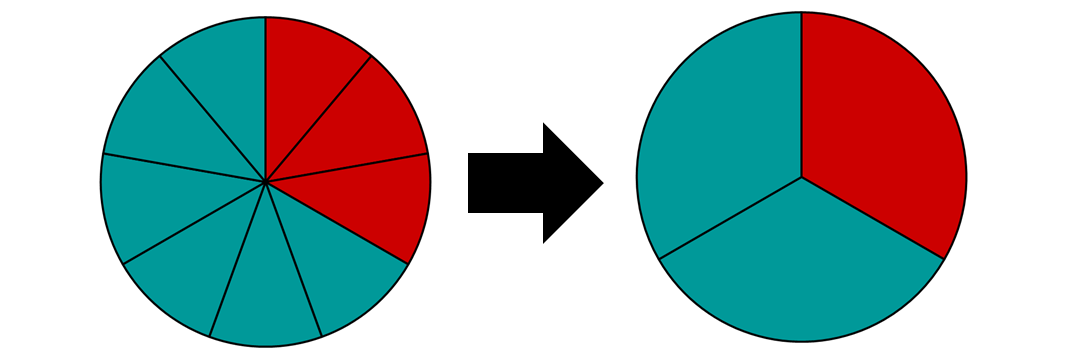
Mathematisch:
Dividiere Zähler und Nenner durch die Zahl 3
oder
Übungsaufgaben
1)
Laden
2)
Laden
3)
Laden
5 Wie kann man die Größe von Brüchen vergleichen? I
Wir haben in den vorherigen Kapiteln festgestellt, dass wir Brüche auf dem Zahlenstrahl einzeichnen können. Brüche beschreiben also immer einen Zahlenwert. Wir wollen uns nun anschauen, wie wir diesen Zahlenwert verschiedener Brüche vergleichen können. Schauen wir uns dazu den Bruchteil der roten Teile der beiden folgenden Kreise an:
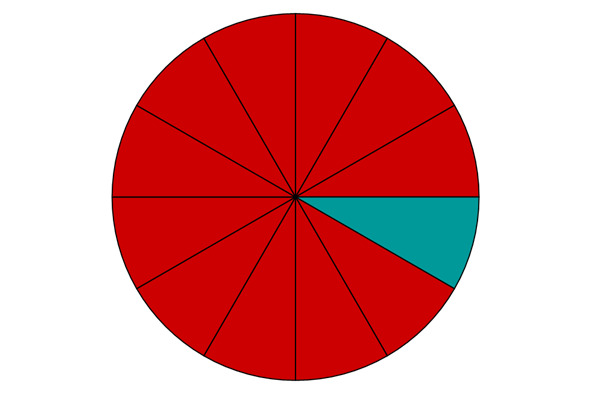
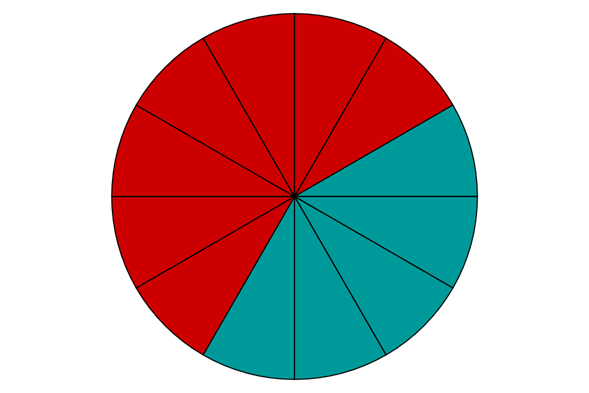
Der erste Kreis beschreibt den Bruchteil , der zweite . Der erste Bruch ist größer, da man ja mehr Teile (oder Stücke einer Pizza) hat. Es gilt also: .
Merke: Vergleicht man zwei Brüche mit gleichem Nenner, dann ist der Bruch mit dem größeren Zähler größer.
Was passiert aber jetzt, wenn die Nenner nicht gleich sind? Betrachten wir dazu den Bruchteil der roten Teile der folgenden Kreise:
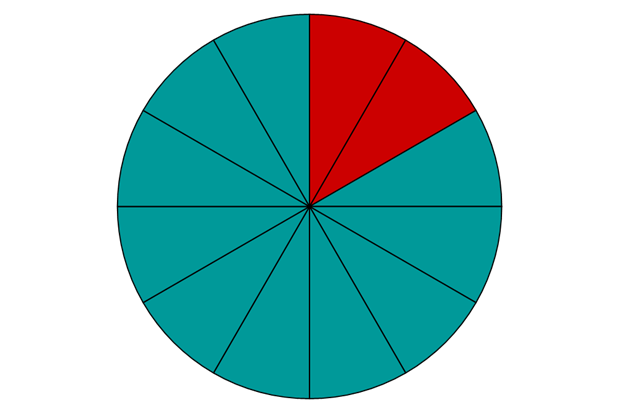
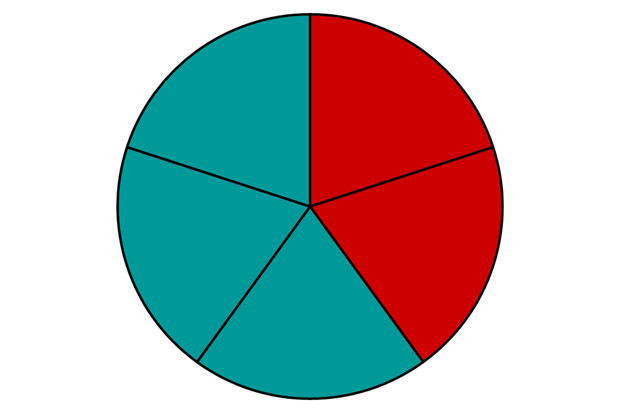
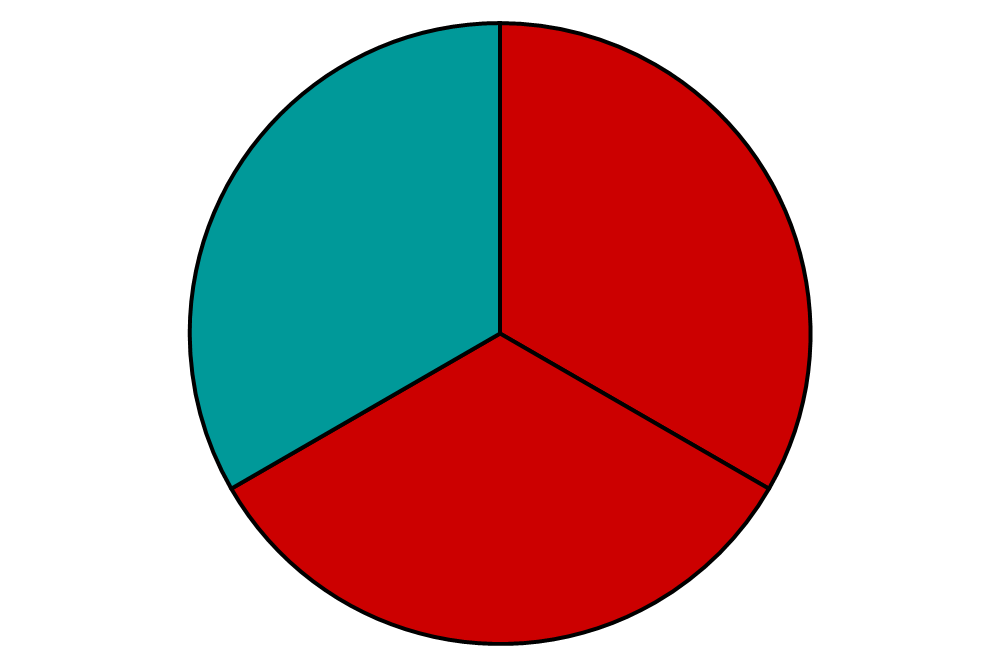
Diesmal vergleichen wir also die Brüche , und . Der dritte Bruch ist der größte, da die beiden Teile größer sind: . In je mehr Stücke wir eine Pizza unterteilen, desto kleiner werden die Stücke.
Merke: Vergleicht man zwei Brüche mit gleichem Zähler, dann ist der Bruch mit kleinerem Nenner größer.
Wir haben in diesem Kapitel gelernt, wie man Brüche vergleicht, deren Nenner oder Zähler gleich sind. Im nächsten Kapitel werden wir uns anschauen, was passiert, wenn weder Zähler noch Nenner gleich sind.
Welcher der beiden Brüche ist größer?
oder ?
oder ?
oder ?
oder ?
6 Wie kann man die Größen von Brüchen vergleichen? II
Wie können wir die Brüche , und vergleichen? Unsere Merkregeln aus dem vorherigen Abschnitt helfen hier nicht weiter: Weder stimmen die Zähler noch die Nenner überein. Wir können jedoch die Nenner durch Erweitern und Kürzen anpassen. Können wir dabei die Brüche so erweitern, dass sie zum Schluss alle denselben Nenner haben? Wir haben in einer vorherigen Übungsaufgabe gesehen, dass wir in diesem Fall alle Brüche auf den gemeinsamen Nenner 40 erweitern können:
Nach unserer Merkregel für Brüche mit selbem Nenner folgt also: oder .
Dieses Vorgehen können wir auf irgendwelche Brüche anwenden: Wollen wir Brüche vergleichen, die weder den gleichen Zähler noch Nenner haben, so müssen wir diese Brüche auf einen gemeinsamen Nenner, genannt Hauptnenner, erweitern. Dazu bestimmt man das kleinste gemeinsame Vielfache (kgV) der auftretenden Nenner und erweitert alle Brüche auf dieses Vielfache. Im obigen Beispiel war dies 40, und wir haben die Brüche mit 5, 8 bzw. 10 erweitert.
Merke: Brüche kann man nur dann vergleichen, wenn entweder die Zähler oder Nenner gleich sind.
Falls die Nenner gleich sind, so ist der Bruch mit dem größeren Zähler größer.
Falls die Zähler gleich sind, so ist der Bruch mit dem kleineren Nenner größer.
Stimmen weder Zähler noch Nenner überein, so bringt man die Brüche auf einen gemeinsamen Nenner, meistens durch Erweitern.
Welche der beiden Brüche ist größer?
oder ?
oder ?
oder ?
7 Übungsaufgaben
Gemischte Zahlen
Rechne die gemischte Zahl in einen Bruch um
Wandle den Bruch in eine gemischte Zahl um
Erweitern und Kürzen
Mit welcher Zahl wurde erweitert?
Erweitere mit der Zahl 4
Erweitere schrittweise
Mit welcher Zahl wurde gekürzt?
Suche die Kürzungszahl und bestimme den fehlenden Wert
Größenvergleich von Brüchen
Ordne die folgenden Brüche der Größe nach (fange mit dem kleinsten Bruch an)
Welche der beiden Brüche ist größer?
oder ?
oder ?
oder ?
oder ?
