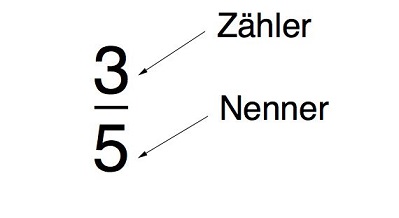
Arten von Brüchen
Man unterscheidet
echte Brüche (Betrag des Zählers ist kleiner als Betrag des Nenner)
unechte Brüche (Betrag des Zählers ist größer oder gleich Betrag des Nenners)
gemischte Brüche (ganze Zahl + Bruch)
Scheinbruch (Bruch hat als Wert eine ganze Zahl). .
Außerdem gibt es noch die Begriffe
Stammbruch (Zähler ist 1)
Doppelbruch (im Zähler und / oder im Nenner steht selbst wieder ein Bruch).
Rechnen mit Brüchen
Eine Zusammenfassung der Regeln, wie man mit Brüchen rechnet, findet man im Artikel
Genaueres findet man jeweils in folgenden Artikeln:
zum Kürzen und Erweitern: Brüche kürzen und erweitern,
zum Plus- und Minus-Rechnen: Brüche addieren und subtrahieren,
zum Mal- und Geteilt-durch-Rechnen: Brüche multiplizieren und dividieren.
Bedeutung eines Bruches
Einen Bruch kann man in verschiedener Hinsicht verstehen:
Man kann damit die Größe eines Anteils an einem Ganzen ausdrücken.
Man kann einen Bruch als andere Schreibweise für eine Geteilt-durch-Rechnung oder Division verstehen.
Man kann mit einem Bruch das Verhältnis zweier ganzer Zahlen zueinander ausdrücken.
1. Bruch zur Angabe der Größe eines Anteils
Mit Brüchen kann man ausdrücken, dass von etwas nicht ein Ganzes, sondern nur ein Teil eines Ganzen gemeint ist, und dazu sagen, wie groß dieser Teil sein soll.
Beispiel:
Der Bruch
"drei Viertel"
Der Kreis wurde in 4 Teile unterteilt; jedes Teil ist ein Viertel des Kreises.
Wenn 3 der 4 Teile ausgewählt werden, sind das drei Viertel des Kreises.

Im Nenner steht, in wie viele Teilstücke insgesamt das Ganze unterteilt wurde. Im Zähler steht, wie viele Teilstücke ausgewählt sind.
Der Nenner des Bruches "benennt" die Art der Anteile.
Der Zähler "zählt", wie viele ausgewählt sind.
2. Bruch als "Geteilt-durch"-Rechnung
Die Bruchschreibweise ist eine andere Schreibweise für die Division, wobei der Zähler der Dividend und der Nenner der Divisor ist.
Beispiel:
Jeder Bruch kann als Divisionsaufgabe und jede Divisionsaufgabe kann als Bruch geschrieben werden.
Daraus folgt, dass jede ganze Zahl als Bruch geschrieben werden kann, da ja zum Beispiel ist.
3. Bruch als Verhältnis zweier Zahlen zueinander
Brüche sind eine Möglichkeit, Verhältnisse anzugeben. Dabei stehen sowohl im Zähler als auch im Nenner ganze Zahlen.
Beispiel: " der Äpfel sind grün" kann sowohl " von Äpfeln sind grün" als auch " von Äpfeln sind grün" bedeuten. Die Menge der Äpfel unterscheidet sich, aber das Verhältnis bleibt gleich. Die Vorstellung als Verhältnis kann später beim Erweitern von Brüchen hilfreich sein.
Null im Nenner
Aber warum nicht?
Gegeben:
Als Ergebnis würden wir eine erhalten, da
Im Umkehrschluss gilt dann logischerweise auch
Gegeben:
Angenommen, die Lösung von wäre eine Zahl . Dann würde wie oben gelten: .
Da aber jede Multiplikation mit wieder ergibt, ist die Gleichung falsch und für keine Zahl lösbar.
Es gibt deshalb auch keine Lösung für - der Bruch ist nicht definiert.
Weil der Umkehrschluss nicht gilt, ist auch die Division durch null nicht erlaubt!
Andere Begründung, warum Nenner nicht Null werden darf
Aus der Grundschule kennt man die Vorstellung der Division als Aufteilen oder Verteilen. Die Aufgabe kann man also auffassen als " Bonbons werden gerecht an Kinder verteilt. Wie viele Bonbons bekommt ein Kind?"
Bei einer Aufgabe wie bzw. müssten die Bonbons also an Kinder verteilt werden. Da Bonbons aber nicht einfach so verschwinden, man sie also nicht an niemanden verteilen kann, macht diese Aufgabe keinen Sinn.
Anschauliche Darstellungen
Kreisdarstellung
Im ersten Schritt stellt man sich einen ausgefüllten Kreis vor.
Diesen betrachtet man als 1, für 1 Ganzes.

Diesen Kreis unterteilt man nun in 8 gleich große Teile.
Eines dieser "Kuchenstücke" hat jetzt in Bezug auf den ganzen Kreis noch die Größe .
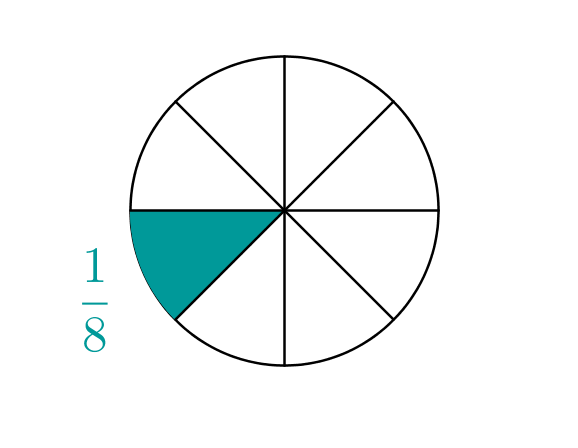
Zählt man nun 3 dieser Kuchenstücke zusammen, so hat man:
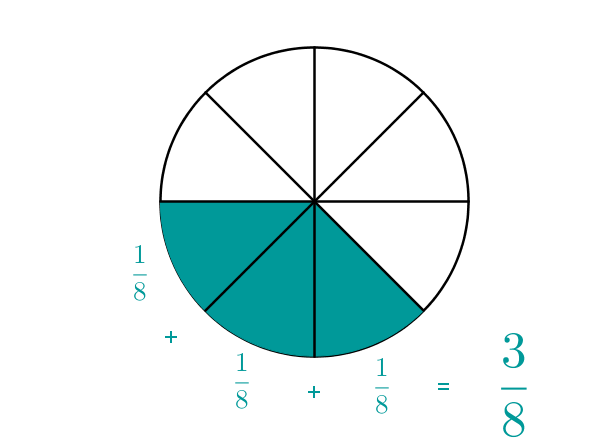
Darstellung am Zahlenstrahl
Will man Brüche am Zahlenstrahl darstellen, so muss man die Intervalle zwischen den ganzen Zahlen geeignet teilen.
Für den Bruch benötigt man zum Beispiel 8 Abschnitte. Der Bruch wird dann, weil der Zähler 3 ist, bei dem Strich nach dem dritten Abschnitt eingetragen. Weitere Beispiele findet man im Artikel Zahlengerade.

Video zum Thema Bruch
Laden
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur graphischen Veranschaulichung von Bruchteilen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema: