Aufgaben zu Exponentialfunktionen

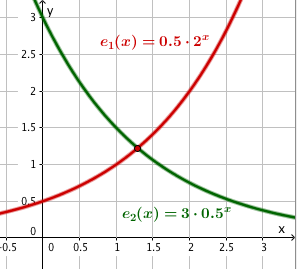
Graphisches Lösen von Exponentialgleichungen

Einführungsbeispiel

Löse die Gleichung $x^2=2^x$ graphisch.

Lösung

$\underbrace{x^2}_{f(x)}=\underbrace{2^x}_{e(x)}$

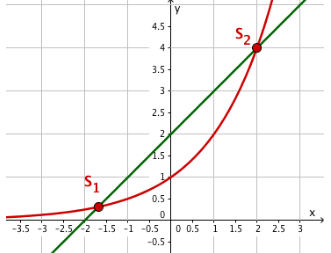
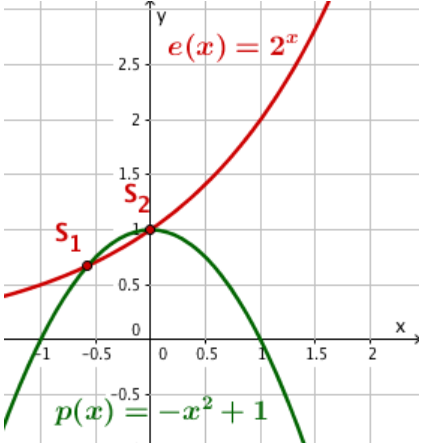
Zeichne den Graphen der Parabel $f(x)=x^2$ und den der Exponentialfunktion $e(x)=2^x$ .

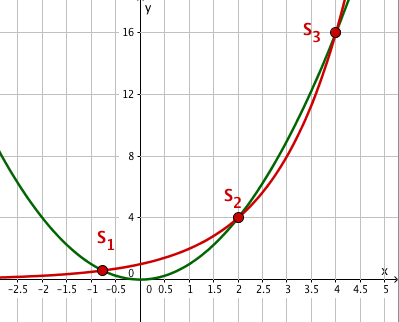
Die x-Koordinaten der gemeinsamen Punkte (Schnittpunkte) beider Graphen sind die gesuchten Lösungen der Gleichung $x^2=2^x$ .

\displaystyle \def\arraystretch{1.25} \begin{array}{l}x_1\approx-0{,}8\\x_2=2\\x_3=4\end{array}

Die ganzzahligen Lösungen $x_2=2$ und $x_3=4$ findet man natürlich auch durch Probieren. $x_1$ (eine irrationale Zahl) als Näherungswert nur graphisch.

Oft will man nur feststellen, ob eine Gleichung überhaupt lösbar ist, oder es reichen grobe Näherungswerte der Lösungen, dann genügen für die graphische Lösung Handskizzen der Graphen. Willst du es genauer, dann verwendest du einen Funktionsplotter zum Zeichen der Graphen.

Für die anschließenden Aufgaben sollen Handskizzen genügen.

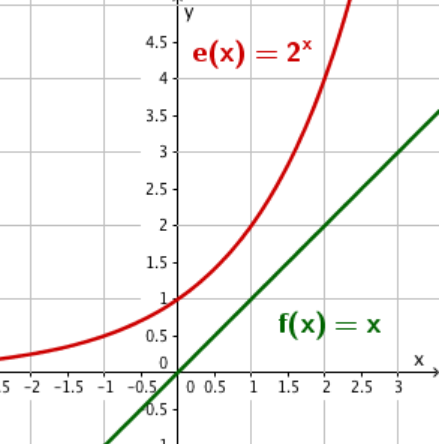
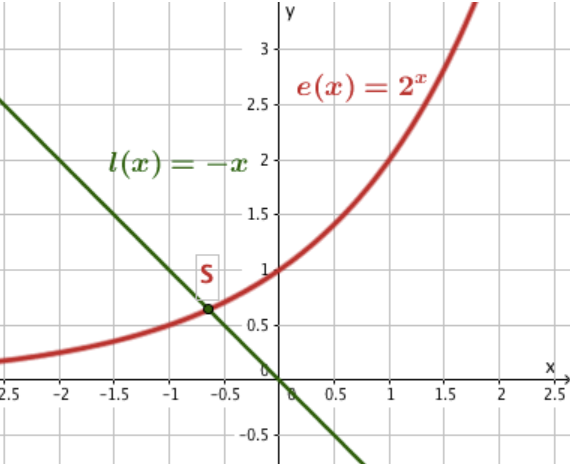
Löse die Exponentialgleichung $x+2=2^x$ graphisch.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
Schneide den Graphen der Exponentialfunktion $x\mapsto2^x$ mit dem Graphen der linearen Funktion $x\mapsto x+2$ und löse damit graphisch die Gleichung $x+2=2^x$ .
$\quad\quad\quad$
Ablesen der $x$ -Koordinaten der Schnittpunkte der Graphen ergibt:
Also gilt: $\mathbb{L}=$ { $-1{,}7;2$ }
Den exakten zweiten Wert kannst du leicht du Einsetzen in die Gleichung bestätigen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Löse die Exponentialgleichung $\def\arraystretch{1.25} \begin{array}{l}x=2^x\end{array}$ graphisch.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
Schneide - falls möglich - den Graphen der Exponentialfunktion $e:x\mapsto 2^x$ mit der linearen Funktion $f: x \mapsto x$ und löse damit die Gleichung $x=2^x$ .
$\quad\quad\quad$
Die beiden Graphen haben keine Punkte gemeinsam. Deshalb hat die Gleichung $x=2^x$ keine Lösung.
Es ist $\mathbb{L}={\;}$ { }.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Löse die Exponentialgleichung $2^x+x\;=0$ graphisch.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
Löse die Gleichung $2^x+x=0$ graphisch.
$2^x+x=0$ $\;$ $\left|-x\right.$
Forme die Gleichung um.
$2^x=-x$
Schneide den Graphen der Exponentialfunktion $e(x)=2^x$ mit dem Graphen der linearen Funktion $l(x)=-x$ und löse damit die Gleichung $2^x+x=0$
Die Graphen schneiden sich in einem Punkt mit dem Näherungswert $x\approx -0{,}64$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Löse die Exponentialgleichung $2^x+x^2-1=0$ graphisch.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
$2^x+x^2-1=0$ $\;$ $\left|1-x^2\right.$
Stelle den Funktionsterm $2^x$ alleine auf eine Seite der Gleichung.
$2^x=-x^2+1$
Schneide den Graphen der Exponentialfunktion $e(x)=2^x$ mit der Parabel $p(x)=-x^2+1$ .
Lies die $x$ -Koordinaten der Schnittpunkte aus der Zeichnung ab.
$\def\arraystretch{1.25} \begin{array}{l}x_1\approx-0{,}57\\x_2=0\end{array}$
Mache für $x_2$ die Rechenprobe!
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Löse die Exponentialgleichung $0{,}5\cdot2^x=3\cdot0{,}5^x$ graphisch und - falls du den Logarithmus schon kennst - auch rechnerisch.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
Graphische Lösung
$0{,}5\cdot2^x=3\cdot0{,}5^x$
Schneide die Graphen der Exponentialfunktionen $e_1(x)=0{,}5\cdot2^x$ und $e_2(x)=3\cdot0{,}5^x$ .
Lies die x-Koordinate des Schnittpunktes aus deiner Skizze ab.
$x\approx1{,}30$
Rechnerische Lösung
$0{,}5\cdot2^x=3\cdot0{,}5^x$
$0{,}5\cdot2^x=3\cdot\left(\frac12\right)^x$
$0{,}5\cdot2^x=3\cdot\frac1{2^x}$
Setze $2^x=u$
$\;\;0{,}5\cdot u=\frac3u$ $\;$ $\left|\cdot u\right.$
$0{,}5\cdot u^2=3$
$u^2=6$ $\;$ $\mid\sqrt{}$
$\def\arraystretch{1.25} \begin{array}{l}u_1=+\sqrt6\\u_2=-\sqrt6\end{array}$
Nur $+\sqrt6$ kommt in Frage. Ersetze u.
$2^x=\sqrt6$
Löse nach x durch Logarithmieren auf.
$\displaystyle x=\frac{\ln(\sqrt6)}{\ln(2)}$
Jetzt ist der Taschenrechner dran.
$x\approx1{,}29$
Vergleiche das Rechenergebnis mit deinem graphischen Wert. Bist du zufrieden?
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Einführungsbeispiel

Lösung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Graphische Lösung

Rechnerische Lösung

Hast du eine Frage oder Feedback?