Aufgaben zur Oberfläche - lernen mit Serlo!

Ein Tempel soll restauriert werden, da er ziemlich verfallen ist. Im Rahmen der Sanierungsarbeiten soll er auch einen neuen Anstrich bekommen.

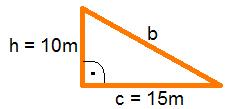
Die Maße des Tempels kannst du aus dem Bild unten entnehmen.

Zusätzlich gibt dir der Bauleiter folgende Informationen:

Die Länge des Tempels ist insgesamt $90 \;\mathrm{m}$ , die in drei gleich lange Teilstücke aufgeteilt sind.
Auf der Rückseite befinden sich $9$ Säulen, an jeder Breitseite jeweils $5$ und vorne insgesamt $10$ .
Der Boden mit der Treppenstufe muss nicht saniert werden

Berechne, für wie viel Fläche die Farbe reichen muss, wenn nur die Säulen gestrichen werden sollen.

Das Dach bekommt einen wasserfesten Anstrich. Dazu wird alles gestrichen, was vom Regen erreicht werden kann, das heißt alles außer die Unterseite des Daches.

Berechne, für wie viel Fläche die wasserfeste Farbe reichen muss.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Oberflächenformeln von Körpern

Oberfläche der Seitendächer

Die Seitendächer sind Quader, dessen Oberfläche du so berechnen kannst:

\displaystyle O_{Quader}=2\cdot l\cdot b+2\cdot l\cdot h+2\cdot b\cdot h

( $l$ : Länge des Quaders, $b$ : Breite des Quaders, $h$ : Höhe des Quaders)

Überlege dir jetzt, welche Seiten wirklich gestrichen werden müssen. Du brauchst nur eine $l\cdot b$ Seite und nur eine $l\cdot h$ Seite und zwei $b\cdot h$ Seiten.

$\displaystyle O_{Seitendach}$	$=$	$\displaystyle l\cdot b+l\cdot h+2\cdot b\cdot h$
	↓	Setze die gegebenen Werte ein: $l=90\text m :3=30\text m, h=50\text m, h=5\text m$
	$=$	$\displaystyle 30\;\mathrm{m}\cdot 50\;\mathrm{m} + 50\;\mathrm{m} \cdot 5\;\mathrm{m} + 2\cdot 30\;\mathrm{m} \cdot 5\;\mathrm{m}$
	$=$	$\displaystyle 2050\text{m}^2$

Das ganze brauchst du zwei mal, da es zwei Seitendächer gibt.

\displaystyle O_{Seitendächer}=2\cdot 2050\;\mathrm{m}^2=4100\;\mathrm{m}^2

Oberfläche Mittelteil

Zur Oberfläche vom Mittelteil gelangst du, indem du

die zwei Seiten vom Spitzdach
die Vorder und Rückseite, die sich aus Rechteck und Dreieck zusammensetzen
die zwei Seitenflächen vom Vordach

ausrechnest. $A$ bezeichnet hier immer die Fläche.

\displaystyle A_{Spitzdach\ Oberseite}=2\cdot l\cdot b

Die Seitenflächen brauchst du zweimal. Die Länge ist $60\;\mathrm{m}$ . Aber wie lang ist die Breite?

Berechnung der Breite des Seitendachs

Betrachte dazu das Dreieck, das du auf der Vorderseite siehst. Aus diesem musst du jetzt die fehlende Länge ausrechnen. Dies machst du mit dem Satz des Pythagoras.

Wie kommst du jetzt auf die fehlende Strecke?

$h^{2} + c^{2} = b^{2}$ $\Rightarrow$ $b= \sqrt{h^2+c^2}$ .

Setze die Werte ein.

$\displaystyle b$	$=$	$\displaystyle \sqrt{h^2+c^2}$
	↓	Setze $h = 10 m$ und $c= 30\text m :2 = 15 \text m$ ein.
	$=$	$\displaystyle \sqrt{\left(10\text{m}\right)^2+\left(15\text{m}\right)^2}$
	$=$	$\displaystyle \sqrt{100\text{m}^2+225\text{m}^2}$
	$=$	$\displaystyle \sqrt{325\text{m}^2}$
	↓	Zerlege $325$ in seine Primfaktoren um teilweise zu radizieren.
	$=$	$\displaystyle \sqrt{5\cdot5\cdot13}\text{m}\$
	↓	Radiziere teilweise.
	$=$	$\displaystyle 5\sqrt{13}\text{m}\$

Mit dieser Breite kannst du jetzt weiter rechnen.

Berechnung der Fläche der Oberseite des Spitzdachs

$\displaystyle A_{Spitzdach\ Oberseite}$	$=$	$\displaystyle 2\cdot l\cdot b$
	↓	Die Breite hast du gerade ausgerechnet und die Länge ist $60\;\mathrm{m}$ .
	$=$	$\displaystyle 2\cdot60\text{m}\cdot5\sqrt{13}\text{m}\$
	$\approx ≈$	$\displaystyle 2163{,}33\text{m}^2$

Berechnung der Oberfläche des Spitzdachs vorne

\displaystyle A_{Spitzdach\ Vorderseite}=A_{Dreieck}+A_{Rechteck}

Wie geht die Flächenformel für Dreiecke? Jetzt benötigst du aber wieder ein anderes Dreieck, nämlich das, was du auf der Vorderseite des Daches siehst.

$\displaystyle A_{Spitzdach\ Vorderseite}$	$=$	$\displaystyle A_{Dreieck}+A_{Rechteck}$
	↓	Die Fläche des Dreiecks bestimmst du mithilfe der Höhe $h$ und die Länge der Grundseite $g$ .
	$=$	$\displaystyle \frac{1}{2}\cdot g\cdot h+l\cdot b$
	↓	Setze die gegebenen Werte ein: $g=30\text m, h=10\text m, l=30\text m$ und $b=5\text m$ .
	$=$	$\displaystyle \frac{1}{2}\cdot 30\;\mathrm{m}\cdot 10\;\mathrm{m}+ 30\;\mathrm{m}\cdot 5\;\mathrm{m}$
	↓	Berechne.
	$=$	$\displaystyle 300\text m^2$

Da es sowohl eine Vorder- als auch eine Rückseite gibt, die den gleichen Flächeninhalt haben, kannst du die Fläche mal 2 nehmen.

\displaystyle A_{\text{Spitzdach Vorderseite und Rückseite}}=2\cdot 300\;\mathrm{m}^2=600\;\mathrm{m}^2

Jetzt fehlen noch zwei kleine Seiten vom Vordach, mit der Länge $10\;\mathrm{m}$ und Breite $5\;\mathrm{m}$ .

$\displaystyle A_{Seitenflächen}$	$=$	$\displaystyle 2\cdot l\cdot b$
	↓	Setze die gegebenen Werte ein: $l=10\text m$ und $b=5\text m$
	$=$	$\displaystyle 2\cdot10\text{m}\cdot5\text{m}\$
	$=$	$\displaystyle 100\text{m}^2$

Gesamtfläche Dach

\displaystyle \def\arraystretch{1.25} \begin{array}{rcl}O_{gesamt}&=&O_{Seitendächer}\\&&+A_{SpitzdachOberseite}\\&&+A_{SpitzdachVorderseiteundRückseite}\\&&+A_{Seitenflächen}\end{array}

Setze die Werte ein. Am besten die genauen, ungerundeten Werte, ansonsten auf zwei Nachkommastellen gerundet.

\displaystyle \def\arraystretch{1.25} \begin{array}{rcl}O_{gesamt}&=&4100\;\mathrm{m}^2\\&&+2163{,}33\;\mathrm{m}^2\\&&+600\;\mathrm{m}^2\\&&+100\;\mathrm{m}^2\\&=&6963{,}33\;\mathrm{m}^2\end{array}

Es wird also insgesamt so viel Farbe benötigt, dass sie für eine Fläche von $6963{,}33\;\mathrm{m}^2$ reicht.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Wie viele $10\;\mathrm{l}$ Eimer Farbe werden für den ganzen Tempel benötigt, wenn ein Liter für $7\;\mathrm{m}^2$ reicht.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle M_{\text{Säule}}$	$=$	$\displaystyle U\cdot h$
	↓	Setze $U=d\cdot \pi$ ein.
	$=$	$\displaystyle d\cdot\pi\cdot h$
	↓	Setze $d=3\ \text{m}\$ und $h=20\ \text{m}\$ ein.
	$=$	$\displaystyle 3\text{m}\cdot\pi\cdot20\text{m}\$
	$=$	$\displaystyle 60\ \pi\ \text{m}^2$
	$\approx ≈$	$\displaystyle 188{,}50\ \text{m}^2$

$\displaystyle M_{\text{Säulen}\ }$	$=$	$\displaystyle 25\cdot M_{\text{Säule}}$
	↓	Rechne mit dem ungerundeten Wert und setze $M_{\text{Säule}}=60 \pi \text{m}^2$ .
	$=$	$\displaystyle 25\cdot60\ \pi\text{m}^2$
	$=$	$\displaystyle 1500\pi\text{m}^2$
	$=$	$\displaystyle 4712{,}39\ \text{m}^2$

$\displaystyle O_{gesamt}$	$=$	$\displaystyle O_{Dach}+O_{Säulen}$
	↓	Setze die Werte aus Teilaufgabe a) und b) ein.
	$\approx ≈$	$\displaystyle 6963{,}33 \;\mathrm{m}^2 + 4712{,}39\;\mathrm{m}^2$
	$=$	$\displaystyle 11 675{,}72\;\mathrm{m}^2$

$\displaystyle x$	$=$	$\displaystyle O_{gesamt}:7\;\mathrm{\frac{{m}^2}{l}}$
	↓	Setze $O_{Gesamt}$ ein.
	$=$	$\displaystyle 11 675{,}72\;\mathrm{m}^2:7\;\mathrm{\frac{{m}^2}{l}}$
	$=$	$\displaystyle 1667{,}96\;\mathrm{l}$

$\displaystyle e$	$=$	$\displaystyle \frac{x}{10\text l}$
	↓	Setze $x$ ein.
	$=$	$\displaystyle \frac{1667{,}96\;\mathrm{l}}{10\;\mathrm{l}}$
	$=$	$\displaystyle 166{,}796$

Berechnung der Mantelfläche einer Säule

Berechnung der Mantelfläche aller Säulen

Hast du eine Frage oder Feedback?

Oberfläche der Seitendächer

Oberfläche Mittelteil

Berechnung der Breite des Seitendachs

Berechnung der Fläche der Oberseite des Spitzdachs

Berechnung der Oberfläche des Spitzdachs vorne

Gesamtfläche Dach

Hast du eine Frage oder Feedback?

Oberfläche Tempel insgesamt

Wie viele Liter sind das?

Wie viele Eimer sind das?

Hast du eine Frage oder Feedback?