1 Übersicht
Inhalt des Kurses
In diesem Kurs lernst du, in welchem Punkt sich zwei Geraden schneiden. Dabei werden die Begriffe des Schnittpunkts sowie des linearen Gleichungssystems (mit zwei Unbekannten) eingeführt. Am Ende kann man ein solches System mithilfe des sogenannten Gleichsetzungsverfahrens lösen.
Vorkenntnisse
Du solltest wissen, was eine lineare Gleichung ist und wie man diese umformen kann. Zudem ist es wichtig, dass du Punkte aus einem Koordinatensystem ablesen und diese wieder einsetzen kannst. Da du dich in diesem Kurs mit Geraden und ihren Gleichungen beschäftigen wirst, solltest du wissen, wie du eine solche Geradengleichung aufstellen und sie zeichnen kannst.
Kursdauer
Dieser Kurs dauert ca. 1,5 Stunden.
2 Ein ungleiches Rennen (1/2)
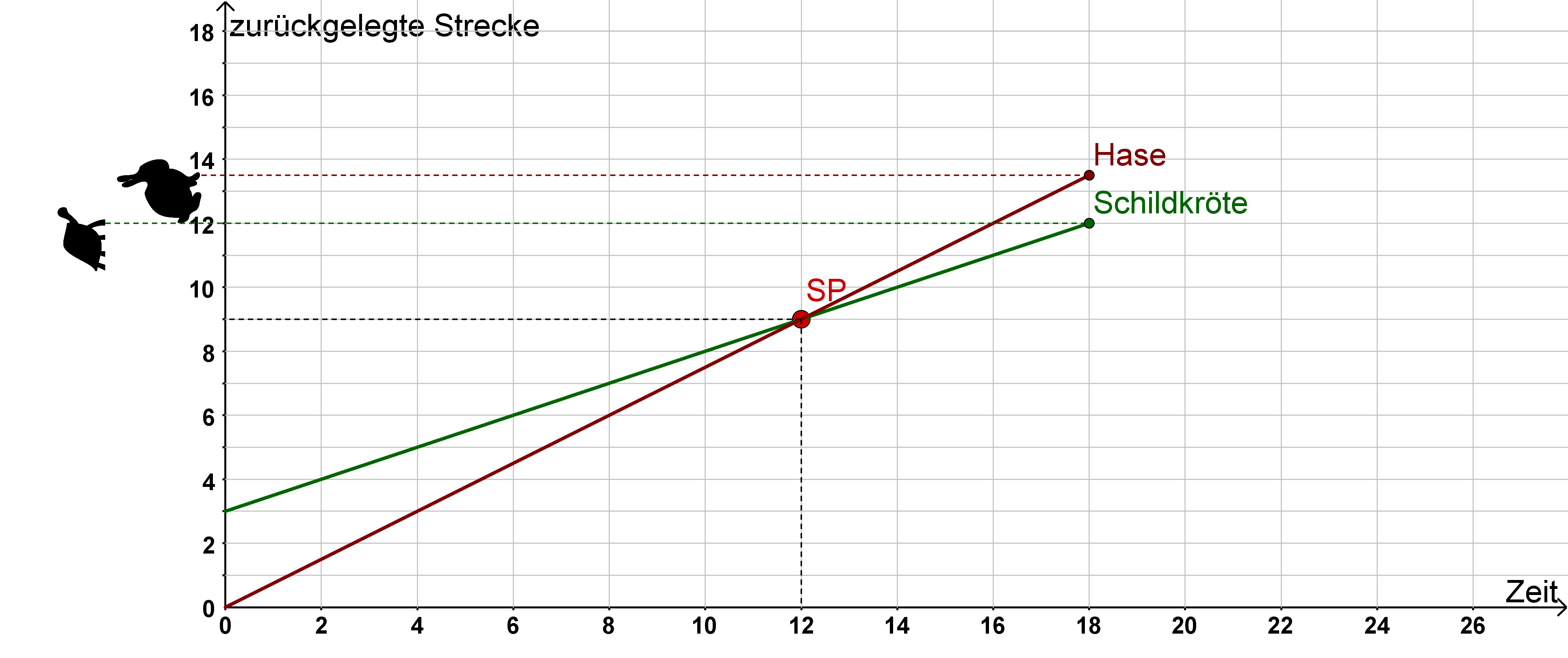
Ein Hase und seine Freundin Schildkröte starten ein Rennen. Der Hase will natürlich, dass das ganze fair bleibt. Deshalb gibt er der Schildkröte, die ja etwas langsamer ist, einen kleinen Vorsprung. Sie darf Meter weiter vorne starten.
Der Hase ist jetzt sehr gespannt. Er weiß nämlich nicht, ob der Vorsprung zu viel war und er die Schildkröte im Rennen nicht einholen wird. Er hofft aber, eine Chance zu haben, und das Rennen zu gewinnen.

3 Ein ungleiches Rennen (2/2)
Klicke auf "Rennen starten!", um dir das Rennen anzuschauen.
Auf der x-Achse siehst du die vergangene Zeit seit dem Startschuss,
auf der y-Achse die bereits zurückgelegte Strecke. Am linken Rand siehst du außerdem die aktuelle Position von Hase und Schildkröte.
4 Was ist ein Schnittpunkt? (1/2)
Wie du anhand der Animation beobachten konntest, konnte der Hase die Schildkröte überholen. Auf ihrer Rennstrecke gibt es also einen Treffpunkt der beiden. Dieser Punkt ist somit die Antwort zu der Frage:
"Wann und wo treffen sich die Tiere?"
Die Antwort zu dieser Frage wirst du in diesem Kurs auf verschiedene Arten finden.
Denkaufgabe
Stelle für die Graphen von Schildkröte und Hase aus der Geschichte die linearen Funktionsgleichungen auf.
5 Was ist ein Schnittpunkt? (2/2)
Da Punkte im Koordinatensystem immer mit und ausgedrückt werden, werden die Achsen "Zeit" als -Achse und "zurückgelegte Strecke" als -Achse festgelegt.
Die Geradengleichungen aus der Geschichte sehen nun so aus:
Schildkröte:
Hase:
Der Punkt, an dem sich zwei Geraden kreuzen, ist also der oben genannte Treffpunkt. Diesen nennt man in der Mathematik einen Schnittpunkt. Indem du den Schnittpunkt am Graphen abliest, findest du die Lösung zum Problem heraus.
Überprüfe den Schnittpunkt
Wenn du einen Schnittpunkt aus der Graphik abgelesen hast, kannst du ihn in deine zwei Geradengleichungen einsetzen, um ihn zu überprüfen. Die Koordinaten des Schnittpunktes lauten .
Schildkröte:
Hase:
Setze die Koordinaten des Schnittpunkts ein.
Schildkröte:
Hase:
Erhältst du zwei wahre Aussagen, so hast du den richtigen Schnittpunkt abgelesen.
Schildkröte:
Hase:
Da in beiden Gleichungen nach dem Auflösen eine wahre Aussage entsteht, hast du den Schnittpunkt richtig bestimmt.
6 Beispielaufgabe zum Schnittpunkt
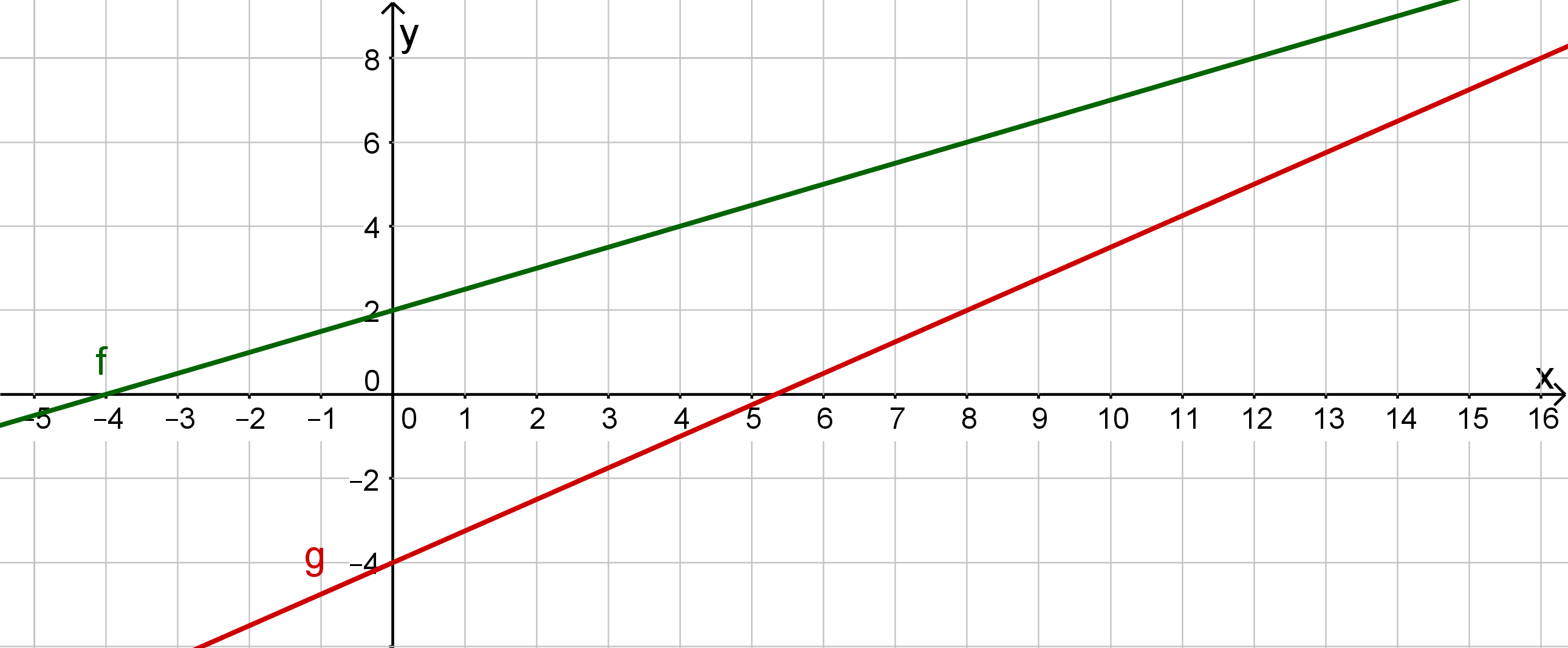
Nun machen der Hase und die Schildkröte erneut ein Wettrennen, diesmal hat die Schildkröte aber einen Vorsprung von .
Die Geradengleichung für die Schildkröte und die Geradengleichung für den Hasen sind jetzt gegeben durch:
Schildkröte:
Hase:
Wir wollen wieder herausfinden, zu welchem Zeitpunkt der Hase die Schildkröte überholt.
a) Zeichne die Geradengleichungen in das Koordinatensystem.
b) Lies aus der Zeichnung den Schnittpunkt ab.
c) Interpretiere den Schnittpunkt im Sachzusammenhang.
7 Übungsaufgaben zum Schnittpunkt
Laden
Laden
8 Was ist ein lineares Gleichungssystem (LGS)?
Lässt der Hase seiner Freundin zu Beginn einen zu großen Vorsprung, kann es sein, dass der Hase die Schildkröte niemals überholt oder der Treffpunkt so spät ist, dass dein Heft nicht lang genug ist, um den Treffpunkt einzuzeichnen. Die graphische Lösung ist daher nicht immer gut und sinnvoll.
Wie gehst du in solch einem Fall vor?
Du hast in der Geschichte mit zwei Geraden gearbeitet, deren Gleichungen du kennst. Eine mögliche Schreibweise für ein Gleichungssystem ist, dass du die Gleichungen untereinander schreibst und mit römischen Ziffern nummerierst. So sieht das aus:
Was ist ein LGS?
Eine lineare Gleichung ist von einer oder mehreren Unbekannten (Variablen), zum Beispiel und abhängig.
Mehrere lineare Gleichungen mit denselben Unbekannten (Variablen), zum Beispiel und , stellen ein System von linearen Gleichungen dar. Das Ziel ist, Werte für die Unbekannten zu finden, sodass alle Gleichungen gleichzeitig erfüllt sind.
9 Warum brauchst du Lösungsverfahren?
Wie auf der letzten Folie erwähnt, kann man die Lösung, also den Schnittpunkt, nicht immer graphisch ablesen.
In diesem Fall kannst du die Lösung ausrechnen.
Um zu verstehen, wie die verschiedenen Lösungsverfahren funktionieren, solltest du dir zuerst überlegen, was das Besondere am Schnittpunkt ist.
Denkaufgabe
Was macht einen Schnittpunkt aus?
10 Zwei Geraden - ein gemeinsamer Punkt!
Graphische Besonderheit
Der Schnittpunkt liegt auf beiden Geraden.
Für den -Wert des Schnittpunktes liefern beide Geraden den gleichen -Wert.
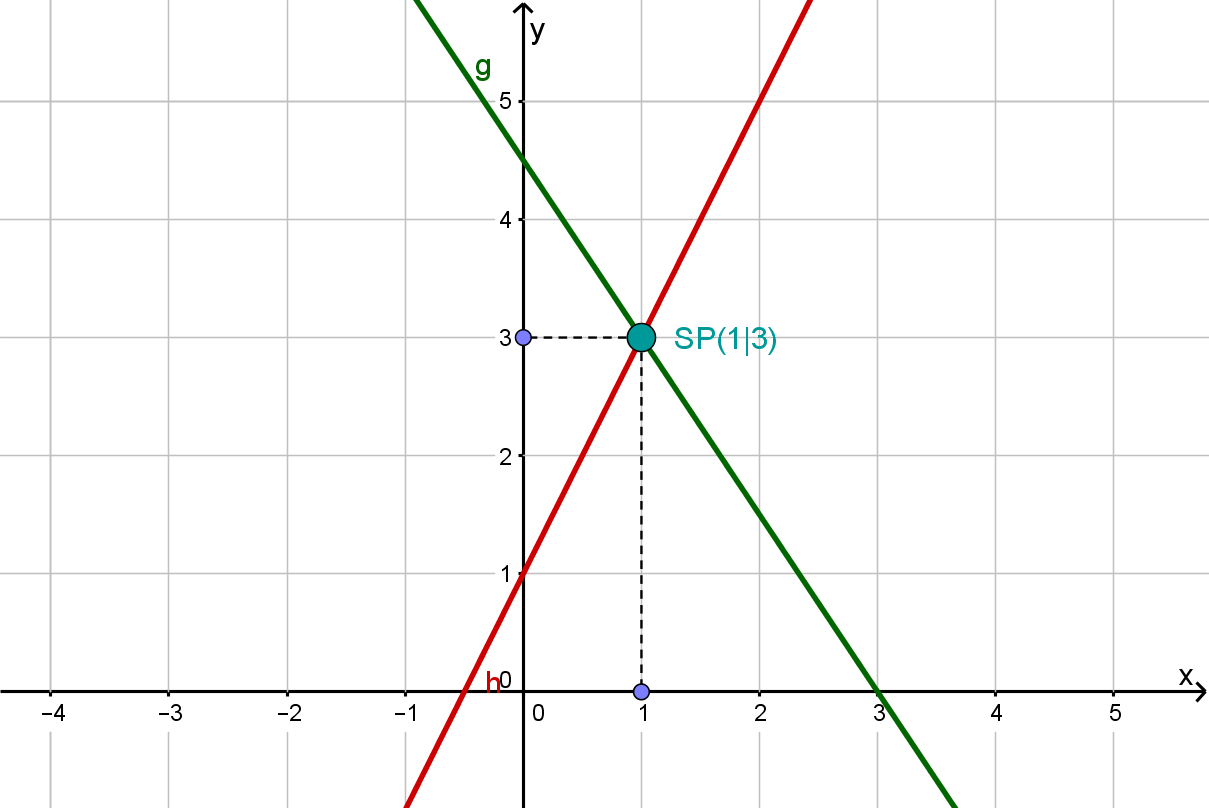
Rechnerische Besonderheit
Am Schnittpunkt sind beide Gleichungen des Gleichungssystems erfüllt!
Wenn du also den Schnittpunkt in beide Gleichungen einsetzt, bekommst du die gleiche, wahre Aussage!
Schnittpunkt:
Gerade g:
Gerade h:
11 Gleichsetzungsverfahren (1/2)
Der Schnittpunkt ist also ein Punkt, der auf beiden Geraden liegt. Dies kannst du ausnutzen, um den Schnittpunkt der beiden Funktionen auszurechnen.
Das Verfahren, das hierzu verwendet wird, heißt Gleichsetzungsverfahren.
Wie funktioniert das Gleichsetzungsverfahren?
Betrachte als Beispiel zwei Geraden aus den vorherigen Folien des Kurses. Schreibe diese als lineares Gleichungssystem auf:
Da du einen Punkt suchst, in dem die beiden -Werte gleich sind, muss jeweils auch der rechte Teil der Gleichung denselben Wert haben:
Nun kannst du die beiden rechten Seiten gleichsetzen:
Übungsaufgabe
Löse nach auf!
12 Gleichsetzungsverfahren (2/2)
13 Das Gleichsetzungsverfahren - Schritt für Schritt!
Du hast gerade gesehen, wie das Gleichsetzungsverfahren in einem bestimmten Beispiel angewendet wurde. Nun wird nochmal allgemein betrachtet, wie das Verfahren funktioniert.
Grundvoraussetzung
Die beiden Gleichungen in deinem Gleichungssystem müssen beide nach dem gleichen Term aufgelöst sein! In diesem Term sollte eine Unbekannte (oft oder ) vorkommen, die dann nicht mehr auf der anderen Seite steht.
Beispiel 1
Beispiel 2
1. Schritt
Setze die beiden Seiten der Gleichungen zusammen, die nicht gleich sind.
Beispiel 1
Beispiel 2
2. Schritt
Löse nach der verbliebenen Unbekannten auf.
Beispiel 1
Beispiel 2
3. Schritt
Setze in eine der beiden Gleichungen ein.
Beispiel 1
In :
Beispiel 2
In :
14 Beispielaufgabe zum Gleichsetzungsverfahren (1/2)
Gegeben ist das lineare Gleichungssystem
Berechne die Koordinaten des Schnittpunktes der zwei Geraden, indem du dazu das Gleichsetzungsverfahren benutzt!
Lösung
Um das Gleichsetzungsverfahren anzuwenden, musst du die beiden Gleichungen entweder nach oder nach auflösen. Da eine Geradengleichung die Form hat, löst du die Gleichungen nach auf.
Denke dabei daran, wie du Gleichungen umformen darfst.
Auflösung nach einer Variablen
15 Beispielaufgabe zum Gleichsetzungsverfahren (2/2)
Anwendung des Gleichsetzungsverfahrens
Das Gleichsetzungsverfahren sorgt dafür, dass von zwei Unbekannten nur noch eine übrig bleibt. Dafür hast du gerade beide Gleichungen nach der Unbekannten aufgelöst. Diese Gleichungen kannst du nun gleichsetzen, da bei einem linearen Gleichungssystem (LGS) die Unbekannten und beide Gleichungen und erfüllen.
Setze nun in oder ein. Damit das Ausrechnen einfacher ist, nimm die erste Gleichung.
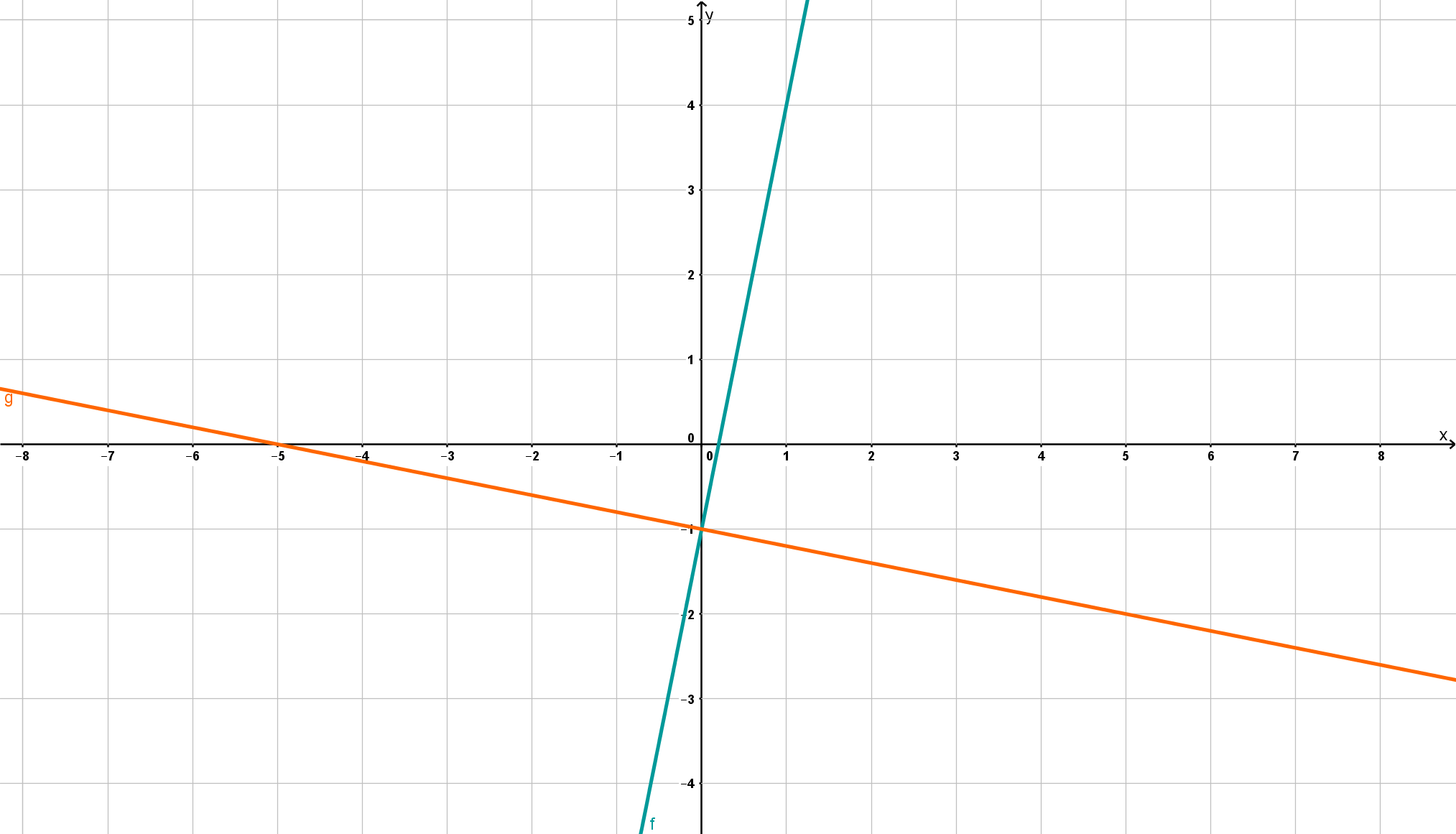
Der Schnittpunkt der zwei Gleichungen ist .
Um zu überprüfen, ob dein ausgerechneter Schnittpunkt auch stimmt, kannst du die Geraden zeichnen. Rechts siehst du, wo sie sich kreuzen.
16 Übungsaufgaben zum Gleichsetzungsverfahren
Laden
Laden
17 Zusammenfassung
Schnittpunkt
Du hast in diesem Kurs gelernt, was ein Schnittpunkt ist und wie man ihn abliest.
In einem Schnittpunkt schneiden sich zwei Geraden, beide Geradengleichungen sind gleichzeitig erfüllt.
Lineares Gleichungssystem
Du weißt jetzt, dass ein lineares Gleichungssystem (LGS) aus zwei (oder mehreren) linearen Gleichungen besteht. Diese Gleichungen hängen jeweils von den gleichen Unbekannten (meist und ) ab.
Die Gleichungen nummerierst du mit römischen Ziffern, damit du die Übersicht nicht verlierst.
Du suchst die Lösung des linearen Gleichungssystems, das ist der Punkt , an dem alle Gleichungen wahre Aussagen liefern. Das bedeutet: Wenn du den Punkt in die Gleichungen einsetzt, kommt so etwas heraus, wie . (Hinweis: Setze und in das obige LGS ein.)
Wenn du alle Gleichungen des LGS in Geradengleichungen der Form umformst, ist die Lösung des Gleichungssystems genau der Schnittpunkt dieser Geraden.
Gleichsetzungsverfahren
Wenn du den Schnittpunkt nicht oder nicht genau ablesen kannst, so kannst du diesen ausrechnen. Dazu verwendest du das Gleichsetzungsverfahren, welches dir in drei Schritten die Lösung des LGS liefert:
Gleichsetzen: Setze die Gleichungen und gleich.
Auflösen: Löse die entstandene Gleichung nach einer Variablen auf.
Einsetzen: Durch Einsetzen in die Gleichung oder erhältst du den Wert der anderen Variablen.
18 Zeig, was du kannst!
Laden
