Teil B - lernen mit Serlo!

Dieser Inhalt wurde gelöscht.

Lösung zur Teilaufgabe B 1.1

In dieser Teilaufgabe beschäftigst du dich mit dem Definitions- und Wertebereich einer Exponentialfunktion.

Wie du vielleicht weißt, ist der maximale Definitionsbereich einer Exponentialfunktion ganz $ℝ$ .

Der maximale Wertebereich einer Exponentialfunktion $f (b) = a^{b}$ ist

$ℝ^{+}$ falls $a > 0$ und
$ℝ^{-}$ falls $a < 0$ .

An der $- 3$ in der Funktionsgleichung siehst du, dass die Exponentialfunktion $f_{1} : y = {0,75}^{x + 2} - 3$ im Vergleich zur Funktionsgleichung $y = {0,75}^{x + 2}$ lediglich um $3$ Einheiten nach unten verschoben ist.

Es gilt also ebenfalls $𝔻 = ℝ$ .

Da bei der Exponentialfunktion $y = {0,75}^{x + 2}$ die Basis $a = 0,75$ größer als Null ist, ist der maximale Wertebereich von $y = {0,75}^{x + 2}$ durch $ℝ^{+}$ gegeben.

Folglich ist $𝕎 = {y | y > - 3}$ der Wertebereich der um drei Einheiten nach unten verschobenen Funktion $f_{1} : y = {0,75}^{x + 2} - 3$ .

Um den Graphen der Funktion in das Koordinatensystem einzuzeichnen, berechnest du zunächst einige Punkte, die du anschließend in ein Koordinatensystem eintragen kannst.

Eine mögliche Wertetabelle ist:

Nun kannst du den Graph der Funktion $f_{1}$ in ein Koordinatensystem einzeichnen.

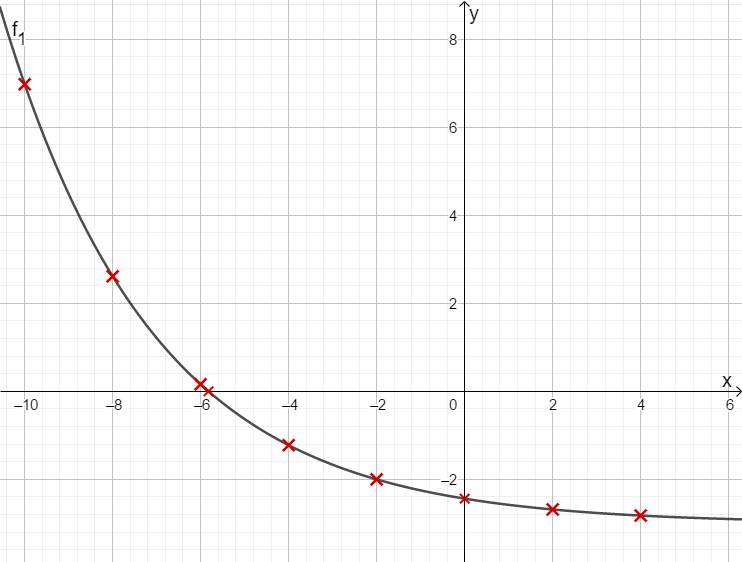
Lösung zur Teilaufgabe B 1.2

Zunächst wendest du die orthogonale Affinität mit der $x$ -Achse als Affinitätsachse und $k = - 2$ als Affinitätsmaßstab auf die Funktion $f_{1}$ an. Dann folgt

(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{c} x \\ - 2 \cdot ({0,75}^{x + 2} - 3) \end{array})

und damit

$y^{'} = - 2 \cdot {0,75}^{x^{'} + 2} + 6$ .

Parallelverschiebung mit dem Vektor $\vec{v} = (\begin{array}{c} - 2 \\ 1 \end{array})$ liefert

(\begin{array}{c} x^{''} \\ y^{''} \end{array}) = (\begin{array}{c} x^{'} \\ - 2 \cdot {0,75}^{x^{'} + 2} + 6 \end{array}) + (\begin{array}{c} - 2 \\ 1 \end{array}) = (\begin{array}{c} x^{'} - 2 \\ - 2 \cdot {0,75}^{x^{'} + 2} + 7 \end{array})

Es gilt also $y^{''} = - 2 \cdot {0,75}^{x^{'} + 2} + 7$ .

Mit $x^{''} = x^{'} - 2$ folgt $x^{'} = x^{''} + 2$ und damit

$y^{''} = - 2 \cdot {0,75}^{x^{''} + 4} + 7$ .

Insgesamt folgt also:

f_{2} : y = - 2 \cdot {0,75}^{x + 4} + 7

Um den Graphen der Funktion in das Koordinatensystem einzuzeichnen, berechnest du zunächst einige Punkte, die du anschließend in ein Koordinatensystem eintragen kannst.

Eine mögliche Wertetabelle ist:

Nun kannst du die Funktion $f_{2}$ in dein Koordinatensystem einzeichnen.

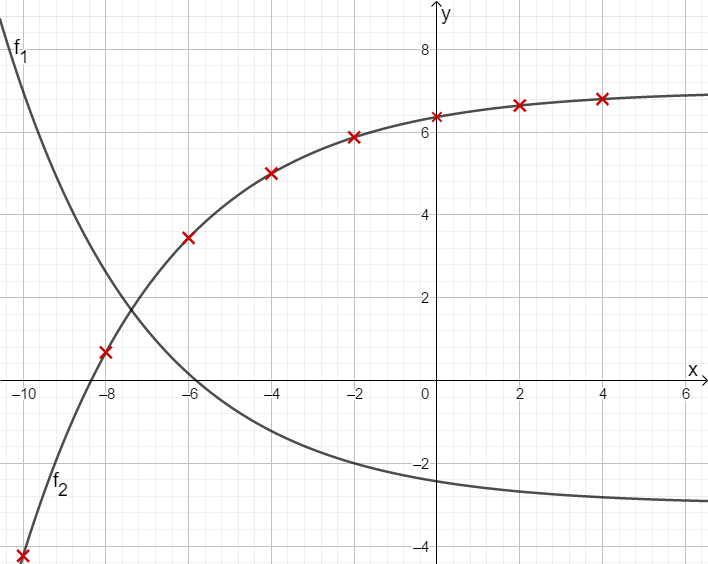
Lösung zur Teilaufgabe B 1.3

In dieser Teilaufgabe berechnest du Punkte eines Drachenvierecks und zeichnest diese anschließend in ein Koordinatensystem ein.

Nun sollst du die beiden Drachenvierecke $A_{1} B_{1} C_{1} D_{1}$ und $A_{2} B_{2} C_{2} D_{2}$ in dein Koordinatensystem einzeichnen. Dafür musst du die Punkte $A_{1}, B_{1}, C_{1}, D_{1}$ und $A_{2}, B_{2}, C_{2}, D_{2}$ bestimmen.

Um den Punkt $A_{1}$ zu berechnen, setzt du $x = - 5$ in $A_{n} (x | {0,75}^{x + 2} - 3)$ ein und erhältst ungefähr $A_{1} (- 5 | - 0,63)$ . Für den Punkt $C_{1}$ setzt du $x = - 5$ in $C_{n} (x | - 2 \cdot {0,75}^{x + 4} + 7)$ ein und erhältst den gerundeten Punkt $C_{1} (- 5 | 4,33)$ .

Die Punkte $A_{2}$ und $C_{2}$ berechnest du analog, indem du $x = 1$ in $A_{n} (x | {0,75}^{x + 2} - 3)$ und $C_{n} (x | - 2 \cdot {0,75}^{x + 4} + 7)$ einsetzt.

Dies liefert ungefähr $A_{2} (1 | - 2,58)$ und $C_{2} (1 | 6,53)$ .

Außerdem weißt du aus der Angabe, dass $\vec{A_{n} B_{n}} = (\begin{array}{c} 3 \\ 2 \end{array})$ gilt, insbesondere also auch $\vec{A_{1} B_{1}} = (\begin{array}{c} 3 \\ 2 \end{array})$ und $\vec{A_{2} B_{2}} = (\begin{array}{c} 3 \\ 2 \end{array})$ .

Damit erhältst du die gerundeten Ergebnisse

\vec{B_{1}} = \vec{A_{1}} + (\begin{array}{c} 3 \\ 2 \end{array}) = (\begin{array}{c} - 5 \\ - 0,63 \end{array}) + (\begin{array}{c} 3 \\ 2 \end{array}) = (\begin{array}{c} - 2 \\ 1,37 \end{array}) \Rightarrow B_{1} (- 2 | 1,37)

sowie

\vec{B_{2}} = \vec{A_{2}} + (\begin{array}{c} 3 \\ 2 \end{array}) = (\begin{array}{c} 1 \\ - 2,58 \end{array}) + (\begin{array}{c} 3 \\ 2 \end{array}) = (\begin{array}{c} 4 \\ - 0,58 \end{array}) \Rightarrow B_{2} (4 | - 0,58)

Laut Angabe gilt zudem, dass $[A_{n} C_{n}]$ auf den Symmetrieachsen der Drachenvierecke $A_{n} B_{n} C_{n} D_{n}$ liegen, insbesondere liegen also auch $[A_{1} C_{1}]$ auf $A_{1} B_{1} C_{1} D_{1}$ und $[A_{2} C_{2}]$ auf $A_{2} B_{2} C_{2} D_{2}$ .

Folglich liegen $D_{1}$ und $D_{2}$ bezüglich der Symmetrieachsen $[A_{1} C_{1}]$ bzw. $[A_{2} C_{2}]$ symmetrisch zu $B_{1}$ bzw. $B_{2}$ . Dies bedeutet, dass $B_{n}$ und $D_{n}$ jeweils die gleichen $y$ -Koordinaten haben. Du erhältst $D_{n}$ also, indem du $B_{n}$ an der im Bild rot gestrichelten Spiegelachse $A_{n} C_{n}$ spiegelst.

Nun kannst du alle Punkte und anschließend die Drachenvierecke $A_{1} B_{1} C_{1} D_{1}$ und $A_{2} B_{2} C_{2} D_{2}$ in dein Koordinatensystem einzeichnen. Dies sollte wie folgt aussehen:

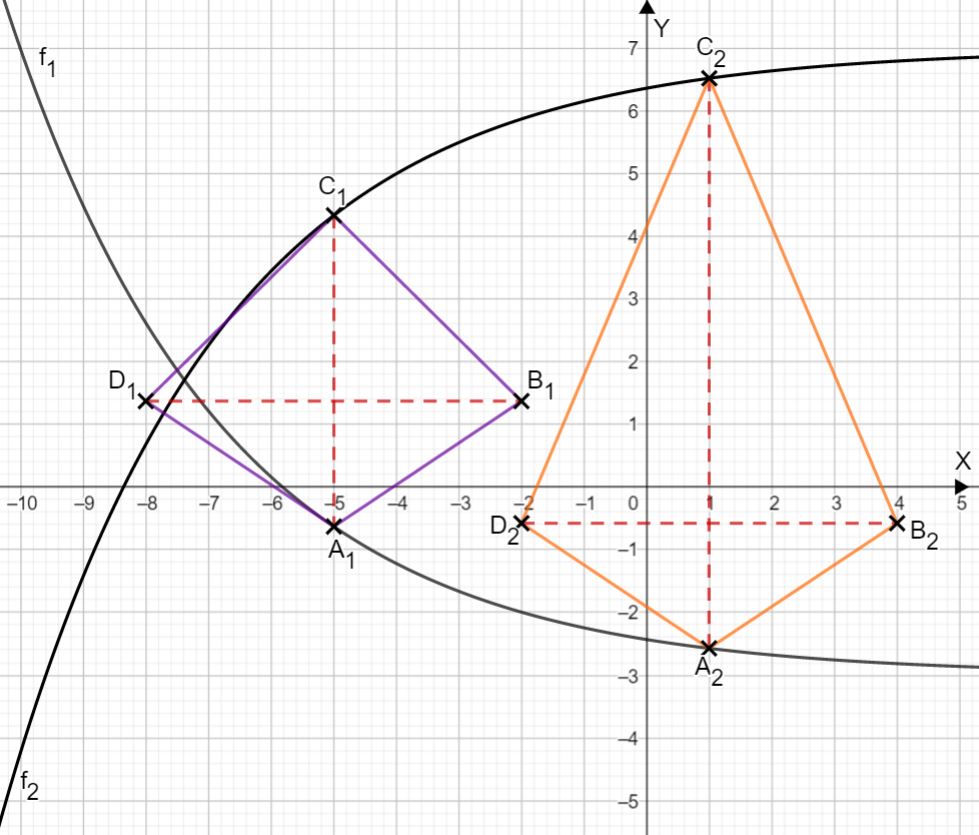
Skizze der Funktionen und Drachenvierecke

Lösung zur Teilaufgabe B 1.4

In dieser Teilaufgabe geht es um die Berechnung der Länge einer Strecke zwischen zwei Punkten.

Um die Länge der Strecke $[A_{n} C_{n}]$ zu berechnen, bemerkst du zunächst, dass die Punkte $A_{n}$ und $C_{n}$ dieselbe $x$ -Koordinate besitzen, also "untereinander" liegen, wobei jeweils $C_{n}$ der obere und $A_{n}$ der untere Punkt ist.

Den Abstand dieser zwei Punkte berechnest du nun, indem du die $y$ -Koordinate des Punktes $A_{n}$ von der $y$ -Koordinate des Punktes $C_{n}$ abziehst.

Es gilt also

$A_{n} C_{n} (x)$	$=$	$[- 2 \cdot {0,75}^{x + 4} + 7 - ({0,75}^{x + 2} - 3)]$
	↓	Ersetze $x + 4$ durch $x + 2 + 2$ .
	$=$	$[- 2 \cdot {0,75}^{x + 2 + 2} + 7 - ({0,75}^{x + 2} - 3)]$
	↓	${0,75}^{x + 2 + 2} = {0,75}^{x + 2} \cdot {0,75}^{2}$
	$=$	$[- 2 \cdot {0,75}^{2} \cdot {0,75}^{x + 2} + 7 - ({0,75}^{x + 2} - 3)]$
	↓	Vereinfache
	$=$	$[- 1,125 \cdot {0,75}^{x + 2} + 7 - ({0,75}^{x + 2} - 3)]$
	↓	Klammern auflösen
	$=$	$[- 1,125 \cdot {0,75}^{x + 2} + 7 - 1 \cdot {0,75}^{x + 2} + 3]$
	↓	Klammere ${0,75}^{x + 2}$ aus
	$=$	$[{0,75}^{x + 2} \cdot (- 1,125 - 1) + 7 + 3]$
	↓	Vereinfache
	$=$	$[- 2,125 \cdot {0,75}^{x + 2} + 10]$

Es ist also $A_{n} C_{n} (x) = [- 2,125 \cdot {0,75}^{x + 2} + 10] (LE)$ .

Lösung zur Teilaufgabe B 1.5

In dieser Teilaufgabe berechnest du die Koordinaten eines Punktes einer Raute.

Für die Raute $A_{3} B_{3} C_{3} D_{3}$ gilt $A_{3} C_{3} = 4 (LE)$ .

Aus Teilaufgabe B. 1.4 weißt du, dass $A_{n} C_{n} (x) = [- 2,125 \cdot {0,75}^{x + 2} + 10] (LE)$ gilt.

Damit folgt nun $- 2,125 \cdot {0,75}^{x + 2} + 10 = 4$

Jetzt kannst du die Gleichung nach $x$ auflösen. Dafür benötigst du die Rechenregeln des $\ln$ .

Auflösen liefert:

$- 2,125 \cdot {0,75}^{x + 2} + 10$	$=$	$4$	$- 10$
$- 2,125 \cdot {0,75}^{x + 2}$	$=$	$- 6$	$: (- 2,125)$
${0,75}^{x + 2}$	$=$	$\frac{- 6}{- 2,125}$	$\ln (\cdot)$
$\ln ({0,75}^{x + 2})$	$=$	$\ln (\frac{- 6}{- 2,125})$
	↓	Wende Rechenregel des $\ln$ an.
$(x + 2) \cdot \ln (0,75)$	$=$	$\ln (\frac{- 6}{- 2,125})$	$: \ln (0,75)$
$(x + 2)$	$=$	$\frac{\ln (\frac{- 6}{- 2,125})}{\ln (0,75)}$	$- 2$
$x$	$=$	$\frac{\ln (\frac{- 6}{- 2,125})}{\ln (0,75)} - 2$
	↓	Vereinfache
	$=$	$- 5,60811 \dots$
	↓	Runde
	$\approx$	$- 5,61$

Die $x$ -Koordinate des Punktes $A_{3}$ ist also $x = - 5,61$ .

Die $y$ -Koordinate von $A_{3}$ erhältst du durch Einsetzen von $x = - 5,61$ in $A_{n} (x | {0,75}^{x + 2} - 3)$ .

Dies liefert ${0,75}^{- 5,61 + 2} - 3 = - 0,174932 = - 0,17$ als $y$ -Koordinate.

Mit $\vec{A_{3} B_{3}} = (\begin{array}{c} 3 \\ 2 \end{array})$ folgt nun

\vec{O B_{3}} = \vec{O A_{3}} + \vec{A_{3} B_{3}} = (\begin{array}{c} - 5,61 \\ - 0,17 \end{array}) + (\begin{array}{c} 3 \\ 2 \end{array}) = (\begin{array}{c} - 2,61 \\ 1,83 \end{array}) .

Damit ist der Punkt $B_{3}$ durch $B_{3} (- 2,61 | 1,83)$ gegeben.

Lösung zur Teilaufgabe B 1.6

In dieser Aufgabe berechnest du den Flächeninhalt eines Drachenvierecks.

Der Flächeninhalt eines Drachenvierecks $A B C D$ wird durch $A = \frac{e \cdot f}{2} = \frac{A C \cdot B D}{2}$ berechnet.

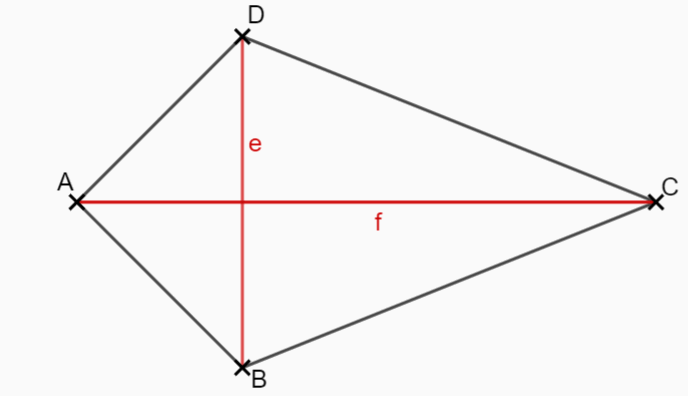
Nun kannst du den Flächeninhalt der Drachenvierecke $A_{n} B_{n} C_{n} D_{n}$ berechnen:

In Teilaufgabe B. 1.4 hast du $A_{n} C_{n} (x) = [- 2,125 \cdot {0,75}^{x + 2} + 10] (LE)$ berechnet.

Weil $D_{n}$ bezüglich der Symmetrieachse $[A_{n} C_{n}]$ symmetrisch zu $B_{n}$ ist und $\vec{A_{n} B_{n}} = (\begin{array}{c} 3 \\ 2 \end{array})$ gilt, folgt $B_{n} D_{n} = 6 (LE)$

Damit erhältst du

$A (x)$	$=$	$\frac{(- 2,125 \cdot {0,75}^{x + 2} + 10) \cdot 6}{2}$
	↓	Löse die Klammer auf.
	$=$	$\frac{- 12,75 \cdot {0,75}^{x + 2} + 60}{2}$
	↓	Kürze.
	$=$	$- 6,375 \cdot {0,75}^{x + 2} + 30$

Es ist also $A (x) = - 6,375 \cdot {0,75}^{x + 2} + 30 (FE)$ .

Da der Termwert von $- 6,375 \cdot {0,75}^{x + 2}$ für alle $x \in ℝ$ negativ ist, gilt für den Flächeninhalt der Drachenvierecke $A_{n} B_{n} C_{n} D_{n}$ immer $A < 30 (FE)$ . Insbesondere gilt dies also auch für alle $x > - 6,61$ .

Wenn du möchtest, kannst du dir im folgenden Video noch eine Schritt-für-Schritt-Lösung der Aufgabe ansehen.

Laden

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?