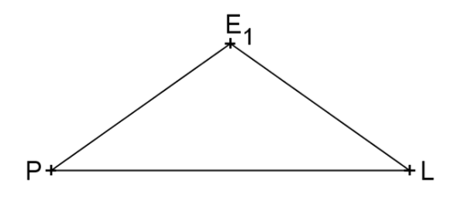
Deine neuen Dreiecke sollen gleichschenklig sein, den gleichen Flächeninhalt wie das Dreieck haben und die Strecke soll eine der Seiten sein.
Überlege dir nun als erstes, wann zwei Dreiecke mit gleicher Grundseite den gleichen Flächeninhalt haben: Den Flächeninhalt eines Dreiecks berechnet man, indem man Grundseite mit der Höhe und mulipliziert. Wenn man die Länge der Grundseite gleich lässt (du nimmst hier genau die gleiche Grundseite) und man den gleichen Flächeninhalt erhalten will, muss man also auch die Höhe gleich lassen.
Zusätzlich willst du noch, dass die Dreiecke gleichschenklig sind. Welche Rollen kann dann die Strecke erfüllen? Sie kann entweder die Seite sein, die es einmal gibt, dann müssen die anderen beiden Seiten gleich lang sein. Alternativ kann es die Seite sein, die es von der Länge doppelt gibt.
Die erste Möglichkeit ist die leichter sichtbare: Du willst also ein Dreieck mit als Grundseite, der gleichen Höhe wie das ursprüngliche Dreieck und schließlich sollen die neuen beiden Seiten beide gleich lang sein. Das heißt, du musst das Dreieck und damit auch den Punkt an spiegeln.
Dafür zeichnest du zwei Kreise mit den Mittelpunkten und jeweils durch den Punkt . Der zweite Schnittpunkt der beiden Kreise ist der Punkt . Diese Konstruktion kannst du auch in dem Applet nachvollziehen, ziehe dazu einfach den Schieberegler nach rechts.
Bei der anderen Variante brauchst du wieder ein Dreieck mit der Grundseite , der Höhe des ursprünglichen Dreiecks und nur soll diesmal eine der anderen Seiten genau so lang sein wie .
Dafür zeichnest du dir als erstes eine Parallele zu durch den Punkt . Damit stellst du sicher, dass das Dreieck die richtige Höhe haben wird. Anschließend zeichnest du mit dem Zirkel einen Kreis oder mit einem Radius von , um zu erreichen, dass es eine weitere Seite mit der Länge gibt. Der Punkt ist der Schnittpunkt zwischen der Gerade und dem Kreis.