Gruppe A

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Vereinfache jeweils so weit wie möglich.
1. $\frac 1 2 \cdot 12 \cdot 0{,}2 \cdot 5=$
  Punkte: 1
  
  Teilaufgabe a)
  Es gibt hier sehr viele unterschiedliche Möglichkeiten, in welcher Reihenfolge man das Produkt berechnen kann. Also kann es sehr gut sein, dass du einen anderen, genauso richtigen Weg gewählt hast.
  Berechne zuerst $\frac12\cdot12$ . Dazu brauchst du die Multiplikation von eines Bruchs mit einer natürlichen Zahl.
  Als nächstes kannst du zum Beispiel geschickterweise $0{,}2\cdot5$ rechnen. Vielleicht siehst du nämlich schon, dass $0{,}2=\frac15$ ist. Wenn nicht kannst du die Regeln für die Multiplikation von Dezimalbrüchen verwenden.
  Jetzt kannst du das Ergebnis ausrechnen: $6$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $(2a)^3\cdot a^2=$
  Punkte: 1
  
  Teilaufgabe b)
  Schreibe die Potenzen aus, um alle 2er und alle Variablen miteinander zu multiplizieren.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
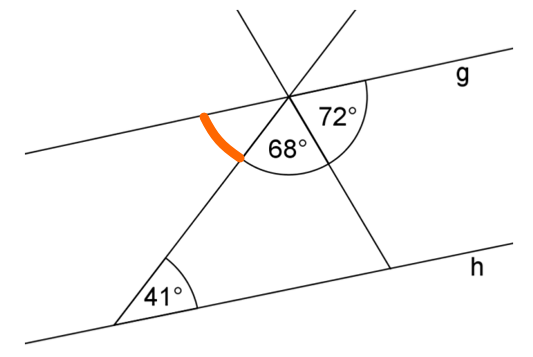
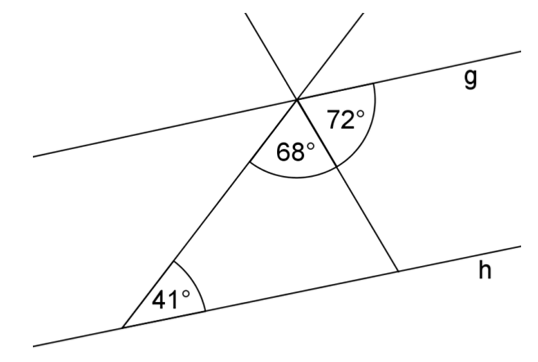
Sind die Geraden $g$ und $h$ zueinander parallel? Begründe deine Antwort und beziehe dabei rechnerische Überlegungen mit ein. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel
Wenn die Geraden $g$ und $h$ parallel wären, würden der Winkel mit $41°$ und sein Wechselwinkel (orange markiert) die gleiche Größe besitzen.
Du musst also nachrechnen, wie groß der orangene Winkel ist.
Nebenwinkel ergeben zusammen $180°$ . Also kann man die beiden anderen Winkel abziehen und man erhält die Größe des orangen Winkels:
$180^\circ-68^\circ-72^\circ=40^\circ$
Du stellst also fest, dass der orangene Winkel $40^\circ\neq41^\circ$ hat. Damit können der $41°$ Winkel und der orangene Winkel keine Wechselwinkel sein und deswegen sind die Geraden $g$ und $h$ nicht parallel.
3
Im Jahr $2014$ hat der Kenianer Dennis Kimetto in Berlin einen neuen Weltrekord im Marathonlauf (Streckenlänge: $42{,}195$ km) aufgestellt. Er ist die Strecke in $2$ Stunden, $2$ Minuten und $57$ Sekunden gelaufen.
Weise nach, dass Kimetto die Strecke in $7377$ Sekunden gelaufen ist, und schätze mithilfe einer Überschlagsrechnung ab, wie viele Meter er dabei im Schnitt pro Sekunde zurückgelegt hat. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zeiteinheiten umrechnen
Sekunden ausrechnen
Rechne die Stunden und Minuten in Sekunden um und rechne alles zusammen.
Meter pro Sekunde abschätzen
Runde die Angaben auf geeignete Werte und rechne das Ergebnis aus.
$\def\arraystretch{1.25} \begin{array}{rl}42{,}195\;km&\approx&42000\;m\\7377\;s&\approx&7000\;s\end{array}$
Wenn du ausrechnen willst, wie viele Meter er im Schnitt pro Sekunde zurückgelegt hat, musst du die Meter durch die Sekunden teilen:
$42000\;m\;:\;7000\;s\;=6\;\frac ms$
Er legt also durchschnittlich $6\;\frac ms$ zurück.
4
Aus einem Lexikon: „Eine natürliche Zahl wird vollkommene Zahl genannt, wenn sie gleich der Summe ihrer (positiven) Teiler außer sich selbst ist.“
Zeige, dass die Zahl $6$ eine vollkommene Zahl ist. (1 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Teilermenge
Finde alle Teiler von $6$ :
Da die Summe aller Teiler außer $6$ selbst $6$ ergibt, handelt es sich bei $6$ um eine vollkommene Zahl.
5
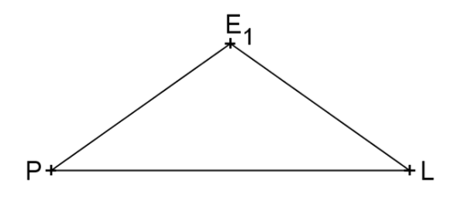
Die Punkte $P$ , $L$ und $E_1$ bilden die Eckpunkte eines gleichschenkligen Dreiecks (siehe Abbildung).
Konstruiere zwei weitere Punkte $E_2$ und $E_3$ so, dass auch die Dreiecke mit den Eckpunkten $P$ , $L$ und $E_2$ bzw. $P$ , $L$ und $E_3$ gleichschenklig sind und jeweils den gleichen Flächeninhalt wie das abgebildete Dreieck haben. Lote und Parallelen dürfen dabei mit dem Geodreieck gezeichnet werden.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichschenkliges Dreieck
Deine neuen Dreiecke sollen gleichschenklig sein, den gleichen Flächeninhalt wie das Dreieck $PLE_1$ haben und die Strecke $[PL]$ soll eine der Seiten sein.
Überlege dir nun als erstes, wann zwei Dreiecke mit gleicher Grundseite den gleichen Flächeninhalt haben: Den Flächeninhalt eines Dreiecks berechnet man, indem man Grundseite mit der Höhe und $\frac12$ mulipliziert. Wenn man die Länge der Grundseite gleich lässt (du nimmst hier genau die gleiche Grundseite) und man den gleichen Flächeninhalt erhalten will, muss man also auch die Höhe gleich lassen.
Zusätzlich willst du noch, dass die Dreiecke gleichschenklig sind. Welche Rollen kann dann die Strecke $[PL]$ erfüllen? Sie kann entweder die Seite sein, die es einmal gibt, dann müssen die anderen beiden Seiten gleich lang sein. Alternativ kann es die Seite sein, die es von der Länge doppelt gibt.
Die erste Möglichkeit ist die leichter sichtbare: Du willst also ein Dreieck mit $[PL]$ als Grundseite, der gleichen Höhe wie das ursprüngliche Dreieck und schließlich sollen die neuen beiden Seiten beide gleich lang sein. Das heißt, du musst das Dreieck und damit auch den Punkt $E_1$ an $[PL]$ spiegeln.
Dafür zeichnest du zwei Kreise mit den Mittelpunkten $P$ und $L$ jeweils durch den Punkt $E_1$ . Der zweite Schnittpunkt der beiden Kreise ist der Punkt $E_2$ . Diese Konstruktion kannst du auch in dem Applet nachvollziehen, ziehe dazu einfach den Schieberegler nach rechts.
Bei der anderen Variante brauchst du wieder ein Dreieck mit der Grundseite $[PL]$ , der Höhe des ursprünglichen Dreiecks und nur soll diesmal eine der anderen Seiten genau so lang sein wie $\overline{PL}$ .
Dafür zeichnest du dir als erstes eine Parallele zu $[PL]$ durch den Punkt $E_1$ . Damit stellst du sicher, dass das Dreieck die richtige Höhe haben wird. Anschließend zeichnest du mit dem Zirkel einen Kreis $L$ oder $P$ mit einem Radius von $\overline{PL}$ , um zu erreichen, dass es eine weitere Seite mit der Länge $\overline{PL}$ gibt. Der Punkt $E_3$ ist der Schnittpunkt zwischen der Gerade und dem Kreis.
6
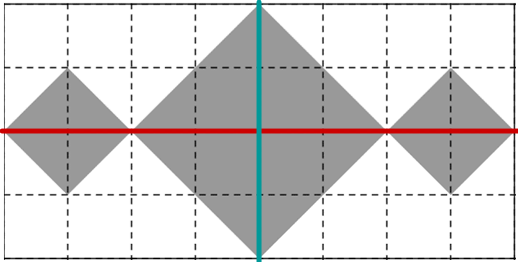
Das abgebildete Rechteck enthält eine Figur, die aus drei grau gefärbten Quadraten besteht. Alle Eckpunkte liegen auf Gitterpunkten.
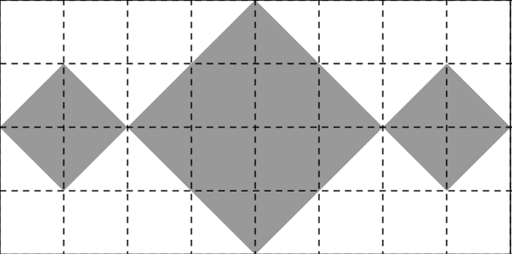
1. Gib den Anteil der Rechtecksfläche, der durch die Figur bedeckt wird, in Form eines Bruchs an. (1 BE)
  
  Wenn man sich die Kästchen anschaut, die von der Figur verdeckt werden, erkennt man, dass $4$ Kästchen ganz, und $16$ Kästchen nur halb verdeckt werden. Die $16$ halb verdeckten Kästchen ergeben zusammen $16\cdot \frac12=8$ ganze Kästchen.
  Das ergibt zusammen $4+8=12$ ganz verdeckte Kästchen.
  Du willst den Anteil berechnen:
  Der Anteil ist $\displaystyle\frac38$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Wie viele Symmetrieachsen besitzt die Figur? Kreuze an. (1 BE)
  keine
  genaue eine
  genau zwei
  genau vier
  genau sechs
  
  Die Figur besitzt genau $2$ Symmetrieachsen, einmal waagerecht (rote Linie) und einmal senkrecht (türkise Linie) durch die Mitte.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

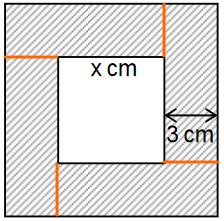
Zwei Quadrate liegen so ineinander, dass jede Seite des inneren Quadrats von der entsprechenden Seite des äußeren Quadrats den Abstand $3\ cm$ hat. Die Seiten der beiden Quadrate begrenzen eine Fläche mit dem Inhalt $360\ cm^2$ , die in der nicht maßstabsgetreuen Abbildung schraffiert dargestellt ist.

Jakob und Lukas sollen die Seitenlänge des inneren Quadrats bestimmen. Sie verwenden dazu unterschiedliche Ansätze:

Ansatz von Jakob: $(x+6)^2-x^2=360$

Ansatz von Lukas: $4\cdot[3\cdot(x+3)]=360$

Erkläre den Ansatz von Jakob in Worten. (1 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadrats
Um herauszufinden, was Jakob gedacht hat, überlegst du dir am besten zuerst, was die einzelnen Teile der Gleichung für eine Bedeutung haben.
$360$
Das ist die Größe des Flächeninhalts.
$x^2$
Das ist der Flächeninhalt des kleinen Quadrats, weil du für den Flächeninhalt eines Quadrats immer die Seitenlänge mit sich selbst multiplizieren musst.
$(x+6)^2$
Das ist der Flächeninhalt des großen Quadrats, da die Seitenlänge davon $x+3+3=x+6$ ist. Du addierst zu der Länge $x$ zweimal die kleinen Seitenstücke und für den Flächeninhalt quadrierst du dein Ergebnis.
Jakob hat $(x+6)^2-x^2=360$ gerechnet, wie du jetzt weißt entspricht das:
großes Quadrat - kleines Quadrat = Flächeninhalt der grauen Fläche
Jakob zieht also den Flächeninhalt des kleinen Quadrats von dem des großen Quadrats ab und erhält damit den grauen Flächeninhalt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
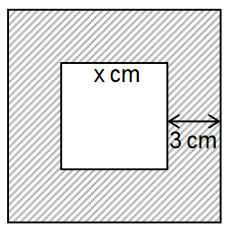
Veranschauliche den Ansatz von Lukas durch geeignete Eintragungen in die obige Abbildung. (1 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechtecks
Lukas Term ist $4\cdot [3\cdot (x+3)]$ . Es geht um die Berechnung des Flächeninhalts des grauen Gebildes. Er nimmt hier $4$ mal $[3\cdot(x+3)]$ . Also könntest du dir überlegen, ob es eine Möglichkeit gibt, die Fläche in vier gleich große Stücke zu zerteilen.
$3$ ist die kurze Seitenlänge eines Seitenstreifens.
$x+3$ ist die Seitenlänge des kleinen Quadrats und die Länge eines kleineren Seitenstreifens zusammen.
$3\cdot (x+3)$ entspricht damit dem Flächeninhalt eines Rechtecks mit diesen beiden Seiten, weil man dafür die Seitenlängen multipliziert.
Und $4\cdot [3\cdot (x+3)]$ entspricht dann $4$ solchen Rechtecken.
Deswegen zeichnest du wie in dem Bild, vier solche Rechtecke in die Abbildung.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Bestimme die Lösung der Gleichung $4\cdot[3\cdot(x+3)]=360$ über der Grundmenge $\mathbb{Q}$ . (2 BE)

8
Jährlich gelangen etwa 10 Millionen Tonnen Müll ins Meer, $80\ \%$ davon aus Plastik. Man kann davon ausgehen, dass $70\ \%$ dieses Plastikmülls auf den Meeresboden sinken, $15\ \%$ dauerhaft an der Wasseroberfläche schwimmen und $15\ \%$ an Strände gespült werden.
Seitenlänge des Rechtecks:
Länge: _km
Breite: _km
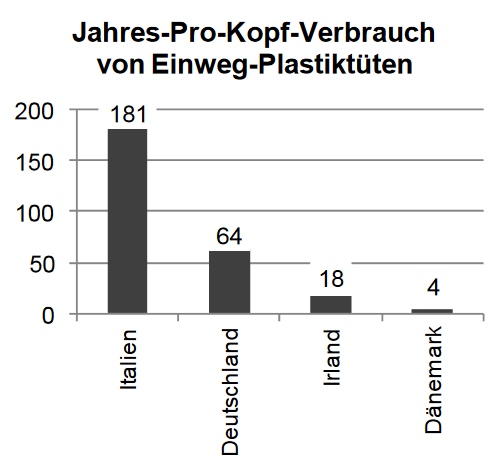
Der Jahres-Pro-Kopf-Verbrauch von Einweg-Plastiktüten wurde zuletzt 2010 erhoben und ist für vier Länder in der Grafik dargestellt.
1. Berechne, wie viele Tonnen des in einem Jahr ins Meer gelangten Plastikmülls demnach an Strände gespült werden. (2 BE)
  
  Rechne zuerst den Anteil von Plastikmüll am gesamten Müll (Prozentwert) aus, indem du die Grundmenge (gesamter Müll) mit dem Prozentsatz ( $80\ \%$ ) multiplizierst:
  $\def\arraystretch{1.25} \begin{array}{l}10\;000\;000\;\text{t}\cdot0{,}8=8\;000\;000\;\text{t}\end{array}$
  Da du wieder den Prozentwert berechnen willst (nur der Plastikmüll, der an die Strände gespült wird), musst du wieder Grundwert mit Prozentsatz multiplizieren. Hier ist der Grundwert nun der Plastikmüll, also das Ergebnis, das du gerade berechnet hast. Der Prozentsatz ist $15\%$ .
  Es werden demnach $1{,}2$ Mio $t$ Plastikmüll an den Strand gespült.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
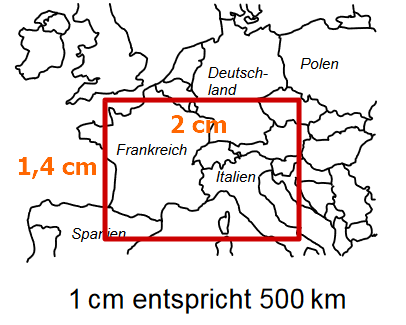
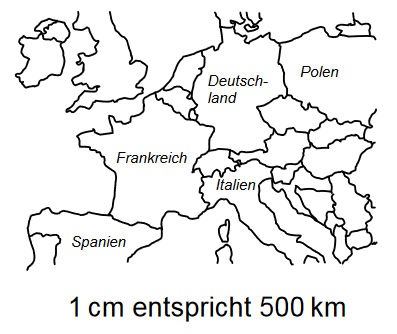
2. Der Great Pacific Garbage Patch im Nordpazifik ist ein Bereich, in dem besonders viel Müll schwimmt. Seine Größe wird auf mindestens $700\; 000\; km^2$ geschätzt. Veranschauliche diese Größe, indem du die Seitenlängen eines Rechtecks mit dem Flächeninhalt $700\; 000\; km^2$ angibst und dieses Rechteck maßstabsgetreu in die abgebildete Karte einzeichnest. (2 BE)
  
  Zuerst musst du dir mögliche Seitenlängen für ein Rechteck mit $700\;000\; km^2$ Fläche überlegen.
  Es kommen zum Beispiel $700\ km$ und $1000\ km$ in Frage, da sie zusammen eine Fläche von $700\cdot 1000=700\; 000$ ergeben.
  Als letztes rechnest du diese Länge noch in den Maßstab der Zeichnung um:
  $700:500=1{,}4\ cm$
  $1000:500=2{,}0\ cm$
  Also zeichnest du ein Rechteck mit den Seitenlängen $1{,}4\ cm$ und $2{,}0\ cm$ in die Zeichnung ein.
  Hinweis: Es gibt weitere Lösungsmöglichkeiten. Eine Lösung ist richtig, sobald ihr Produkt genau wie $1{,}4 ~cm\cdot 2~cm= 2{,}8\; cm^2$ ergibt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. In Irland war nach Einführung einer Abgabe auf den Vertrieb von Tüten der Jahres-Pro-Kopf-Verbrauch um $90\ \%$ auf den in der Grafik enthaltenen Wert gesunken. Gib den Jahres-Pro-Kopf-Verbrauch in Irland vor Einführung der Abgabe an. (1 BE)
  
  Berechnung über Dreisatz
  Da sich der Verbrauch um $90\ \%$ verringert hat, kann man auch sagen, dass von der ursprünglichen Anzahl nur noch $100\ \%-90\ \%=10\ \%$ übrig sind.
  Also entsprechen $10\ \%$ dem aktuellen Wert, $18$ Plastiktüten.
  Der Anteil vor der Abgabe war $100\ \%$ , also $10\cdot10\ \%$ . Deswegen musst du $10\cdot 18$ rechnen, um zu wissen, wie viele Plastiktüten vorher verbraucht wurden.
  $10\cdot 18=180$
  Vor der Einführung der Abgabe hat ein durchschnittlicher Irländer $180$ Plastiktüten pro Jahr verbraucht.
  Berechnung über die Prozentformel
  Stelle einen Ansatz auf, in dem $x$ die gesuchte Zahl an Plastiktüten ist. Da sich der Verbrauch um $90\ \%$ verringert hat, kann man auch sagen, dass von der ursprünglichen Anzahl nur noch $100\ \%-90\ \%=10\ \%$ übrig sind.
  Die gesuchte Zahl ist dann der Grundwert, die aktuelle Anzahl von Plastiktüten der Prozentwert und $10\ \%$ der Prozentsatz. Da man den Grundwert mit dem Prozentsatz multiplizieren muss, um den Prozentwert herauszubekommen, ergibt sich folgender Ansatz:
  Nun musst du noch nach $x$ auflösen, indem du durch $10\ \%=0{,}1$ (Prozent in Dezimalzahl umrechnen) teilst:
  Vor der Einführung der Abgabe hat ein durchschnittlicher Irländer $180$ Plastiktüten pro Jahr verbraucht.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Der Jahres-Pro-Kopf-Verbrauch für die Einwohner aller vier Länder zusammen kann nicht mit dem Ansatz $(181+64+18 +4 ) : 4$ berechnet werden. Gib an, welche zusätzlichen Informationen man für eine korrekte Berechnung benötigt. (1 BE)
  
  Den durchschnittlichen Jahres-Pro-Kopf-Verbrauch berechnest du, indem du "gesamter Verbrauch" geteilt durch "gesamte Einwohnerzahl" rechnest. Den gesamten Verbrauch erhältst du, wenn du die Durchschnittswerte der einzelnen Länder jeweils mit deren Einwohnerzahl multipliziert und anschließend addierst. Also müsstest du
  $181\cdot\text{Einwohnerzahl Italien}+64\cdot\text{Einwohnerzahl Deutschland}+\\18\cdot\text{Einwohnerzahl Irland}+4\cdot\text{Einwohnerzahl Dänemark}$
  berechnen.
  Man benötigt also die Einwohnerzahl der Länder.
  Bei dem gegebenen Ansatz würdest du nämlich nicht berücksichtigen, dass die Länder unterschiedlich viele Bewohner haben.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle 4\cdot[3\cdot(x+3)]$	$=$	$\displaystyle 360$
	↓	Multipliziere den Term in der eckigen Klammer aus.
$\displaystyle 4\cdot(3x+9)$	$=$	$\displaystyle 360$
	↓	Löse wieder durch Ausmultiplizieren die Klammern auf.
$\displaystyle 12x+36$	$=$	$\displaystyle 360$	$\displaystyle -36$
$\displaystyle 12x$	$=$	$\displaystyle 324$	$\displaystyle :12$
$\displaystyle x$	$=$	$\displaystyle 27$

Gruppe A

Teilaufgabe a)

Hast du eine Frage oder Feedback?

Teilaufgabe b)

Hast du eine Frage oder Feedback?

Sekunden ausrechnen

Meter pro Sekunde abschätzen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechnung über Dreisatz

Berechnung über die Prozentformel

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?