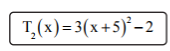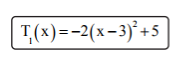Gegeben sind die beiden quadratischen Terme T1(x) und T2(x) Ordne den beiden Termen jeweils den passenden Extremwert mit der zugehörigenBelegung von x zu.
Wähle dazu zusammengehörige Kästchen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?