B I

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Im $\mathbb{R}^3$ sind der Punkt $P (2 \vert 6 \vert -8)$ , die Gerade $g: \vec{x}= \begin{pmatrix} -1 \\ 2 \\-3\end{pmatrix}+ \mu \cdot \begin{pmatrix} 2 \\ 2 \\ -3 \end{pmatrix}$ und die Ebenen $E_a: 2ax_1+ax_2-x_3 = 4a$ mit $a, \mu \in \mathbb{R}$ gegeben.
1. Geben Sie für $a=0$ die besondere Lage der Ebene $E_0$ im Koordinatensystem an. Der Punkt $P'$ ist der an $E_0$ gespiegelte Punkt $P$ . Geben Sie die Koordinaten des Spiegelpunktes $P'$ an. (3 BE)
  
  Einsetzen von a = 0
  $E_a: 2ax_1 + ax_2 - x_3 = 4a \\ E_0: 2\cdot0\cdot x_1 + 0\cdot x_2 - x_3 = 4 \cdot 0 \\ E_0: x_3 = 0$
  $\Rightarrow \$ Das entspricht der Gleichung der $x_1$ - $x_2$ -Ebene.
  Bestimmung der Koordinaten des Spiegelpunktes P'
  Der Punkt P' entsteht durch Spiegelung des Punktes $P$ an der $x_1$ - $x_2$ -Ebene.
  Dabei bleiben die $x_1$ und $x_2$ Koordinaten unverändert. Die $x_3$ Koordinate ändert ihr Vorzeichen.
  $P(2|6|-8) \ \ \Rightarrow \ \ P'(2|6|8)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze a = 0 in die Ebene $E_a$ ein.
  Besondere Lage $E_0$ bestimmen.
  Bestimme die Koordinaten des Spiegelpunktes P'.
2. Untersuchen Sie die gegenseitige Lage der Ebenen $E_a$ und der Geraden $g$ in Abhängigkeit von $a$ . (5 BE)
3. Die Ebene $F$ enthält den Punkt $P$ und die Gerade $g$ . Bestimmen Sie eine Koordinatengleichung von $F$ . (5 BE)
  $\left[ \text{Mögliches Ergebnis:} \;F:2x_1+x_2+2x_3=-6\right]$
4. Untersuchen Sie die gegenseitige Lage der Ebenen $E_a$ und $F$ in Abhängigkeit von $a$ . (5 BE)
5. Bestimmen Sie für $a = 1$ die Gleichung der Schnittgeraden $s$ der beiden Ebenen $E_1$ und $F$ . (4 BE)
6. Fertigen Sie eine aussagekräftige Skizze mit $E_1$ , $F$ , $g$ und $s$ an. Verwenden Sie dazu kein Koordinatensystem. (3 BE)
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die drei Zweigwerke $U$ , $V$ und $W$ eines Unternehmens sind nach dem Leontief-Modell miteinander und mit dem Markt wie im nebenstehenden Diagramm dargestellt verflochten. Alle Werte sind in Mengeneinheiten $ME$ angegeben, mit $a, b \in \mathbb{R}^+$
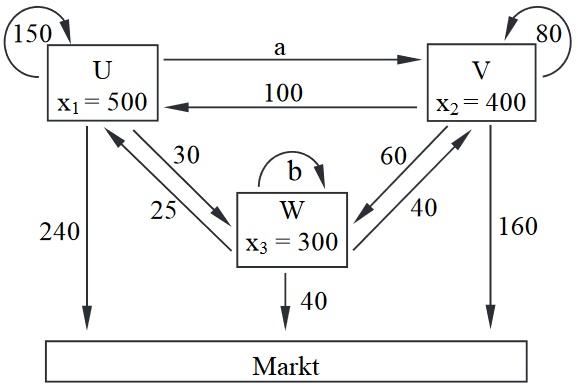
1. Bestimmen Sie $a$ , $b$ und die Inputmatrix $A$ . (4 BE)
2. Die Produktionskosten pro $ME$ betragen im Zweigwerk $U\ 75,-\ €$ , in $V\ 80,-\ €$ und in $W\ 95,-\ €$ . Der Erlös pro $ME$ auf dem Markt beträgt für die Produkte von Zweigwerk $U\ 215,-\ €$ , von $V\ 240,-\ €$ und von $W\ 170,-\ €$ . Berechnen Sie den Gesamtgewinn $G$ und erläutern Sie, wie die Geschäftsleitung auf dieses Ergebnis reagieren könnte. (Hinweis: Gesamtgewinn = Gesamterlös – Gesamtkosten) (4 BE)
3. Aufgrund einer technologischen Umstellung soll das Zweigwerk $V$ genau $600\ ME$ und $U$ höchstens $580\ ME$ produzieren. Untersuchen Sie, ob die Produktionen der Zweigwerke $U$ und $W$ so festgelegt werden können, dass dann alle drei Werke gleich viel an den Markt abgeben. (7 BE)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

B I

Einsetzen von a = 0

Bestimmung der Koordinaten des Spiegelpunktes P'

Hast du eine Frage oder Feedback?