Aufgaben zum Newtonschen Näherungsverfahren

1
Berechne mit Hilfe des Newtonsches Näherungsverfahren die Nullstellen folgender Funktionen auf zwei Nachkommastellen genau.
1. $f (x) = x^{3} - 5 x^{2} - 4 x + 2 f(x)=x³-5x²-4x+2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Newton-Verfahren
  Wertetabelle
  $f (x) = x^{3} - 5 x^{2} - 4 x + 2$
  Erstelle eine Wertetabelle um die Lage der Nullstellen einschränken zu können.
  x
  -3
  -2
  -1
  0
  1
  2
  3
  4
  5
  6
  f(x)
  -58
  -18
  0
  2
  -6
  -18
  -28
  -30
  -18
  14
  Bestimmen der Intervalle
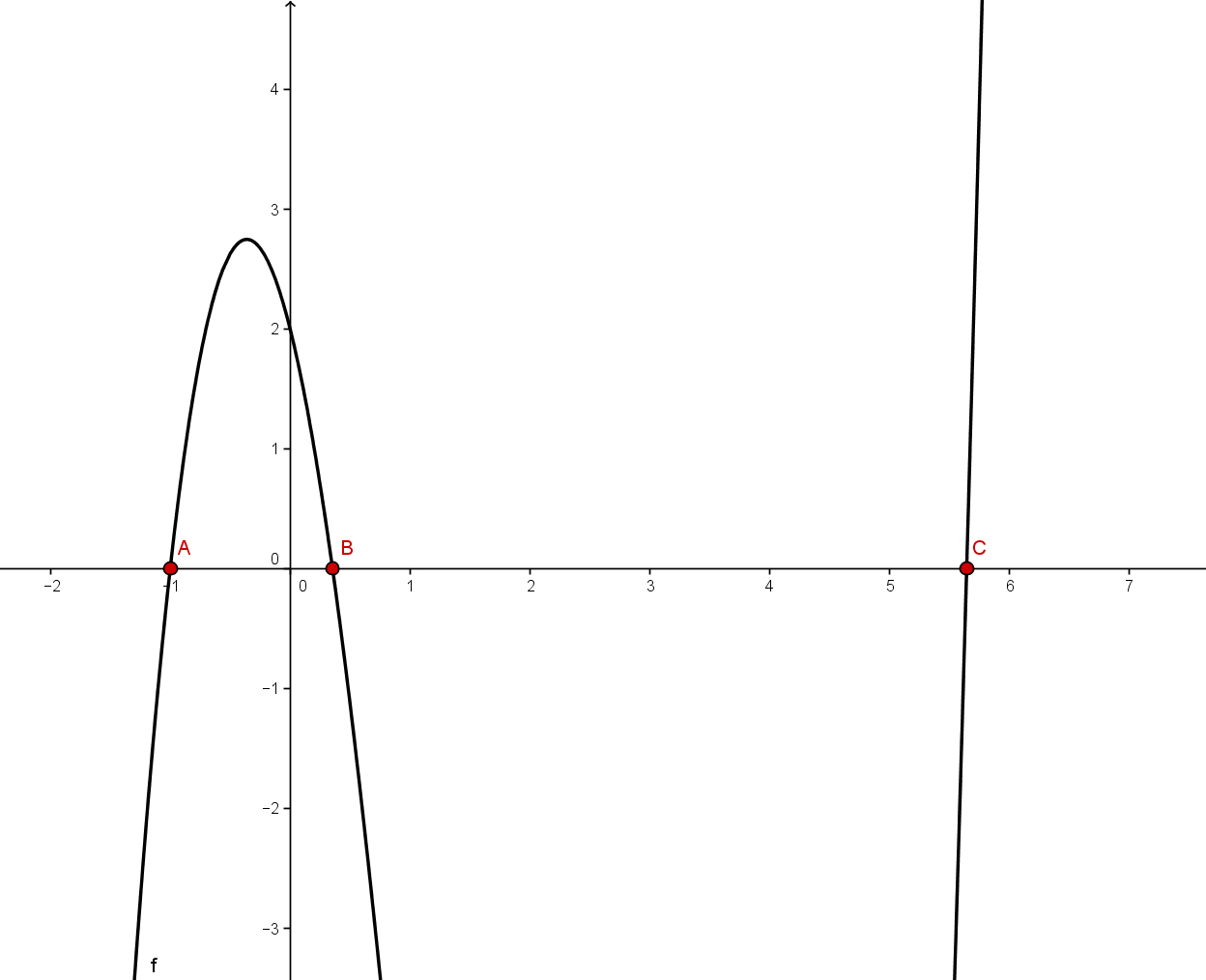
  Eine Nullstelle kann direkt aus der Tabelle abgelesen werden:
  $\tilde x_1=-1$
  Man sieht außerdem, dass die Funktion $f (x)$ in den Intervallen $] 0; 1 [$ und $] 5; 6 [$ ihr Vorzeichen ändert.
  Daraus folgt für die Nullstellen $\tilde x_{2{,}3}:$
  $\Rightarrow \tilde x_2\in \;]0;1[$ und $\tilde x_3\in\;]5;6[$
  Um die Intervalle weiter zu verkleinern und so einen besseren Anfangswert für das Newton-Verfahren zu bekommen, berechnet man den Funktionswert der Mittelwerte der ausgewählten Intervalle:
  x
  0
  0,5
  1
  5
  5,5
  6
  f(x)
  2
  -1,125
  -6
  -18
  -4,875
  14
  Man sieht nun, dass die Funktion $f (x)$ in den Intervallen $] 0; 0,5 [$ und $] 5,5; 6 [$ ihr Vorzeichen ändert.
  Daraus folgt für die Nullstellen $\tilde x_{2{,}3}:$
  $\Rightarrow \tilde x_2\in \;]0;0{,}5[$ und $\tilde x_3\in\;]5{,}5;6[$
  Anwenden des Newton-Verfahrens
  $f (x) = x^{3} - 5 x^{2} - 4 x + 2$
  $f^\prime(x)=3x^2-10x-4$
  $\displaystyle \Rightarrow x_{n+1}=x_n-\frac{x_n^3-5x_n^2-4x_n+2}{3x_n^2-10x_n-4}$
  Bestimmen der Nullstellen
  Man wählt einen beliebigen Wert $x_{0}$ aus dem Intervall $] 0; 0,5 [$ , z.B. $x_0=0{,}25$ .
  $\displaystyle x_1=x_0-\frac{x_0^3-5x_0^2-4x_0+2}{3x_0^2-10x_0-4}$
  Man berechnet jetzt $x_{1}$ mit der oben angegebenen Rekursionsformel.
  $\displaystyle =0{,}25-\frac{(0{,}25)^3-5\cdot(0{,}25)^2-4\cdot(0{,}25)+2}{3\cdot(0{,}25)^2-10\cdot(0{,}25)-4}$
  $\displaystyle =\frac{73}{202}\approx0{,}36139$
  $\displaystyle x_2=x_1-\frac{x_1^3-5x_1^2-4x_1+2}{3x_1^2-10x_1-4}$
  Dann berechnet man $x_{2}$ mit dem gerade berechneten $x_{1}$ und der oben angegebenen Rekursionsformel.
  $\displaystyle =\frac{73}{202}-\frac{(\frac{73}{202})^3-5\cdot(\frac{73}{202})^2-4\cdot(\frac{73}{202})+2}{3\cdot(\frac{73}{202})^2-10\cdot(\frac{73}{202})-4}$
  $\displaystyle =0{,}354276361\approx0{,}35428$
  $\displaystyle x_3=x_2-\frac{x_2^3-5x_2^2-4x_2+2}{3x_2^2-10x_2-4}$
  Dann berechnet man $x_{3}$ mit dem gerade berechneten $x_{2}$ und der oben angegebenen Rekursionsformel.
  $\displaystyle =0{,}354276361-\frac{(0{,}354276361)^3-5\cdot(0{,}354276361)^2-4\cdot(0{,}354276361)+2}{3\cdot(0{,}354276361)^2-10\cdot(0{,}354276361)-4}$
  $\displaystyle =0{,}3542486894\approx0{,}35425$
  Man erkennt jetzt, dass sich die Genauigkeit der Lösung im letzten Schritt nurnoch in der fünften Nachkommastelle verbessert.
  Da nur eine Angabe bis auf zwei Nachkommastellen gefordert war, ist man in diesem Schritt fertig und das Ergebnis lautet:
  $\displaystyle \tilde x_2=0{,}35$
  Um $\tilde x_3$ zu bestimmen verfährt man analog und erhält für den Startwert $x_0=5{,}75$ folgende Werte:
  $i$
  0
  1
  2
  3
  $x_{i}$
  $5,75$
  $5,649253731$
  $5,645755468$
  $5,645751311$
  Und somit erhält man:
  $\displaystyle \tilde x_3=5{,}65$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f(x)=\ln(x^4+5x³-5)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Newton-Verfahren
  $f(x)=\ln(x^4+5x^3-5)$
  Der natürliche Logarithmus $\ln(x)$ ist nur auf den positiven, reellen Zahlen definiert.
  Um die Nullstellen der Funktion $f (x)$ zu bestimmen macht man zuvor eine kurze Vorüberlegung.
  Man betrachtet die Nullstellen des natürlichen Logarithmus und stellt folgendes fest:
  Sei $g(x)=\ln(x)$ :
  $g(x)=0 \Leftrightarrow \ln(x)=0 \qquad \qquad \qquad\vert\ e$
  $e^{\ln(x)}=e^0 \qquad \qquad \qquad \qquad \qquad \quad$ Umformen.
  $\Rightarrow x=1$
  Man sieht, dass $x = 1$ die einzige Nullstelle von $\ln(x)$ ist.
  Um die Nullstellen von $f (x)$ zu approximieren, kann man also die "Einsstellen" der Funktion $h (x) = x^{4} + 5 x^{3} - 5$ approximieren, d.h. man sucht die Lösung für die Gleichung $h (x) = x^{4} + 5 x^{3} - 5 = 1$ .
  Da das Newtonverfahren Nullstellen approximiert macht man eine kleine Umformung und erhält:
  $h(x)=x^4+5x^3-5=1 \qquad \qquad \vert -1$
  $x^{4} + 5 x^{3} - 6 = 0$
  Wir approximieren also die Nullstellen der Funktion $\tilde h(x)=x^4+5x^3-6$ um die Nullstellen von $f (x)$ zu finden.
  Wertetabelle
  $x$
  -6
  -5
  -4
  -3
  -2
  -1
  0
  1
  2
  $\tilde h(x)$
  210
  -6
  -70
  -60
  -30
  -10
  -6
  0
  50
  Bestimmen der Intervalle
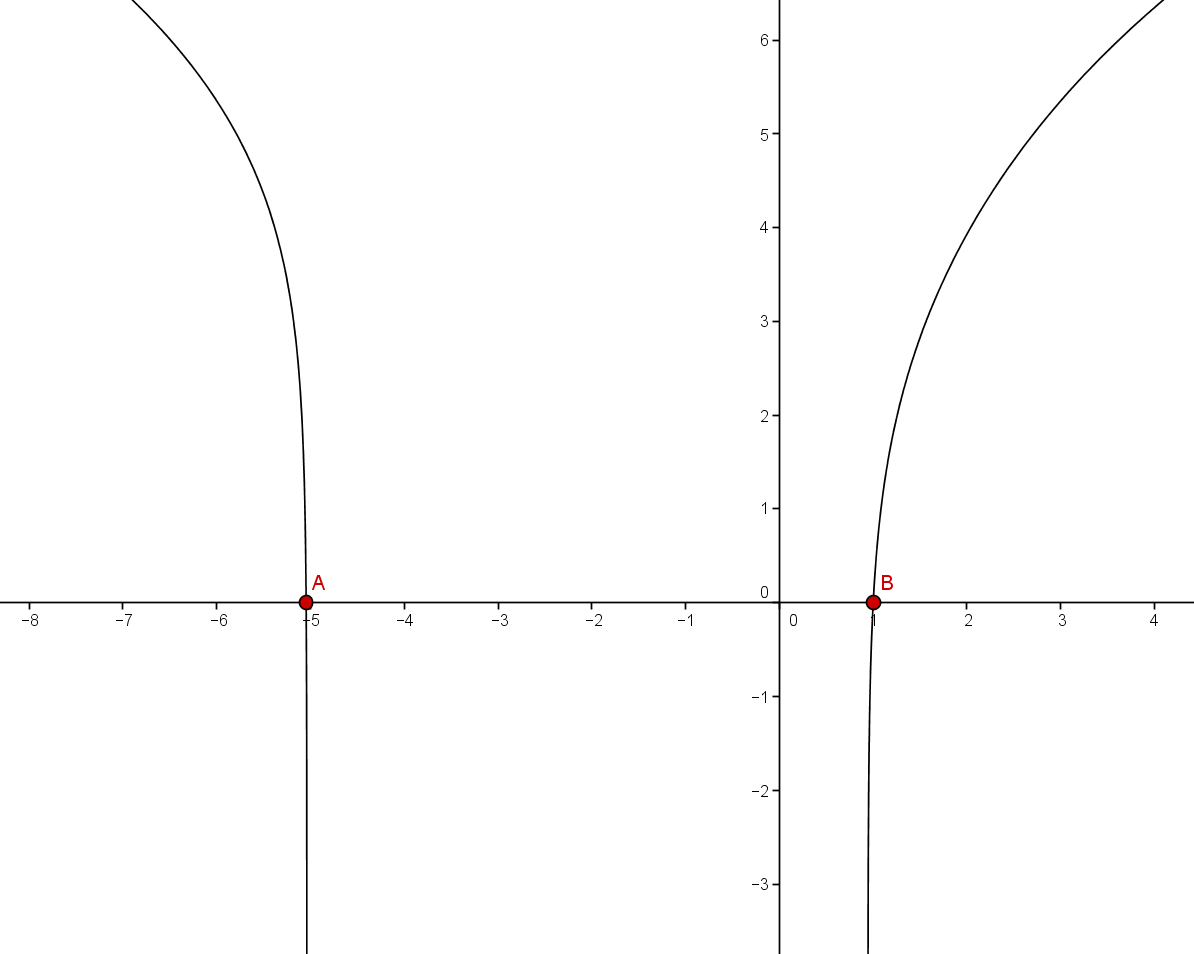
  Eine Nullstelle kann direkt aus der Tabelle abgelesen werden:
  $\tilde x_1=1$
  Man sieht außerdem, dass die Funktion $\tilde h(x)$ im Intervallen $] - 6; - 5 [$ ihr Vorzeichen ändert.
  Daraus folgt für die Nullstellen $\tilde x_{2}:$
  $\Rightarrow \tilde x_2\in \;]-6;-5[$
  Um das Intervall weiter zu verkleinern und so einen besseren Anfangswert für das Newton-Verfahren zu bekommen, berechnet man den Funktionswert der Mittelwerte der ausgewählten Intervalle:
  x
  -6
  -5,5
  -5
  f(x)
  210
  77,1875
  -6
  Man sieht nun, dass die Funktion $\tilde h(x)$ in den Intervallen $] - 5,5; - 5 [$ ihr Vorzeichen ändert.
  Daraus folgt für die Nullstellen $\tilde x_{2}:$
  $\Rightarrow \tilde x_2\in \;]-5{,}5;-5[$
  Anwenden des Newton-Verfahrens
  $\tilde h(x)=x^4+5x^3-6$
  $\tilde{h}^\prime(x)=4x^3+15x^2$
  $\displaystyle \Rightarrow x_{n+1}=x_n-\frac{x_n^4+5x_n^3-6}{4x_n^3+15x_n^2}$
  Bestimmen der Nullstellen
  Man wählt einen beliebigen Wert $x_{0}$ aus dem Intervall $] - 5,5; - 5 [$ , z.B. $x_0=-5{,}25$ .
  $\displaystyle \Rightarrow x_{1}=x_0-\frac{x_0^4+5x_0^3-6}{4x_0^3+15x_0^2}$
  Man berechnet jetzt $x_{1}$ mit der oben angegebenen Rekursionsformel.
  $\displaystyle =(-5{,}25)-\frac{(-5{,}25)^4+5(-5{,}25)^3-6}{4(-5{,}25)^3+15(-5{,}25)^2}$
  $=-5{,}067531179\approx-5{,}06753$
  $\displaystyle x_{2}=x_1-\frac{x_1^4+5x_1^3-6}{4x_1^3+15x_1^2}$
  Dann berechnet man $x_{2}$ mit dem gerade berechneten $x_{1}$ und der oben angegebenen Rekursionsformel.
  $\displaystyle =(-5{,}067531179)-\frac{(-5{,}067531179)^4+5(-5{,}067531179)^3-6}{4(-5{,}067531179)^3+15(-5{,}067531179)^2}$
  $=-5{,}046930085\approx-5{,}04693$
  $\displaystyle x_{3}=x_2-\frac{x_2^4+5x_2^3-6}{4x_2^3+15x_2^2}$
  Dann berechnet man $x_{3}$ mit dem gerade berechneten $x_{2}$ und der oben angegebenen Rekursionsformel.
  $\displaystyle =(-5{,}046930085)-\frac{(-5{,}046930085)^4+5(-5{,}046930085)^3-6}{4(-5{,}046930085)^3+15(-5{,}046930085)^2}$
  $=-5{,}046680361\approx-5{,}04668$
  Man erkennt jetzt, dass sich die Genauigkeit der Lösung im letzten Schritt nur noch in der vierten Nachkommastelle verbessert.
  Da nur eine Angabe bis auf zwei Nachkommastellen gefordert war, ist man in diesem Schritt fertig und das Ergebnis lautet:
  $\displaystyle \tilde x_2=-5{,}05$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

x	-3	-2	-1	0	1	2	3	4	5	6
f(x)	-58	-18	0	2	-6	-18	-28	-30	-18	14

x	0	0,5	1	5	5,5	6
f(x)	2	-1,125	-6	-18	-4,875	14

$i$	0	1	2	3
$x_{i}$	$5,75$	$5,649253731$	$5,645755468$	$5,645751311$

$x$	-6	-5	-4	-3	-2	-1	0	1	2
$\tilde h(x)$	210	-6	-70	-60	-30	-10	-6	0	50

x	-6	-5,5	-5
f(x)	210	77,1875	-6

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zum Newtonschen Näherungsverfahren

Wertetabelle

Bestimmen der Intervalle

Anwenden des Newton-Verfahrens

Bestimmen der Nullstellen

Hast du eine Frage oder Feedback?

Wertetabelle

Bestimmen der Intervalle

Anwenden des Newton-Verfahrens

Bestimmen der Nullstellen

Hast du eine Frage oder Feedback?