Die Zufallsgröße X kann die Werte 0, 1, 2 und 3 annehmen. Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von X mit .
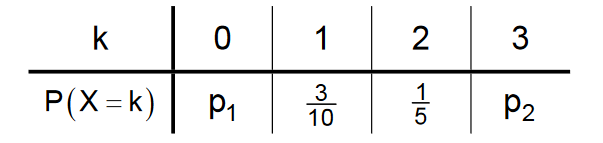
Zeigen Sie, dass der Erwartungswert von X nicht größer als 2,2 sein kann. (3 BE)
Die Zufallsgröße X kann die Werte 0, 1, 2 und 3 annehmen. Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von X mit .
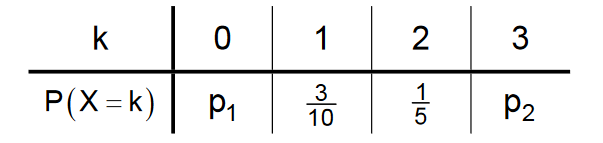
Zeigen Sie, dass der Erwartungswert von X nicht größer als 2,2 sein kann. (3 BE)