Aufgaben zum Venn-Diagramm
- 1
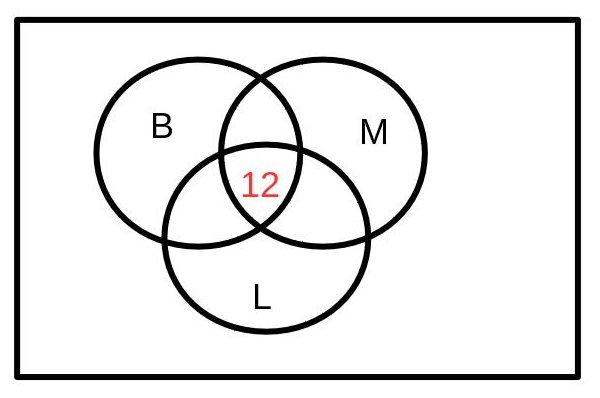
Von 200 Autos, die überprüft wurden haben 78 Mängel an den Bremsen, 72 Mängel an dem Motor und 56 Mängel an der Lichtanlage. Genau 20 Fahrzeuge hatten Probleme an Bremsen und Motor, 19 hatten Mängel an Motor und Lichtanlage und 26 Fahrzeuge an Bremsen und der Lichtanlage. 12 Autos hatten Probleme in allen drei untersuchten Bereichen. Wie viele Fahrzeuge hatten keine Mängel?
- 2
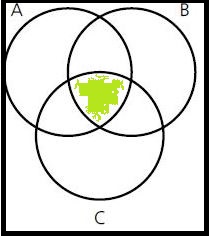
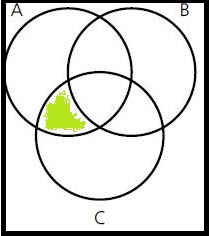
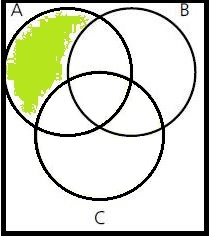
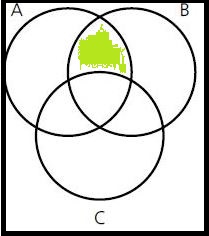
Schraffiere die gegebene Menge in einem Venn-Diagramm!
- 3
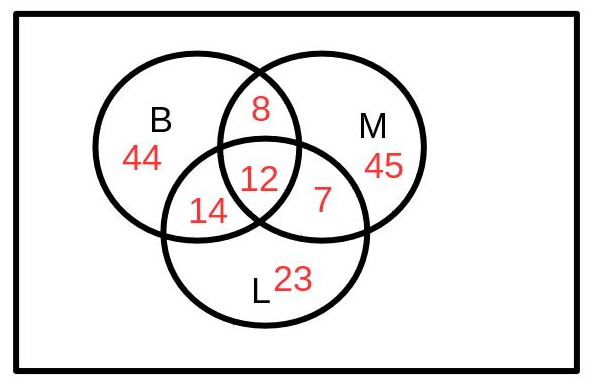
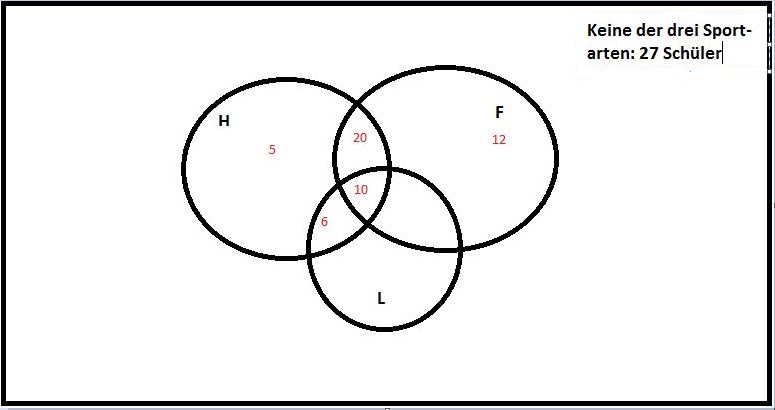
Unter 100 Schülern wird eine Umfrage bezüglich ihrer Lieblingssportart gemacht, wobei nur nach Handball, Fußball und Leichtathletik gefragt wird.
12 Schüler spielen gerne Fussball, sind aber weder für Handball noch für Leichtathletik zu begeistern. 5 Schüler spielen gerne Handball, aber nicht Fußball und mögen auch nicht Leichtathletik. 30 Schüler spielen gerne zwei von den Sportarten, wobei darunter 20 sind die gerne Fußball und Handball spielen und 6 Schüler die gerne Handball spielen und Leichtathletik mögen. Genau 10 Schüler mögen alle drei Sportarten gleich gern. 27 Schüler betreiben am liebsten gar keinen Sport.
Wieviel Schüler mögen gerne Leichtathletik, aber spielen weder Handball noch Fußball gern?
Wie viele Schüler mögen Leichtathletik nicht?
Wie viele Schüler, die gerne Fußball spielen, spielen nicht gerne Handball?
Löse die Aufgabe mit Hilfe eines Venn-Diagramms!
- 4
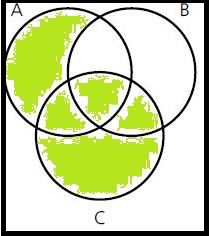
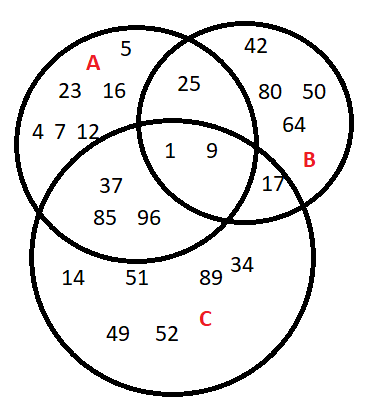
Beurteile anhand des Diagramms ob die folgenden Aussagen wahr oder falsch sind!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?