Kurvendiskussion
- 1
Gib den Term einer (möglichst einfachen) gebrochen rationalen Funktion f an, die folgende Eigenschaften besitzt.
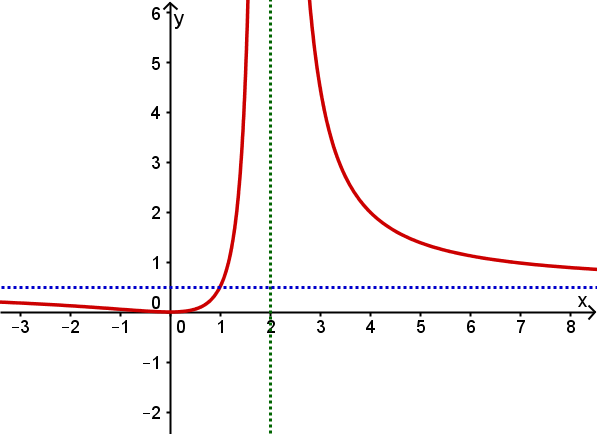
Der Graph von berührt die x-Achse an der Stelle ;
die Funktion hat die Polstelle .
Der Graph von f hat eine Polstelle ohne Vorzeichenwechsel bei und für die Asymptote
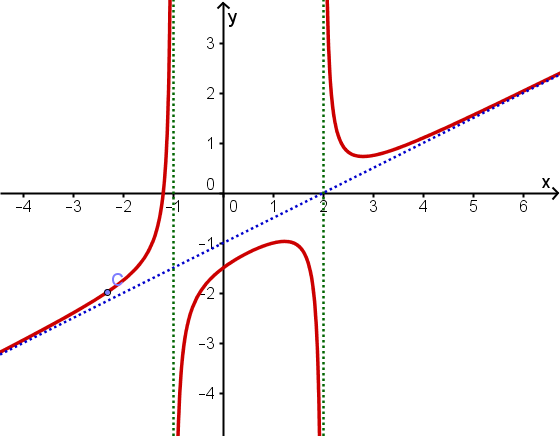
Der Graph von f hat Polstellen mit Vorzeichenwechsel bei und und für die Asymptote
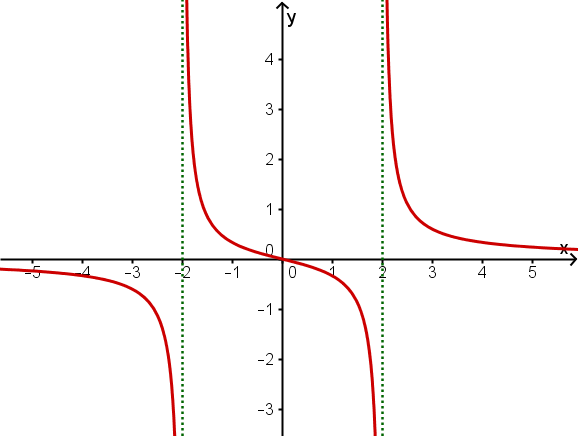
Der Graph von f hat eine Polstelle mit Vorzeichenwechsel bei , ist punktsymmetrisch zum Ursprung und hat für die Asymptote
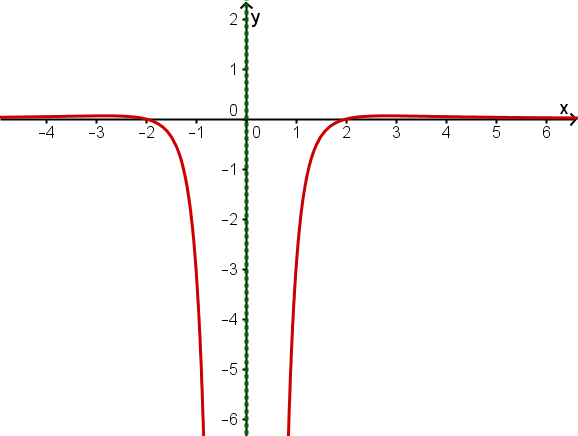
Der Graph von f hat eine Polstelle bei und ist achsensymmetrisch zur y-Achse.
Für hat der Graph die Asymptote und bei befindet sich eine Nullstelle.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?