Wie groß ist die Innenwinkelsumme der folgenden Formen:
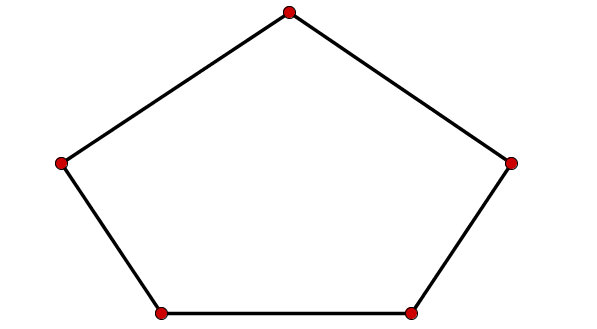
Für diese Aufgabe benötigst Du folgendes Grundwissen: Innenwinkelsumme
Die Innenwinkelsumme kann man entweder mit der Formel berechnen oder über die Zerlegung des n-Ecks in Dreiecke bestimmen.
Einerseits kann man die Innenwinkel Summe durch die Formel errechnen. Also in dem Fall
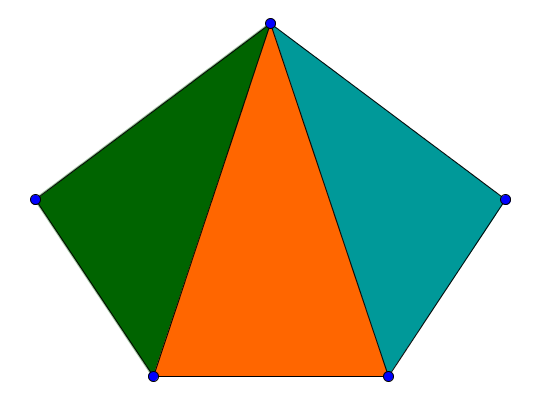
Die zweite Möglichkeit ist, dass man das n-Eck in Dreiecke unterteilt. Die Dreiecke müssen dabe ihre Ecken in den Ecken des n-Ecks haben. Da ein Dreieck die Innenwinkelsumme hat, kann man die Innenwinkelsumme folgendermaßen betiimen:
Anzahl der Dreicke
Hier lässt sich das 5-Eck in solche Dreiecke zerteilen, also gilt:
Hast du eine Frage oder Feedback?
Informiere dich über die Merkmale eines Dreiecks, Vierecks und Fünfecks! Behalte das als Grundwissen.
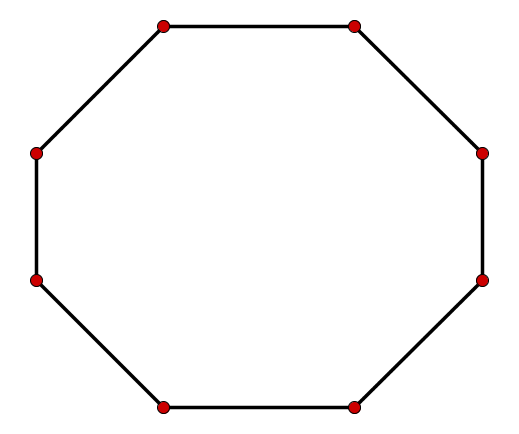
Für diese Aufgabe benötigst Du folgendes Grundwissen: Innenwinkelsumme
Unterteile das Achteck in gleich große Dreiecke. Die Dreiecke müssen dabe ihre Ecken in den Ecken des n-Ecks haben. Da ein Dreieck die Innenwinkelsumme hat, kann man die Innenwinkelsumme folgendermaßen bestimmen:
Anzahl der Dreicke
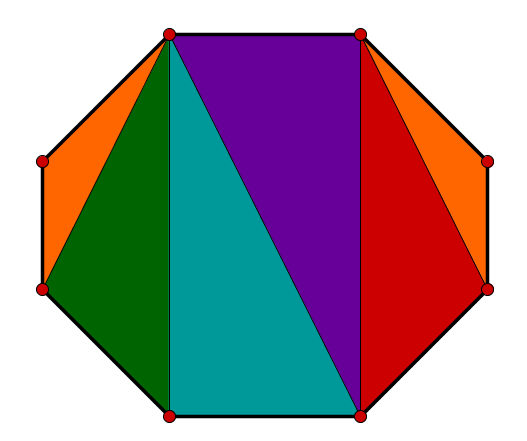
Hier lässt sich das 8-Eck in solche Dreiecke zerteilen, also gilt:
Hast du eine Frage oder Feedback?
Hier kannst du das Achteck in gleich große Dreiecke zerlegen und so auf das Resultat der Innenwinkel kommen!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkelsumme
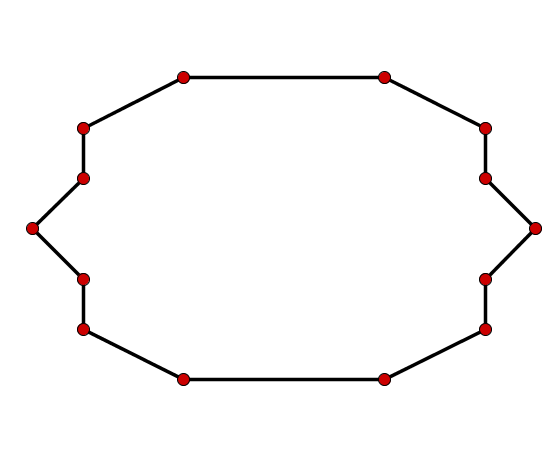
Einerseits kann man die Innenwinkelsumme eines n-Ecks mit der Formel berechnen. Also in diesem Fall mit (14 - 2) x 180 = 2160.
Die zweite Möglichkeit ist, dass man das n-Eck in Dreiecke unterteilt. Die Dreiecke müssen dabe ihre Ecken in den Ecken des n-Ecks haben. Da ein Dreieck die Innenwinkelsumme hat, kann man die Innenwinkelsumme folgendermaßen betiimen:
Anzahl der Dreicke
Hier lässt sich das 14-Eck in solche Dreiecke zerteilen, also gilt:
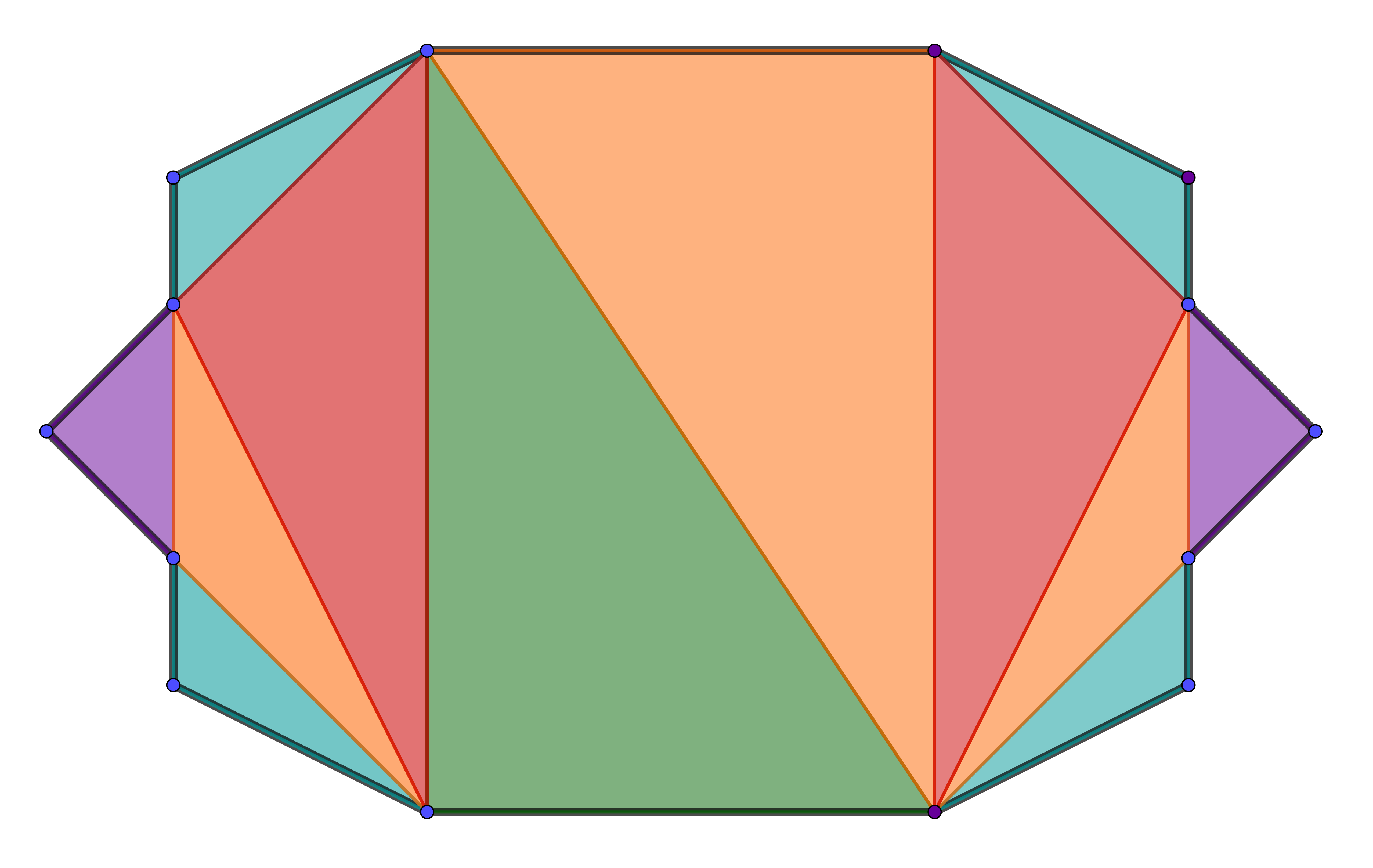
Hast du eine Frage oder Feedback?
Die Winkelsumme (siehe Grundwissen!) eines n-Ecks kann man entweder mit der Formel berechnen oder sich durch Unterteilung in Dreicke herleiten.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
