Aufgaben zur direkten Proportionalität
- 1
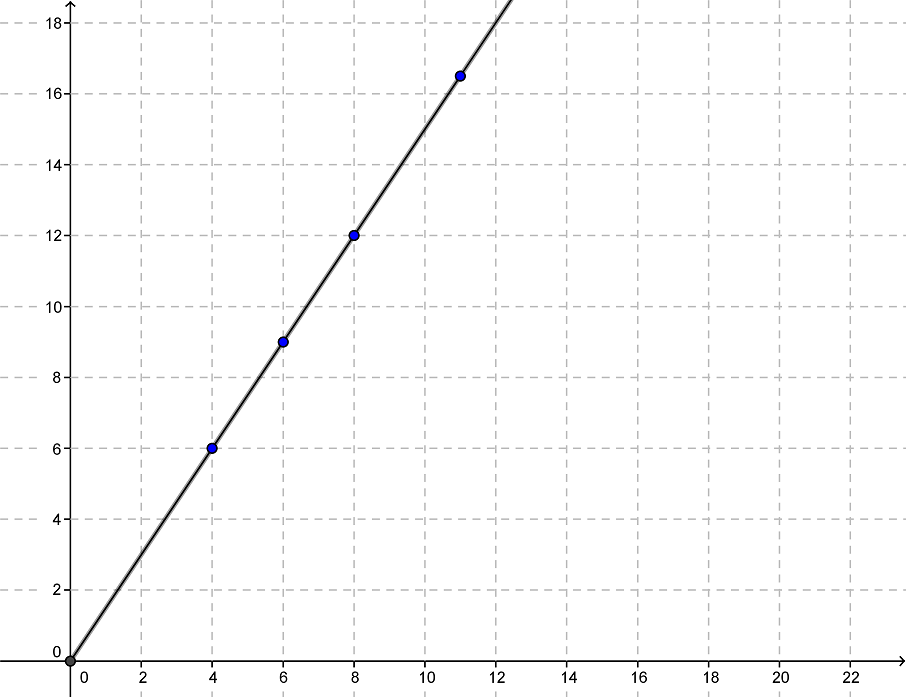
Die folgende Wertetabelle enthält direktproportionale Wertepaare. Berechne die fehlenden Werte und trage die Wertepaare in ein Gitternetz ein.
Menge in Liter
4
6
8
Preis in €
6
12
16,5
- 2
Ein 8,4m langer Pfahl steckt zu im Boden und zu 30% im Wasser. Fertige eine Skizze mit den gegebenen Daten an und berechne, wie viele Meter des Pfahls aus dem Wasser herausragen.
m - 3
Ein Getränkemarkt verkauft für ein Fest 55 Kisten Cola für 522,50 Euro. Wie viel muss man für 77 Kisten zahlen, wenn es keinen Rabatt gibt?
€ - 4
Ein Getränkemarkt verkauft für ein Fest 55 Kisten Cola für 522,50 Euro. Wie viele Kisten erhält man für 200 Euro? (Aufschreiben des Rechenausdrucks genügt, ausrechnen ist nicht verlangt.)
Kisten erhält man ungefähr für 200€. - 5
Überprüfe, ob jeweils eine direkte proportionale Zuordnung vorliegt und begründe kurz.
Verbrauch in l
Strecke in km
4,25
70
12,75
210
Stückzahl
Preis in €
2
1,60
4
3,20
10
7,20
Menge in kg
Preis in €
2,5
10
0,5
2,5
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?