Aus einem Zylinder mit dem Radius und der Körperhöhe wird ein Viertel herausgeschnitten.Berechne die gesamte Oberfläche des entstandenen Körpers. (4 Punkte)
Hinweis: Skizze nicht maßstabgetreu
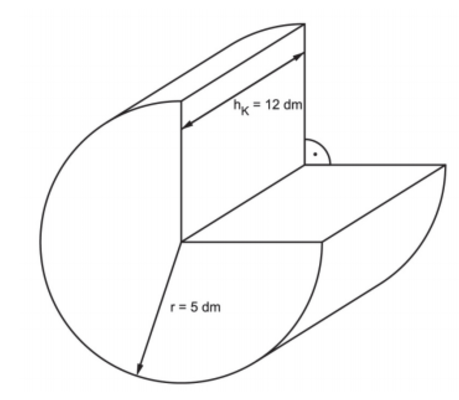
Aus einem Zylinder mit dem Radius und der Körperhöhe wird ein Viertel herausgeschnitten.Berechne die gesamte Oberfläche des entstandenen Körpers. (4 Punkte)
Hinweis: Skizze nicht maßstabgetreu
