Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadrat
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von
YouTube geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer
Datenschutzerklärung .
[https://youtu.be/_oPbMylE11A]
Bestimmung des Flächeninhalts und Umfangs eines Quadrates. Gegeben:
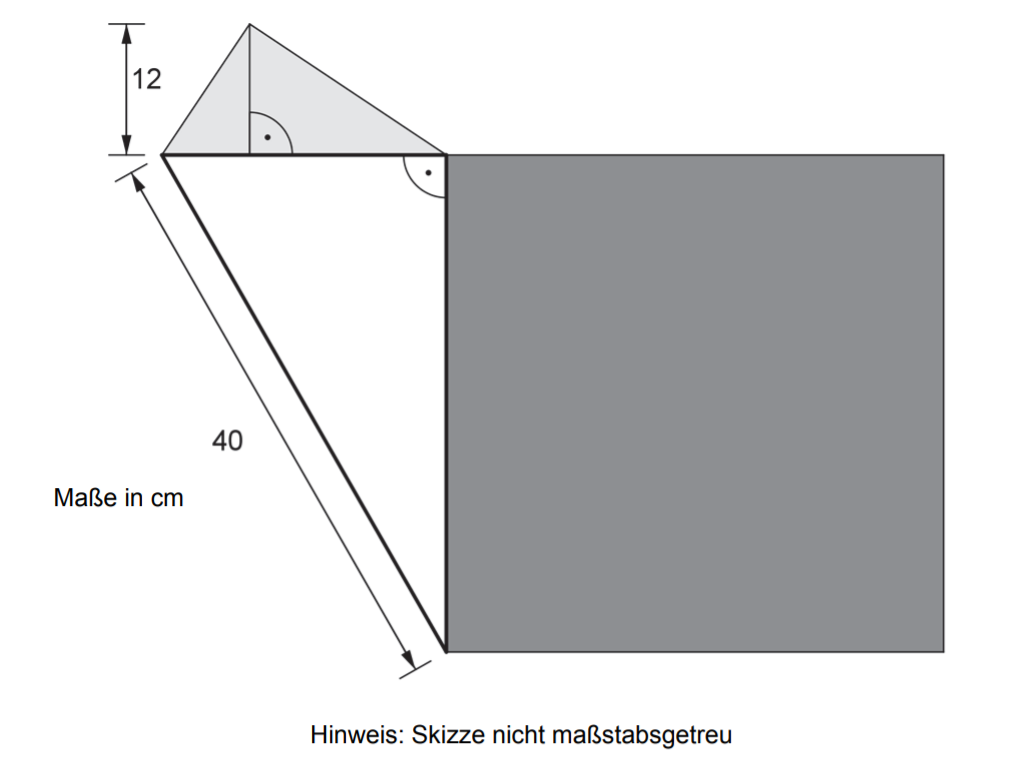
Flächeninhalt des hellgrauen Dreiecks: A D r e i e c k = 144 [ c m 2 ]
Aus der Skizze: Höhe des hellgrauen Dreiecks h = 12 [ c m ]
Aus der Skizze: Seitenlänge eines der Seiten des weißen Dreiecks b = 40 [ c m ]
Gesucht: Flächeninhalt und Umfang des dunkelgrauen Quadrats
Vorüberlegung Um den Flächeninhalt und den Umfang des Quadrats zu berechnen, musst du zunächst die Seitenlänge a
Um a b g
g
Die Grundseite g des hellgrauen Dreiecks bestimmen Berechne g A D r e i e c k h
Die Formel für den Flächeninhalt lautet:
⇒ g = 2 ⋅ A D r e i e c k h = 2 ⋅ 144 c m 2 12 c m = 2 ⋅ 12 ⋅ 12 c m 2 12 c m
(Alternativ kannst du auch A = 144 und h = 12 sofort einsetzen und dann g berechnen. Das geht etwas einfacher.)
Die Seite a des Quadrats bestimmen Um a b g a Satzes des Pythagoras berechnen (siehe obige Skizze):
Nun setze die Längen für b und g
( 40 c m ) 2 = a 2 + ( 24 c m ) 2 − ( 24 c m ) 2
(Das ist bereits der Flächeninhalt des Quadrats. Er wird unten nur zur Sicherheit noch einmal ausführlich berechnet.)
Da a
Den Flächeninhalt des Quadrats bestimmen A Q u a d r a t = a ⋅ a = 32 c m ⋅ 32 c m = 1024 c m 2
Den Umfang des Quadrats bestimmen U Q u a d r a t = a + a + a + a = 4 ⋅ a = 4 ⋅ 32 c m = 128 c m