Nachtermin Teil A - lernen mit Serlo!

Dieser Inhalt wurde gelöscht.

Punkte zu Aufgabe 3.1: 2 P

Punkte zu Aufgabe 3.2: 3 P

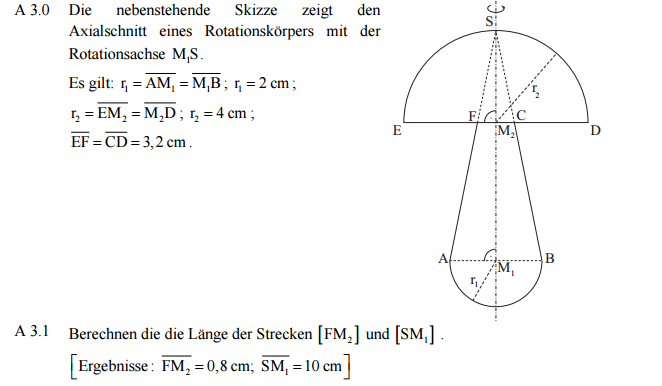
Lösung zur Teilaufgabe A 3.1

In dieser Teilaufgabe geht es darum, die Länge der Strecke $[F M_{2}]$ und $[S M_{1}]$ zu bestimmen.

Länge der Strecke $[F M_{2}]$

Die Länge der Strecke $[F M_{2}]$ bestimmen wir durch Subtraktion zweier Längen.

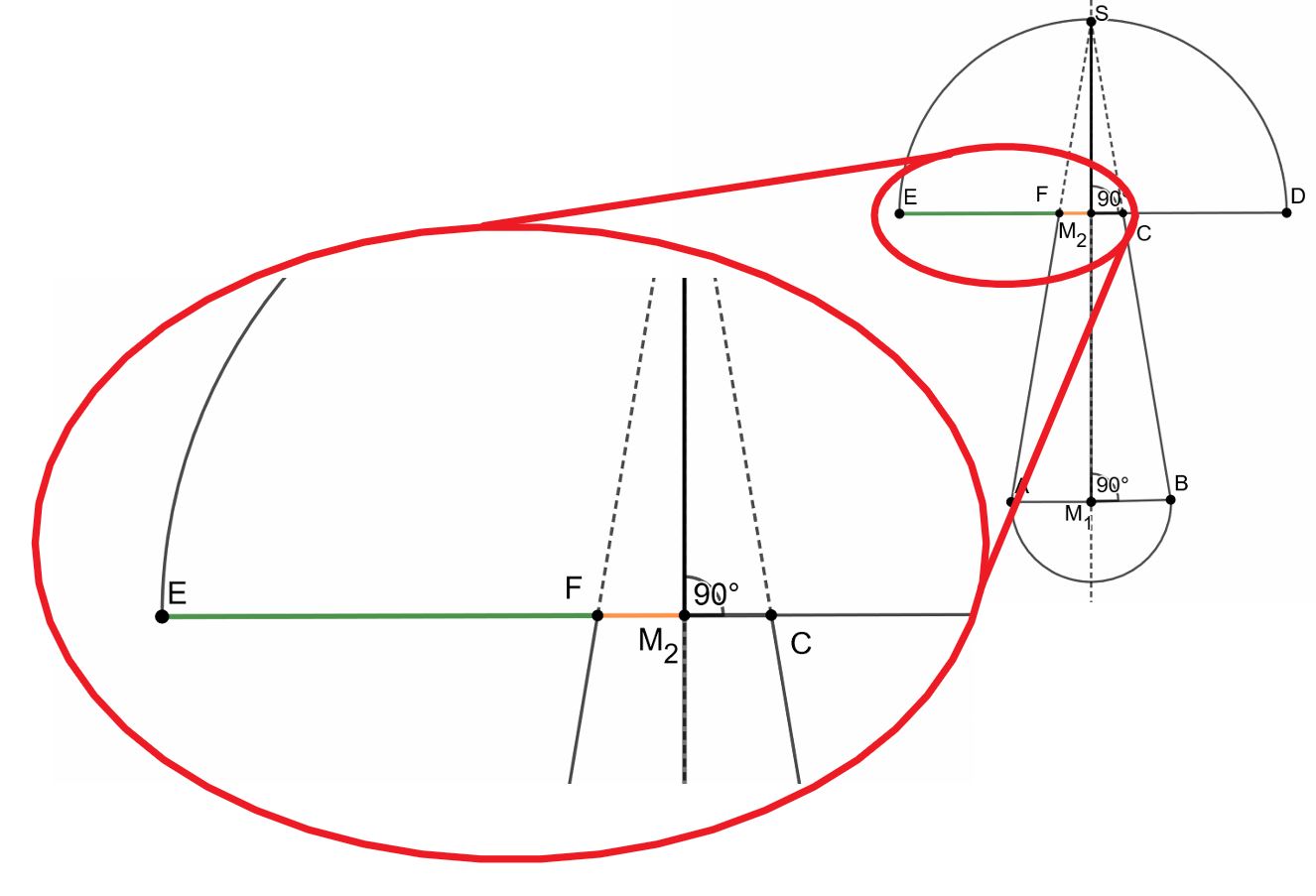
Figur Realschulabschlussprüfung Ausschnitt vergrößert

Gegeben ist die Länge der Strecke $[E M_{2}] = 4 cm$ und die Länge der Strecke $[E F] = 3,2 cm$ .

Anhand der Skizze erkennst du, dass der Punkt $F$ auf der Strecke $[E M_{2}]$ liegt. Deshalb subtrahierst du $E F$ von $E M_{2}$ .

$F M_{2} = E M_{2} - E F = 4 cm - 3,2 cm = 0,8 cm$

Die Strecke $[F M_{2}]$ ist $0,8 cm$ lang.

Länge der Strecke $[S M_{1}]$

Für die Berechnung der Länge der Strecke $[S M_{1}]$ nutzt du den Vierstreckensatz. In deiner Formelsammlung findest du folgende Formel und Abbildung:

$C D : A B = Z C : Z A$

mit $A B | | C D$

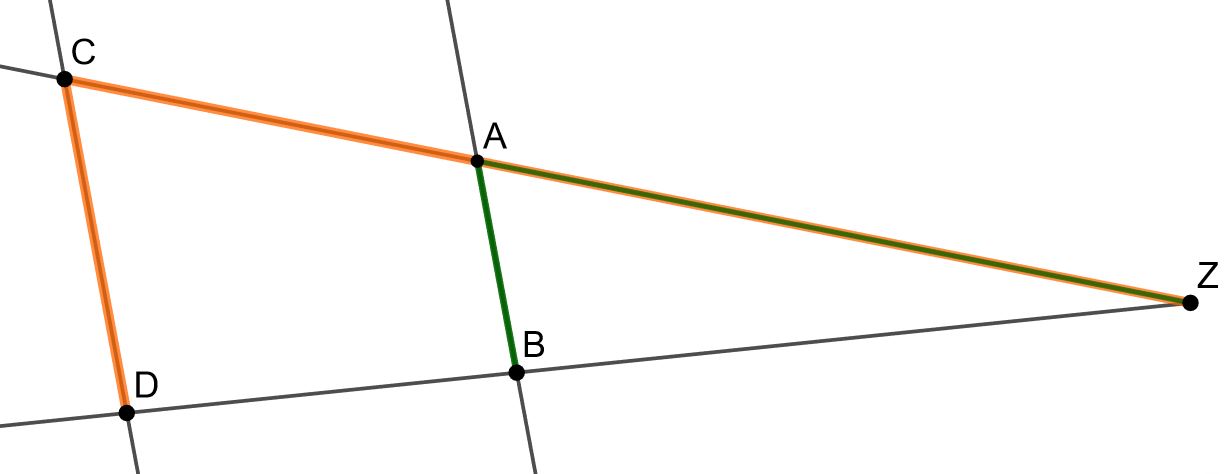
Strahlensatz Vierstreckensatz Grafik aus Formelsammlung

In der gegebenen Figur entspricht die Strecke $C D = M_{1} B$ und $A B = M_{2} C$ . Die Strecke $Z C = M_{1} S$ und $Z A = M_{2} S$ .

Rotationsfigur Realschulabschlussprüfung 2016

Nun setzt du in die Formel ein.

$C D : A B$	$=$	$Z C : Z A$
	↓	Schreibe die Division als Brüche.
$\frac{C D}{A B}$	$=$	$\frac{Z C}{Z A}$
	↓	Setze in die Gleichung ein.
$\frac{4 c m}{0,8 c m}$	$=$	$\frac{S M_{1}}{2 c m}$
	↓	Multipliziere auf beiden Seiten mit $2 cm$ .
$S M_{1}$	$=$	$\frac{4 c m}{0,8 c m} \cdot 2 c m$
	↓	Berechne
$S M_{1}$	$=$	$10 c m$

Die Strecke $[S M_{1}]$ ist $10 cm$ lang.

Lösung zur Teilaufgabe A 3.2

Allgemeines

In der Teilaufgabe A 3.2 betrachtest du den gegebenen Rotationskörper und errechnest dessen Oberflächeninhalt O.

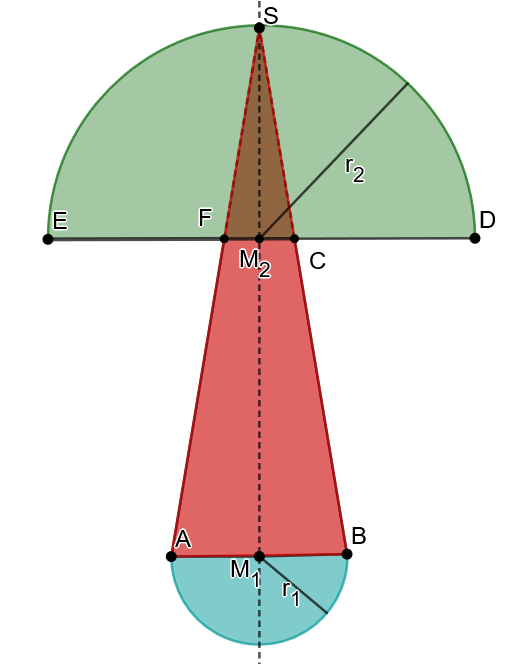
Dieser Rotationskörper entsteht durch Rotation um die Achse $M_{1} S$ .

Im ersten Schritt teilst du den Körper in Teilfiguren auf:

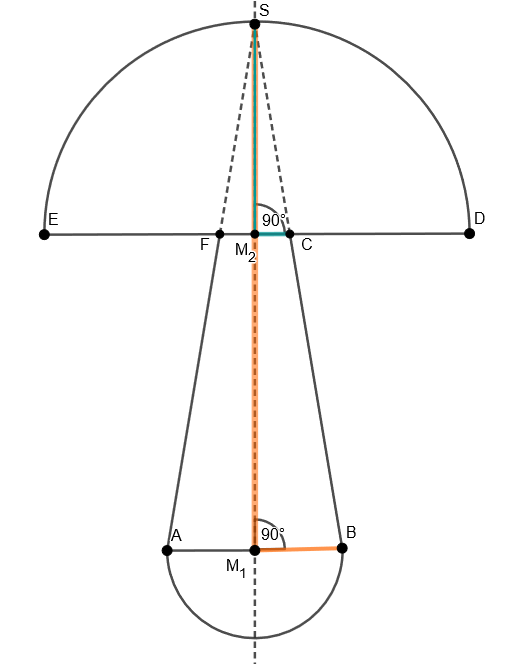
Der Körper besteht aus einer kleinen Halbkugel mit dem Radius $r_{1}$ (im Bild türkis) und einer größeren Halbkugel mit Radius $r_{2}$ (im Bild grün). Außerdem ist ein Kegel mit Radius $r_{1}$ und Höhe $M_{1} S$ (im Bild rot) in der Figur enthalten. Wobei die Spitze des Kegels durch die größere Kugel abgeschnitten wird. Dabei entsteht ein Kegelstumpf.

Für die Berechnung des Oberflächeninhalts ist außerdem noch ein Kreisring von Bedeutung, den man sieht, wenn man von unten auf die größere, grüne Halbkugel schaut.

Teilfiguren Realschulabschlussprüfung 2016

Oberflächeninhalt der kleineren Halbkugel

Im ersten Schritt berechnest du den Oberflächeninhalt der türkisen, kleineren Halbkugel. Den Oberflächeninhalt einer Kugel berechnet man durch folgende Formel.

$O_{Kugel} = 4 \cdot π \cdot r^{2}$

Die Kugel hat den Radius $r_{1} = 2 cm$ . Da du nur eine Halbkugel vorliegen hast, halbierst du den Oberflächeninhalt noch:

$O_{k l . H a l b k u g e l}$	$=$	$\frac{1}{2} \cdot 4 \cdot π \cdot r_{1}^{2}$
	↓	Setze den Radius $r_{1}$ ein.
	$=$	$\frac{1}{2} \cdot 4 \cdot π \cdot {(2 c m)}^{2}$
	↓	Vereinfache soweit wie möglich.
	$=$	$8 \cdot π c m^{2}$
	↓	Berechne und Runde.
	$\approx$	$25,1 c m^{2}$

Der Oberflächeninhalt der kleinen, türkisen Halbkugel beträgt gerundet $25,1 {cm}^{2}$ .

Oberflächeninhalt der größeren Halbkugel

Nun berechnest du den Oberflächeninhalt der größeren, grünen Halbkugel. Für diese Berechnung bestimmst du die Hälfte des Oberflächeninhalts einer ganzen Kugel mit Radius $r_{2} = 4 cm$ .

$O_{g r . H a l b k u g e l}$	$=$	$\frac{1}{2} \cdot O_{g r . K u g e l}$
	↓	Setze die Formel zur Bestimmung des Oberflächeninhaltes der Kugel ein und halbiere ihn.
	$=$	$\frac{1}{2_{}} \cdot 4 \cdot π \cdot r_{2}^{2}$
	↓	Setze den Radius $r_{2}$ ein.
	$=$	$\frac{1}{2} \cdot 4 \cdot π \cdot {(4 c m)}^{2}$
	↓	Vereinfache soweit wie möglich.
	$=$	$32 π c m^{2}$
	↓	Berechne und Runde das Ergebnis
	$\approx$	$100,5 c m^{2}$

Flächeninhalt des Kreisrings

Der Kreisring ist die grüne Fläche, die man sieht, wenn man einen Querschnitt entlang der Strecke $[E D]$ zieht und von unten auf die grüne Halbkugel schaut. Zum einen wird er begrenzt von dem kleinen, roten Kreis mit Radius $F M_{2}$ , zum anderen wird der Kreisring von dem größeren Kreis mit Radius $E M_{2}$ begrenzt. Die rote, kleinere Kreisfläche ist die Schnittfläche mit dem Kegel und darf folglich nicht in den Oberflächeninhalt eingerechnet werden.

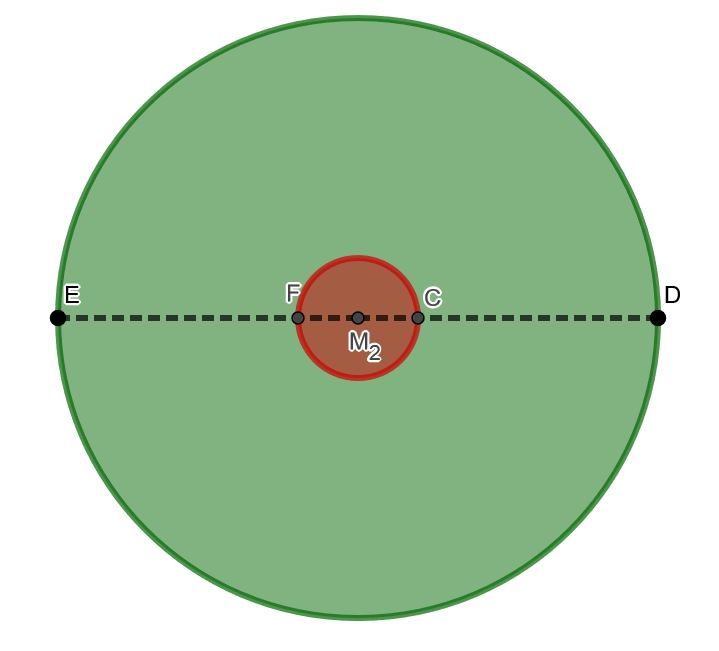
Kreisring Abschlussprüfung Realschule 2016

Um den Flächeninhalt des Kreisring zu bestimmen, subtrahierst du den Flächeninhalt des Kreise mit Radius $E M_{2} = r_{2} = 4 cm$ von dem Flächeninhalt des Kreises mit Radius $F M_{2} = r_{3} = 0,8 cm$ .

$A_{K r e i s r i n g}$	$=$	$π \cdot r_{2}^{2} - π \cdot r_{3}^{2}$
	↓	Setze die beiden Radien ein.
	$=$	$π \cdot {(4 c m)}^{2} - π \cdot {(0,8 c m)}^{2}$
	↓	Vereinfache soweit wie möglich.
	$=$	$16 \cdot π c m^{2} - 0,64 \cdot π c m^{2}$
	↓	Vereinfache weiter.
	$=$	$15,36 \cdot π c m^{2}$
	↓	Berechne und runde auf eine Nachkommastelle.
	$\approx$	$48,2 c m^{2}$

Der Flächeninhalt des Kreisrings beträgt circa $48,2 {cm}^{2}$ .

Oberflächeninhalt des Kegels

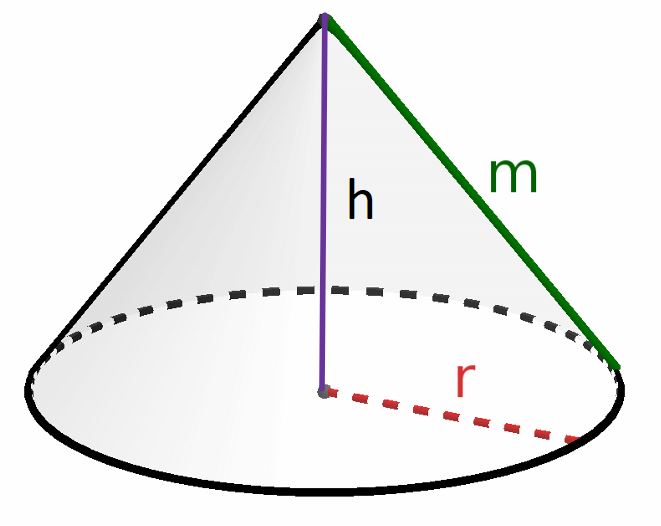
Für den Oberflächeninhalt eines Kegels gilt $O = G + M$

mit Grundfläche $G = r \cdot 2 \cdot π$ und

Mantelfläche $M = r \cdot m \cdot π$ .

Außerdem beschreibt $m$ die Mantellinie und $r$ den Radius.

Für $m$ gilt nach dem Satz des Pythagoras $m = \sqrt{r^{2} + h^{2}}$ .

Mit Hilfe des Radius $r$ und der Höhe $h$ kannst du nun den Oberflächeninhalt allgemein bestimmen.

Für den Oberflächeninhalt des gesamten Rotationskörper sind lediglich die äußeren Oberflächenstücke entscheidend. Infolgedessen fällt die Grundfläche des Kegels für diese Betrachtung weg.

Deshalb erhältst du den Oberflächeninhalt dadurch, dass du die Mantelfläche $M_{Kegel}$ des Kegels errechnest und davon die Mantelfläche der abgegrenzten Kegelspitze $M_{Kegelspitze}$ abziehst.

Es ergibt sich also:

$O_{K e g e l s t u m p f}$	$=$	$M_{K e g e l} - M_{K e g e l s p i t z e}$
	$=$	$r_{K e g e l} \cdot m_{K e g e l} \cdot π - r_{K e g e l s p i t z e} \cdot m_{K e g e l s p i t z e} \cdot π$
	$=$	$r_{K e g e l} \cdot \sqrt{r_{K e g e l}^{2} + h_{K e g e l}^{2}} \cdot π - r_{K e g e l s p i t z e} \cdot \sqrt{r_{K e g e l s p i t z e}^{2} + h_{K e g e l s p i t z e_{}}^{2}} \cdot π$
	$=$	$A M_{1} \cdot \sqrt{{A M_{1}}^{2} + {S M_{1}}^{2}} \cdot π - F M_{2} \cdot \sqrt{{F M_{2}}^{2} + {S M_{2}}^{2}} \cdot π$
	$=$	$2 c m \cdot \sqrt{{(2 c m)}^{2} + {(10 c m)}^{2}} \cdot π - 0,8 c m \cdot \sqrt{{(0,8 c m)}^{2} + {(4 c m)}^{2}} \cdot π$
	$\approx$	$64,1 c m^{2} - 10,3 c m^{2}$
	$=$	$53,8 c m^{2}$

Der Oberflächeninhalt des Kegelstumpfes beträgt gerundet $53, 8 {cm}^{2}$ .

Oberflächeninhalt des gesamten Rotationskörpers

Für den Oberflächeninhalt des gesamten Rotationskörper sind lediglich die äußeren Oberflächenstücke entscheidend.

Deshalb addiert man für die Gesamtoberfläche den Oberflächeninhalt der großen Halbkugel, den Flächeninhalt des Kreisrings, den Oberflächeninhalt des Kegelstumpfs und den Oberflächeninhalt der kleineren Halbkugel.

$O_{Gesamt} = \underset{große Halbkugel}{\underset{⏟}{100,5 {cm}^{2}}} + \underset{Kreisring}{\underset{⏟}{48,3 c m^{2}}} + \underset{Kegelstumpf}{\underset{⏟}{53,8 c m^{2}}} + \underset{kleine Halbkugel}{\underset{⏟}{25,1 c m^{2}}} = 227,7 c m^{2}$

Der Oberflächeninhalt umfasst also $227,7 c m^{2}$ .

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?