Einigen Schülerinnen und Schülern sind hier Fehler unterlaufen. Finde den Fehler!
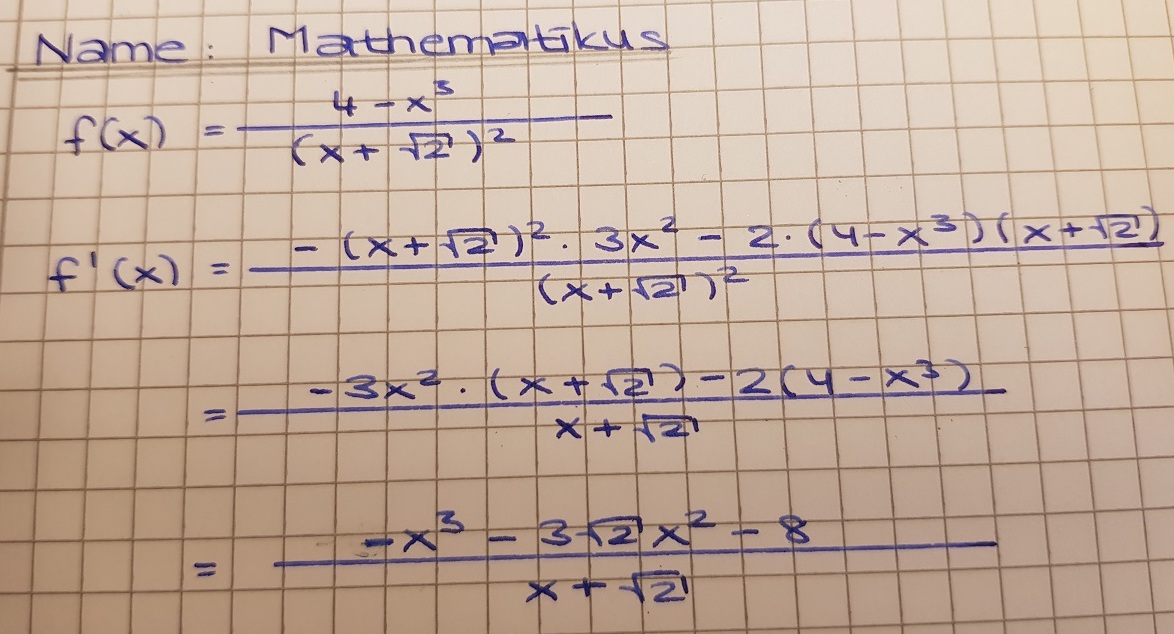
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quotientenregel
Wende die Quotientenregel an, um den Lösungsweg überprüfen zu können.
Vergleichst du die Lösung mit der Aufgabe oben, so siehst du, dass die beiden Ergebnisse nicht übereinstimmen. Bei der Anwendung der Quotientenregel hat Mathematicus das Quadrieren des Nenners vergessen, weshalb seine Lösung fehlerhaft ist.
Hast du eine Frage oder Feedback?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quotientenregel
Tipp: Achte auf die Vorzeichen!
Wende die Quotientenregel an, um den Lösungsweg überprüfen zu können.
Multipliziere den Zähler aus und vereinfache.
Wende den Trigonometrischen Pythagoras an.
Vergleichst du die beiden Lösungswege, so siehst du, dass die beiden Ergebnisse nicht übereinstimmen. Der Fehler hat sich bei Mimi bei der Ableitung des Kosinus eingeschlichen, indem sie das Minus vergessen hat. Im richtigen Lösungsweg siehst du, dass das Minus aus der Anwendung der Quotientenregel und das Minus von der Ableitung des Kosinus zu einem Plus zusammengefasst werden.
Hast du eine Frage oder Feedback?
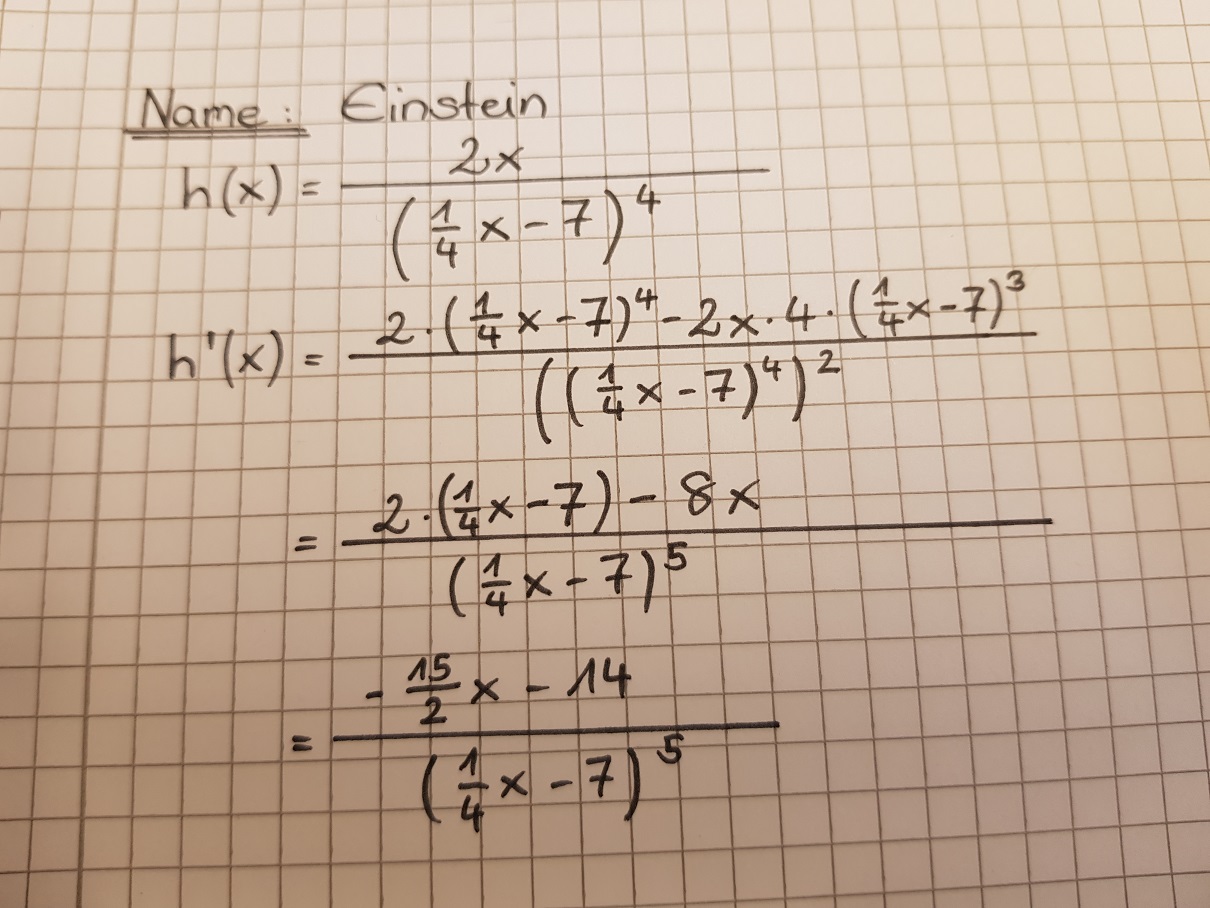
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quotientenregel
Wende die Quotientenregel und die Kettenregel an, um den Lösungsweg überprüfen zu können.
Vergleichst du die beiden Lösungswege, so siehst du, dass die beiden Ergebnisse nicht übereinstimmen. Bei der Anwendung der Kettenregel hat Einstein das Nachdifferenzieren bei der Ableitung des Nenners vergessen. Berücksichtigt man dies, so erhält man durch das Nachdifferenzieren im Zähler den Faktor .
Hast du eine Frage oder Feedback?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quotientenregel
Wende die Quotientenregel an, um den Lösungsweg überprüfen zu können.
Vergleichst du die beiden Lösungswege, so siehst du, dass die beiden Ergebnisse nicht übereinstimmen. Prof. Hut hat bei der Verwendung der Quotientenregel nicht NAZ-ZAN, sondern ZAN-NAZ angewandt.
Zusatz: Betrachtet man die beiden Endresultate, so fällt auf, dass diese sich im Zähler in den Vorzeichen unterscheiden.
Hast du eine Frage oder Feedback?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quetientenregel
Merkregel: In Differenzen und Summen kürzen nur die Dummen.
Wende die Quotientenregel an, um den Lösungsweg überprüfen zu können.
Vergleichst du die beiden Lösungswege, so siehst du, dass die beiden Ergebnisse nicht übereinstimmen. Fiffi hat in ihrer Lösung aus einer Differenz gekürzt und somit die Merkregel nicht beachtet.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
