Aufgaben zur Quotientenregel
Hier kannst du die Anwendung der Quotientenregel üben. In diesen Aufgaben lernst du, wie du den Quotient zweier Funktionen ableiten kannst.
- 1
Bilde von folgenden Funktionen die Ableitung mithilfe der Quotientenregel.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Um diese Aufgabe bearbeiten zu können solltest du Ableitungen und vor allem die Quotientenregel beherrschen.
Wende die Quotientenregel an.
↓ Vereinfachen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Zum Lösen dieser Aufgabe brauchst du Wissen über Ableitungen und die Quotientenregel.
Wende die Quotientenregel an.
↓ Vereinfachen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Um diese Aufgabe lösen zu können solltest du dich mit Ableitungen und der Quotientenregel auskennen.
Wende die Quotientenregel an.
↓ Vereinfachen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Um diese Aufgabe lösen zu können solltest du Ableitungen beherrschen. Vor allem die Quotientenregel und die Kettenregel sind wichtig.
Wende die Quotientenregel an. Wende zudem die Kettenregel auf an.
↓ Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Zum Lösen dieser Aufgabe ist es hilfreich Ableitungen und Quotientenregel zu können.
Wende die Quotientenregel an.
↓ Vereinfachen.
↓ Hast du eine Frage oder Feedback?
- 2
Bilde von folgenden Funktionen die Ableitung mithilfe der Quotientenregel.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quotientenregel
↓ Wende die Quotientenregel an.
↓ Vereinfachen.
↓ Trigonometrischen Phytagoras anwenden.
Hast du eine Frage oder Feedback?
- 3
Leite die folgenden Funktionen auf zwei verschiedene Weisen ab.
Variante 1
Nutze zunächst das Potenzgesetz zur Multiplikation bei gleicher Basis, um den Ausdruck zu vereinfachen.
Jetzt brauchst du die Regel zum Ableiten von Potenzfunktionen. Der Faktor bleibt aufgrund der Faktorregel unverändert.
Zum Schluss musst du die Faktoren vor dem verrechnen.
Variante 2
Eine weitere Möglichkeit, diese Aufgabe zu lösen, ist das Anwenden der Produktregel.
Fasse den Term weiter zusammen.
Man erkennt, dass das Ergbnis in beiden Fällen ist.
Hast du eine Frage oder Feedback?
Tipp: Neben der Produktregel kannst du auch die Potenzgesetze anwenden, um dir das Ableiten zu vereinfachen.
Variante 1
Leite die Funktion mit Hilfe der Regel zum Ableiten von Potenzfunktionen ab.
Variante 2
Mit Hilfe des Potenzgesetzes zu negativen Exponenten kannst du den Term auch als Bruch schreiben.
Jetzt kannst du die Quotientenregel anwenden.
Vereinfache nun den Zähler noch weiter.
Kürze den Zähler und Nenner mit .
Man erkennt, dass das Ergbnis in beiden Fällen ist.
Hast du eine Frage oder Feedback?
Tipp: Die erste Möglichkeit ist, die Regel zum Ableiten von Potenzfunktionen zu verwenden. Andererseits kannst du aber auch die Potenzgesetze anwenden und anschließend mit der Quotientenregel ableiten.
Vereinfache den Term noch weiter.
Jetzt brauchst du die Regel zum Ableiten von Potenzfunktionen.
Variante 2
Eine weiter Möglichkeit ist, jeden Summanden für sich abzuleiten. Nutze bei dem ersten und letzten Summanden die Quotientenregel.
Fasse die Zähler noch weiter zusammen.
Kürze den ersten Bruch mit .
Die Ableitung ist bei beiden Varianten an allen Stellen gleich (Nullfunktion).
Du hast eine weitere Variante gefunden diese Aufgabe zu lösen? Dann schreib uns gerne in die Kommentare oder füge deine Variante der Lösung hinzu.
Hast du eine Frage oder Feedback?
Tipp: Du kannst den Bruchterm erst kürzen und zusammenfassen und dann Ableiten, oder die Quotientenregel anwenden.
Variante 1
Im Zähler der Funktion findest du die dritte binomische Formel.
Stelle den Term im Zähler zunächst in Klammerschreibweise dar.
Hier kannst du im Zähler und Nenner den Term kürzen.
Jetzt brauchst du die Regel zum Ableiten von Potenzfunktionen.
Variante 2
Du kannst die Funktion auch mit Hilfe der Quotientenregel ableiten und fasse den Zähler noch weiter zusammen:
Multipliziere die mit der .
Multipliziere die und jeweils in die Klammern.
Löse die Klammer auf.
Fasse und weiter zusammen.
Klammere im Zähler eine aus.
Im Zähler der Funktion findest du die zweite binomische Formel.
Wenn du den Term im Zähler in Klammerschreibweise darstellst, kannst du Nenner und Zähler bis auf die vollständig kürzen.
Man erkennt, dass das Ergbnis in beiden Fällen ist.
Du hast eine weitere Variante gefunden diese Aufgabe zu lösen? Dann schreib uns gerne in die Kommentare oder füge deine Variante der Lösung hinzu.
Hast du eine Frage oder Feedback?
Tipp: Du kannst die Aufgabe auf zwei Wegen lösen, entweder mit einer binomischen Formel oder der Quotientenregel.
Variante 1
Löse die Aufgabe mit Hilfe der Produktregel und Summenregel.
Multipliziere in den Zähler des Bruchs und forme um.
Kürze und schreibe als .
Verrechne beide .
Variante 2
Überlege dir, welche Beziehungen du zwischen dem Tangens und dem Sinus bzw. dem Kosinus kennst und vereinfache die Funktion zunächst.
Schreibe als .
Multipliziere in den Zähler des Bruchs.
Bringe auf den selben Nenner.
Wende den Trigonometrischen Pythagoras an.
Jetzt kannst du die Funktion mit Hilfe der Quotientenregel ableiten.
Fasse den Zähler noch weiter zusammen.
Schreibe als .
Man erkennt, dass das Ergbnis in beiden Fällen ist.
Du hast eine weitere Variante gefunden diese Aufgabe zu lösen? Dann schreib uns gerne in die Kommentare oder füge deine Variante der Lösung hinzu.
Hast du eine Frage oder Feedback?
Tipp: Du kannst diese Funktion entweder mithilfe der Produktregel und Summenregel ableiten, oder sie zuerst mithilfe der Beziehungen zwischen Tangens, Sinus und Kosinus.
- 4
Gegeben sind die Funktionen und .
Leite auf zwei verschiedene Arten ab.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quotientenregel
Quotientenregel und Potenzgesetze
Es gibt zwei verschiedene Wege, die Ableitung von zu bestimmen.
Variante 1
Bei der ersten Möglichkeit nutzt du die Quotientenregel.
Vereinfache nun den Zähler.
Variante 2
Bei der zweiten Möglichkeit nutzt du zunächst das Potenzgesetz zu negativen Exponenten, um den Funktionsterm umzuformen.
Jetzt brauchst du die Regel zum Ableiten von Potenzfunktionen.
Zuletzt kannst du den Term wieder als Quotienten schreiben.
Beide Varianten liefern das Endergebnis bzw. .
Hast du eine Frage oder Feedback?
Bestimme die Ableitung der Funktion .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kettenregel
Tipp: Löse die Aufgabe mit Hilfe der Kettenregel.
Ableiten einer Wurzelfunktion
Die Ableitung von bestimmst du mithilfe der Regel zum Ableiten von Potenzfunktionen und der Kettenregel.
Verwende das Potenzgesetz zu Einheitsbrüchen im Exponenten.
Leite mit der Regel zum Ableiten von Potenzfunktionen und der Kettenregel ab.
Kürze mit 2.
Verwende das Potenzgesetz zu negativen Exponenten.
Verwende das Potenzgesetz zu Einheitsbrüchen im Exponenten.
Die gesuchte Funktion ist also .
Hast du eine Frage oder Feedback?
Bilde die Verkettungen und .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kompositionen
Tipp: Bilde die Kompositionen bzw. Verkettungen der Funktionen und .
Wenn du nicht genau weißt, was eine Komposition (oder Verkettung) von Funktionen ist, dann schau doch hier nach.
Kompositionen von Funktionen
Um die erste der beiden Kompositionen der Funktionen und zu erhalten, musst du in einsetzen.
Die andere Komposition der Funktionen und erhältst du, wenn du in einsetzt.
Ergänzung
Man sieht, dass sich die Ergebnisse unterscheiden: .
Es kommt also bei der Verkettung von Funktionen auf die Reihenfolge an!
Hast du eine Frage oder Feedback?
Leite die Kompositionen aus Teilaufgabe c) ab.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quotientenregel
Tipp: Nutze für zuerst die Quotientenregel und dann die Kettenregel und für erst die Kettenregel und dann die Quotientenregel.
Teil 1
Wende die Quotientenregel auf und dabei die Kettenregel auf an, um die Ableitung zu bestimmen.
Vereinfache nun den Zähler.
Verwende das Potenzgesetz zu negativen Exponenten, um in den Nenner zu schreiben.
Verwende das Potenzgesetz zur Multiplikation bei gleicher Basis.
Addiere und im Exponenten.
Teil 2
Wende hier die Kettenregel auf und dabei die Quotientenregel auf an, um die Ableitung zu bestimmen.
Kürze die .
Verwende das Potenzgesetz zu negativen Exponenten, um in den Nenner zu schreiben.
Verwende das Potenzgesetz zu Einheitsbrüchen im Exponenten.
Fasse beide Faktoren zu einem Bruch zusammen.
Die gesuchten Funktionen sind und
Du hast eine weitere Variante gefunden diese Aufgabe zu lösen? Dann schreib uns gerne in die Kommentare oder füge deine Variante der Lösung hinzu.
Hast du eine Frage oder Feedback?
Leite die Kompositionen aus Teilaufgabe c) ohne Anwendung der Quotientenregel ab.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kettenregel
Tipp: Deine Ergebnisse aus Teilaufgabe a) und b) können dir hier helfen.
Setze und ein.
Setze ein.
Fasse beide Faktoren zu einem Bruch zusammen und vereinfache.
Verwende die Potenzgesetze.
Teil 2
Um die Ableitung von zu bestimmen, wendest du ebenfalls die Kettenregel an.
Setze und ein.
Setze ein.
Fasse beide Faktoren zu einem Bruch zusammen.
Die gesuchten Funktionen sind also und
Hast du eine Frage oder Feedback?
- 5
Einigen Schülerinnen und Schülern sind hier Fehler unterlaufen. Finde den Fehler!
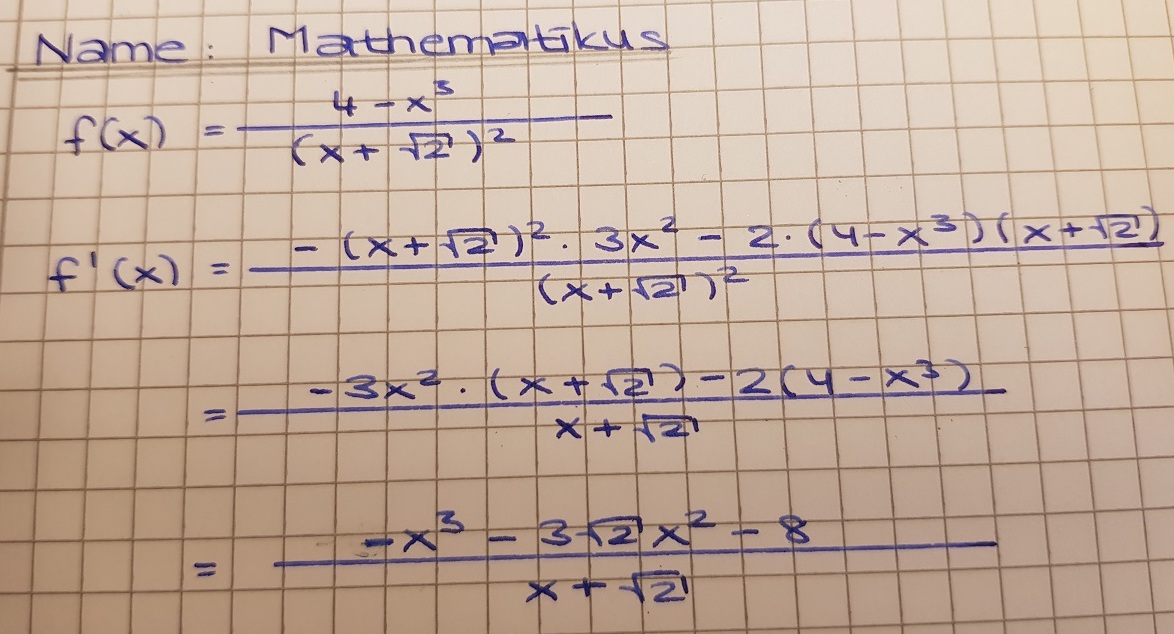
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quotientenregel
Wende die Quotientenregel an, um den Lösungsweg überprüfen zu können.
Vergleichst du die Lösung mit der Aufgabe oben, so siehst du, dass die beiden Ergebnisse nicht übereinstimmen. Bei der Anwendung der Quotientenregel hat Mathematicus das Quadrieren des Nenners vergessen, weshalb seine Lösung fehlerhaft ist.
Hast du eine Frage oder Feedback?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quotientenregel
Tipp: Achte auf die Vorzeichen!
Wende die Quotientenregel an, um den Lösungsweg überprüfen zu können.
Multipliziere den Zähler aus und vereinfache.
Wende den Trigonometrischen Pythagoras an.
Vergleichst du die beiden Lösungswege, so siehst du, dass die beiden Ergebnisse nicht übereinstimmen. Der Fehler hat sich bei Mimi bei der Ableitung des Kosinus eingeschlichen, indem sie das Minus vergessen hat. Im richtigen Lösungsweg siehst du, dass das Minus aus der Anwendung der Quotientenregel und das Minus von der Ableitung des Kosinus zu einem Plus zusammengefasst werden.
Hast du eine Frage oder Feedback?
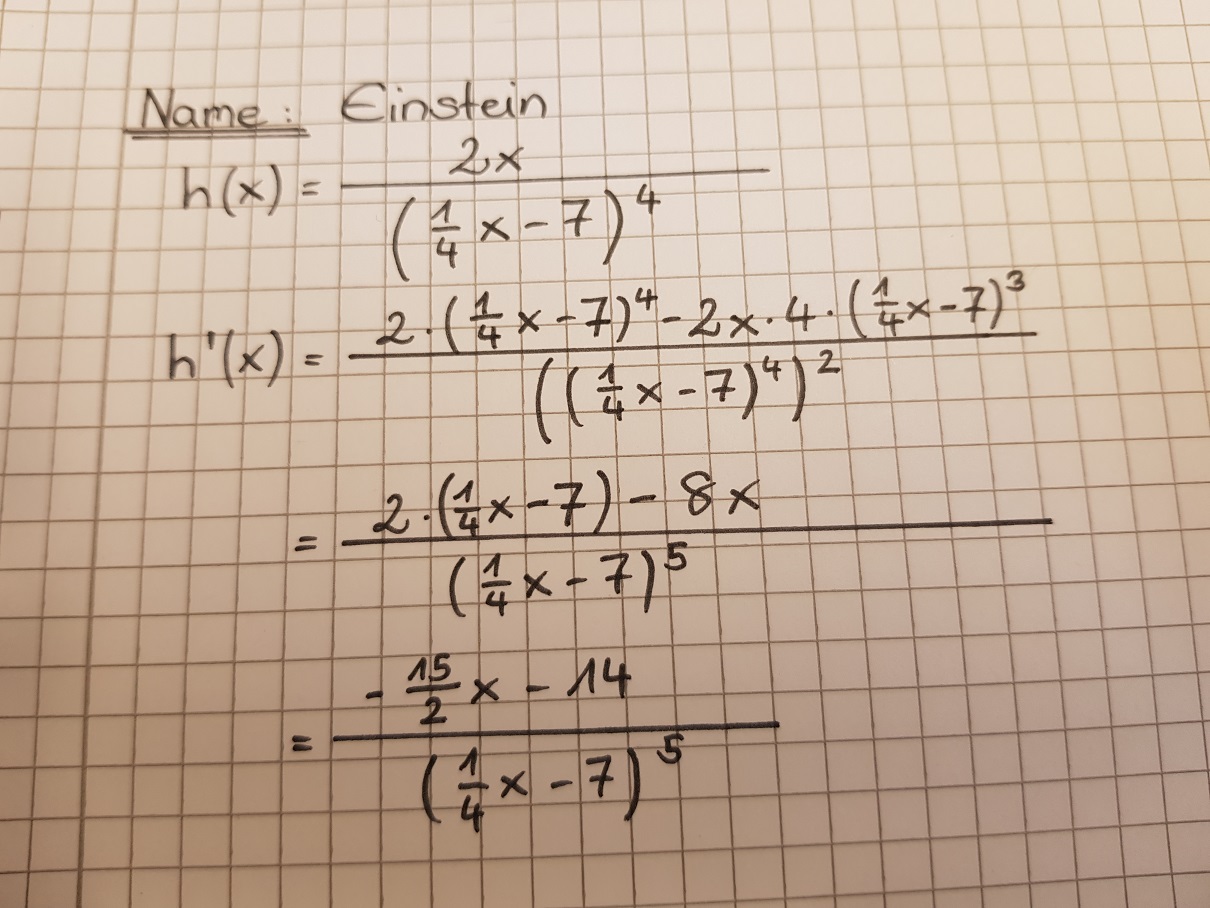
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quotientenregel
Wende die Quotientenregel und die Kettenregel an, um den Lösungsweg überprüfen zu können.
Vergleichst du die beiden Lösungswege, so siehst du, dass die beiden Ergebnisse nicht übereinstimmen. Bei der Anwendung der Kettenregel hat Einstein das Nachdifferenzieren bei der Ableitung des Nenners vergessen. Berücksichtigt man dies, so erhält man durch das Nachdifferenzieren im Zähler den Faktor .
Hast du eine Frage oder Feedback?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quotientenregel
Wende die Quotientenregel an, um den Lösungsweg überprüfen zu können.
Vergleichst du die beiden Lösungswege, so siehst du, dass die beiden Ergebnisse nicht übereinstimmen. Prof. Hut hat bei der Verwendung der Quotientenregel nicht NAZ-ZAN, sondern ZAN-NAZ angewandt.
Zusatz: Betrachtet man die beiden Endresultate, so fällt auf, dass diese sich im Zähler in den Vorzeichen unterscheiden.
Hast du eine Frage oder Feedback?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quetientenregel
Merkregel: In Differenzen und Summen kürzen nur die Dummen.
Wende die Quotientenregel an, um den Lösungsweg überprüfen zu können.
Vergleichst du die beiden Lösungswege, so siehst du, dass die beiden Ergebnisse nicht übereinstimmen. Fiffi hat in ihrer Lösung aus einer Differenz gekürzt und somit die Merkregel nicht beachtet.
Hast du eine Frage oder Feedback?
- 6
Welche der angegebenen Ableitungen gehören zu der jeweiligen Funktion?
Denke an die Quotientenregel und versuche mit ihrer Hilfe auf die richtige Lösung zu kommen. Der Nenner von wird hier mit und der Zähler mit bezeichnet.
Hier:
Ursprungsfunktion:
Nenner der Ursprungfunktion:
Zähler der Ursprungsfunktion:
Ableitung des Nenners:
Ableitung des Zählers:
Setze nun die einzelnen Funktionen in die Quotientenregel ein:
Vergleichst du die Lösung mit den Antwortmöglichkeiten, so siehst du, dass nicht stimmen kann, da im Zähler steht anstatt im Nenner.
Du siehst auch, dass die Ableitungsfunktion die falsche Lösung ist. Das Minus, das du durch die Anwendung der Quotientenregel erhältst, fehlt hier.
Betrachtest du die Potenzgesetze mit negativen Exponenten näher, so fällt dir auf, dass du das der Lösung in den Zähler ziehen kannst. Dazu kannst du das auch als schreiben. Also ist ebenso eine Lösung.
Die richtigen Antworten sind:
Die falschen Antworten sind:
Hast du eine Frage oder Feedback?
Tipp: Beachte neben der Quotientenregel auch das Potenzgesetz zu negativen Exponenten.
Berechnung mit der Quotientenregel
Wende die Quotientenregel und passende Umformungen an, um auf die richtigen Lösungen zu kommen. Der Nenner von wird mit und der Zähler mit bezeichnet.
Hier:
Ursprungsfunktion:
Zähler der Ursprungsfunktion:
Nenner der Ursprungsfunktion:
Ableitung des Zählers:
Ableitung des Nenners:
Setze nun die einzelnen Funktionen in die Quotientenregel ein:
Vereinfache den Zähler.
Vereinfache den Zähler weiter.
Die Lösung erhältst du also direkt mit der Quotientenregel.
Überprüfung der übrigen Antwortmöglichkeiten
Um zu überprüfen, ob auch noch andere Antwortmöglichkeiten richtig sind, musst du nun versuchen, dein Ergebnis so umzuformen, dass es mit den anderen Antwortmöglichkeiten übereinstimmt.
Im Nenner steht die erste binomische Formel:
Somit erhältst du nun auch die Lösung .
Wende nun auf dein Ergebnis der Quotientenregel das Potenzgesetz zu negativen Exponenten an:
Du erhältst also eine dritte richtige Lösung: .
Überprüfe nun, ob auch die letzte Antwortmöglichkeit richtig ist.
Im Nenner wurde wieder die erste binomische Formel angewandt. Nun musst du noch die Zähler vergleichen.
Die Zähler unterscheiden sich und auch durch Umformen kommst du nicht von auf . Somit ist die Antwortmöglichkeit falsch. (Falls du auf diese Lösung kommst, solltest du dir die Quotientenregel nochmal genau anschauen, denn dann hast du wahrscheinlich fälschlicherweise im Zähler addiert statt subtrahiert.)
Zusammenfassung
Die richtigen Lösungen sind:
Die falsche Antwort ist:
Hast du eine Frage oder Feedback?
Tipp: Achte auch auf binomische Formeln und das Potenzgesetz zu negativen Exponenten.
Denke an die Quotientenregel und versuche mit dem Ausschlussprinzip auf die richtige Lösung zu kommen. Der Zähler von wird mit und den Nenner von wird mit bezeichnet.
Betrachte den Nenner in der Quotientenregel:
Hier:
Ursprungsfunktion:
Nenner der Ursprungsfunktion:
Nenner der Ableitung:
Vergleiche die Nenner aus den Antwortmöglichkeiten mit dem von dir gefundenen Nenner der Ableitung. Du stellst fest, dass die Antwortmöglichkeiten und im Nenner jeweils stehen haben.
Da nicht gleich ist und da du auch durch Kürzen nicht von auf kommst, sind diese beiden Antworten also falsch.
Dir bleiben nun noch die Antwortmöglichkeiten und . Wende jetzt das Potenzgesetz zu negativen Exponenten an.
Die beiden Antwortmöglichkeiten sind gleich. Prüfe nun, ob es die richtigen Lösungen sind.
Nutze hierfür die Quotientenregel:
Berechne und ziehe das Minus vor den Bruch.
Das Ergebnis der Ableitung mit der Quotientenregel zeigt also, dass es die richtigen Lösungen sind.
Die richtigen Antworten sind:
Die falschen Antworten sind:
Hast du eine Frage oder Feedback?
Tipp: Betrachte den Nenner der Lösungen. Denke auch an das Potenzgesetz zu negativen Exponenten.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
