Wichtige Eigenschaften des Nenners
Der Nenner eines Bruches darf nicht den Wert 0 haben.
Wenn man den Nenner eines Bruches größer macht (und den Zähler dabei nicht ändert), wird der Wert des Bruchs kleiner.
Was bedeutet der Nenner?
Wenn man einen Bruch als Geteilt-Aufgabe oder Division betrachtet, ist der Nenner der Divisor.
Beispiel: ist dasselbe wie .
Denn statt des Bruchstrichs kann man immer auch das Geteilt-durch-Zeichen ":" schreiben.
Im Kreisdiagramm
Wenn man sich einen Bruch im Kreisdiagramm (oder einer anderen graphischen Darstellung) anschaulich vorstellt, dann sagt der Nenner des Bruches, in wie viele Teile man sich bei diesem Bruch ein Ganzes aufgeteilt denken muss.
Beispiel Nenner 3
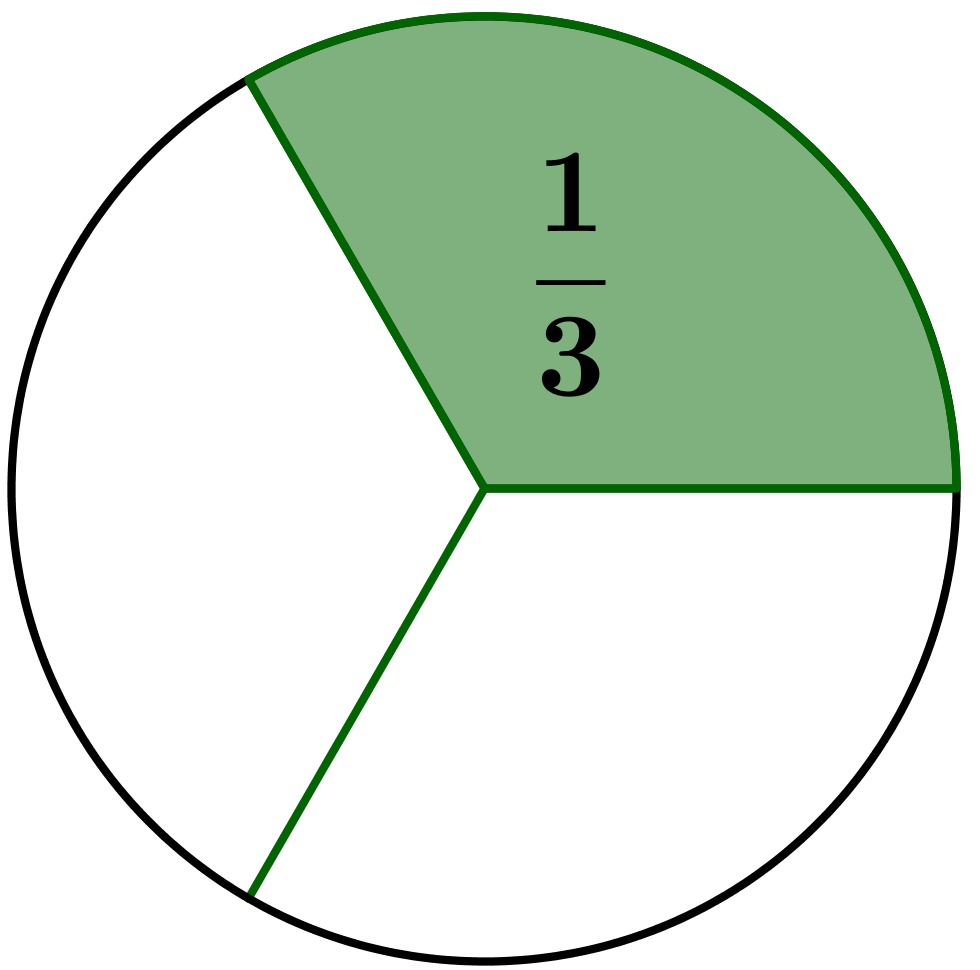
Das Ganze ist in 3 Teile aufgeteilt.
Jedes der Teile ist des Ganzen.
Beispiel Nenner 10
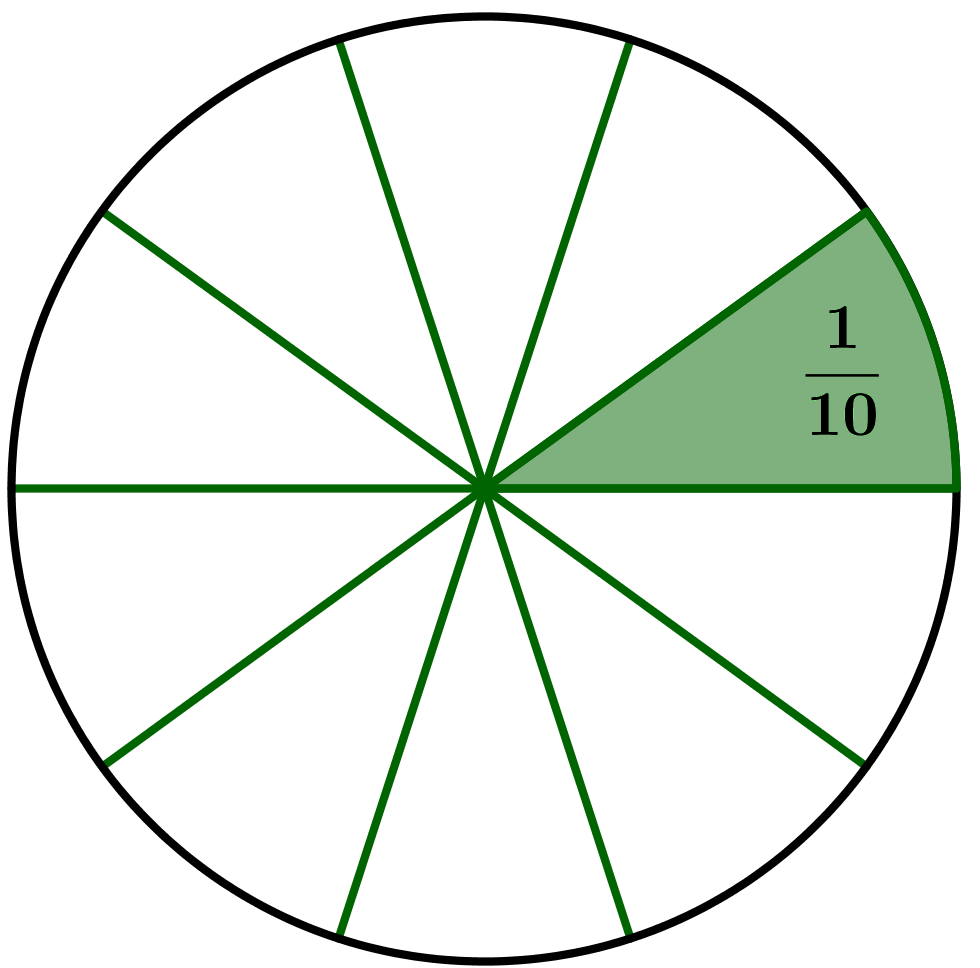
Das Ganze ist in 10 Teile aufgeteilt.
Jedes der Teile ist des Ganzen.
Der Nenner gibt die Art der Anteile an, und der Zähler sagt, wie viele es sind; daher kann man sagen:
Der Nenner benennt die Art der Anteile, der Zähler zählt sie.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:

