Die Winkelfunktionen Sinus, Kosinus und Tangens sind die wichtigsten trigonometrischen Funktionen.
Sinus, Kosinus und Tangens beschreiben das Verhältnis von Seitenlängen in einem rechtwinkligen Dreieck in Abhängigkeit von einem der spitzen Winkel. Sie sind folgendermaßen definiert.
Dabei bezeichnet man als "Ankathete" die Kathete, die zusammen mit der Hypotenuse den Winkel einschließt. Die "Gegenkathete" ist die Kathete, die dem Winkel gegenüberliegt (siehe Bild).
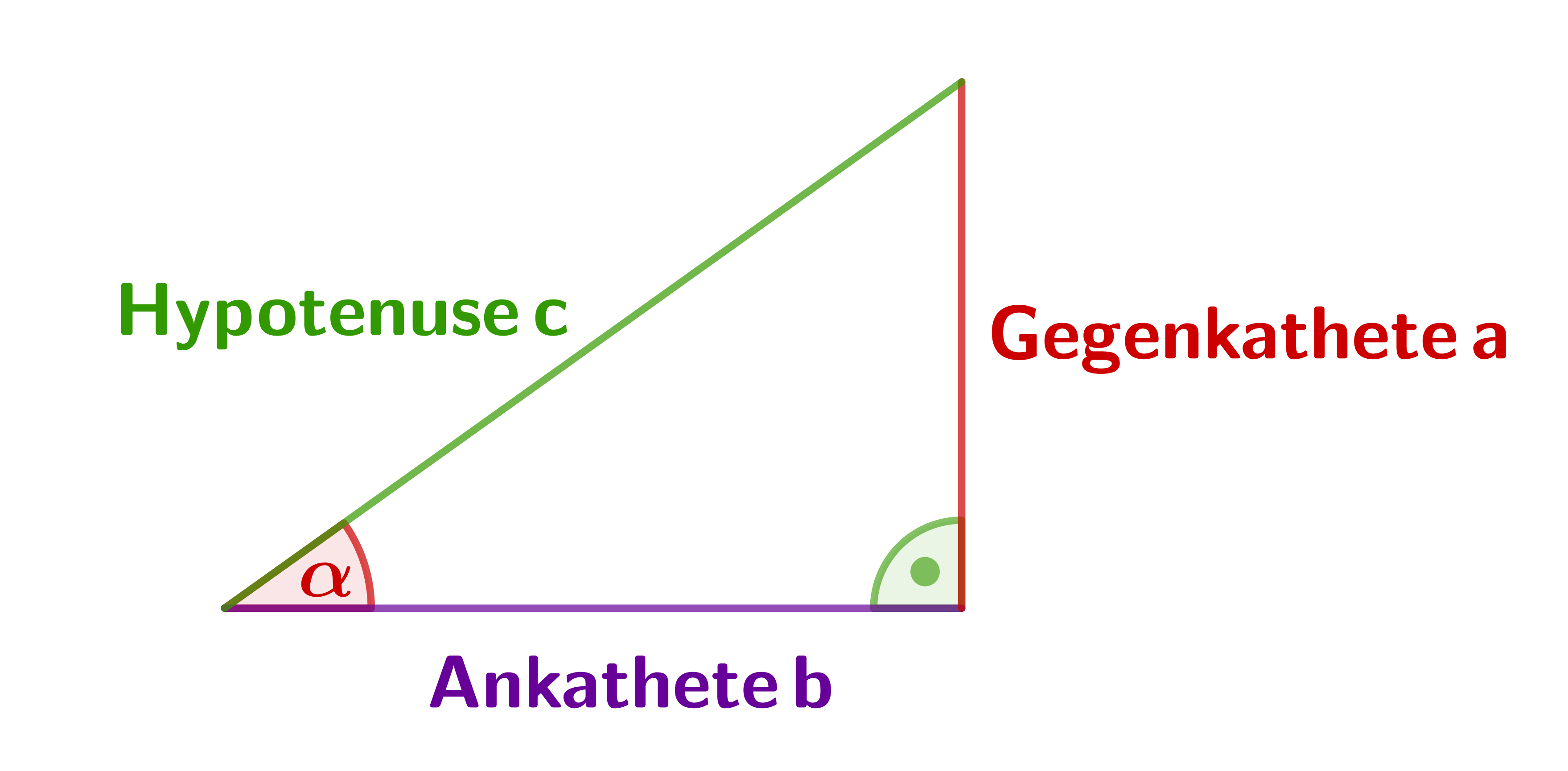
Die "Ankathete" wird hier im Bild mit einem , die "Gegenkathete" mit einem und die Hypotenuse mit einem bezeichnet.
Beachte: Die Seite liegt gegenüber dem Winkel , gegenüber und gegenüber . Wobei in diesem Beispiel der rechte Winkel ist.

Folgende Winkelbeziehungen ergeben sich daraus:
Wichtige Funktionswerte
Die folgende Wertetabelle zeigt die Funktionswerte des Kosinus, Sinus und Tangens:
Achtung: Im Fall entsteht kein Dreieck, da der nicht definiert ist. Siehe dazu Trigonometrie am Einheitskreis.
Abhängigkeiten
Wenn du von einem rechtwinkligen Dreieck eine Seite und einen Winkel gegeben hast, kannst du mithilfe der trigonometrischen Funktionen die restlichen Seiten berechnen.
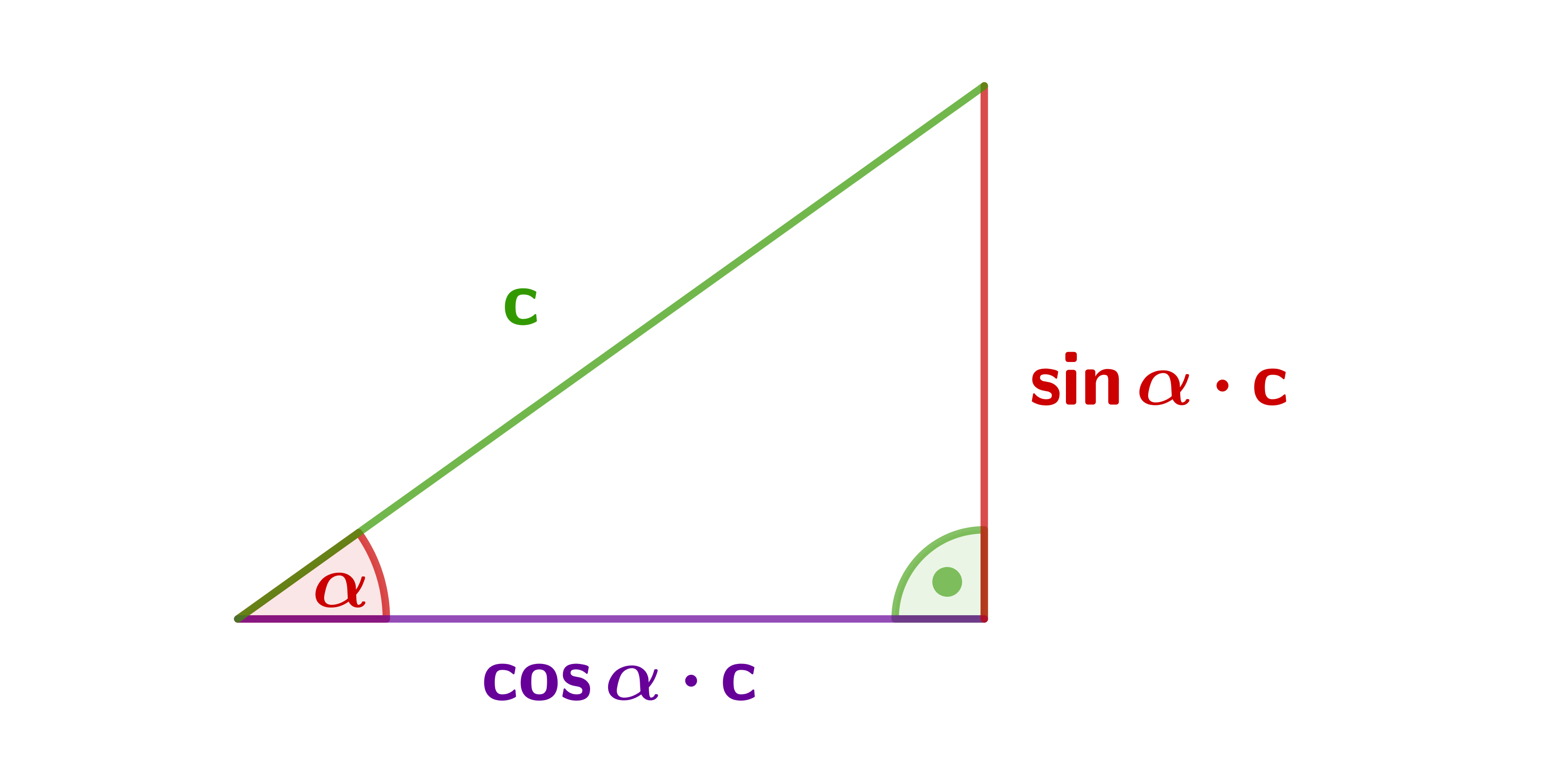
Hypotenuse ist gegeben.
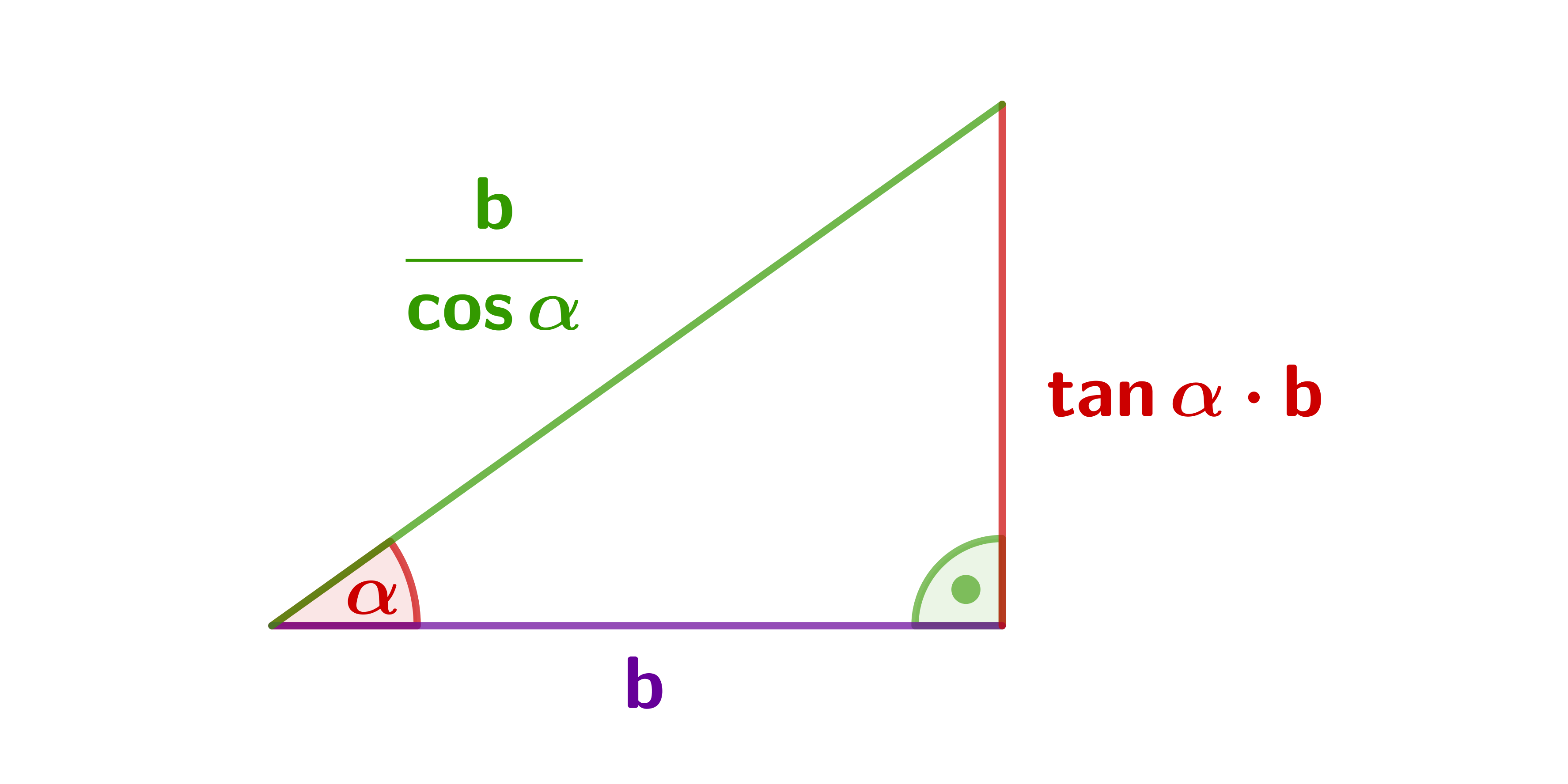
Ankathete ist gegeben.
Gegenkathete ist gegeben.
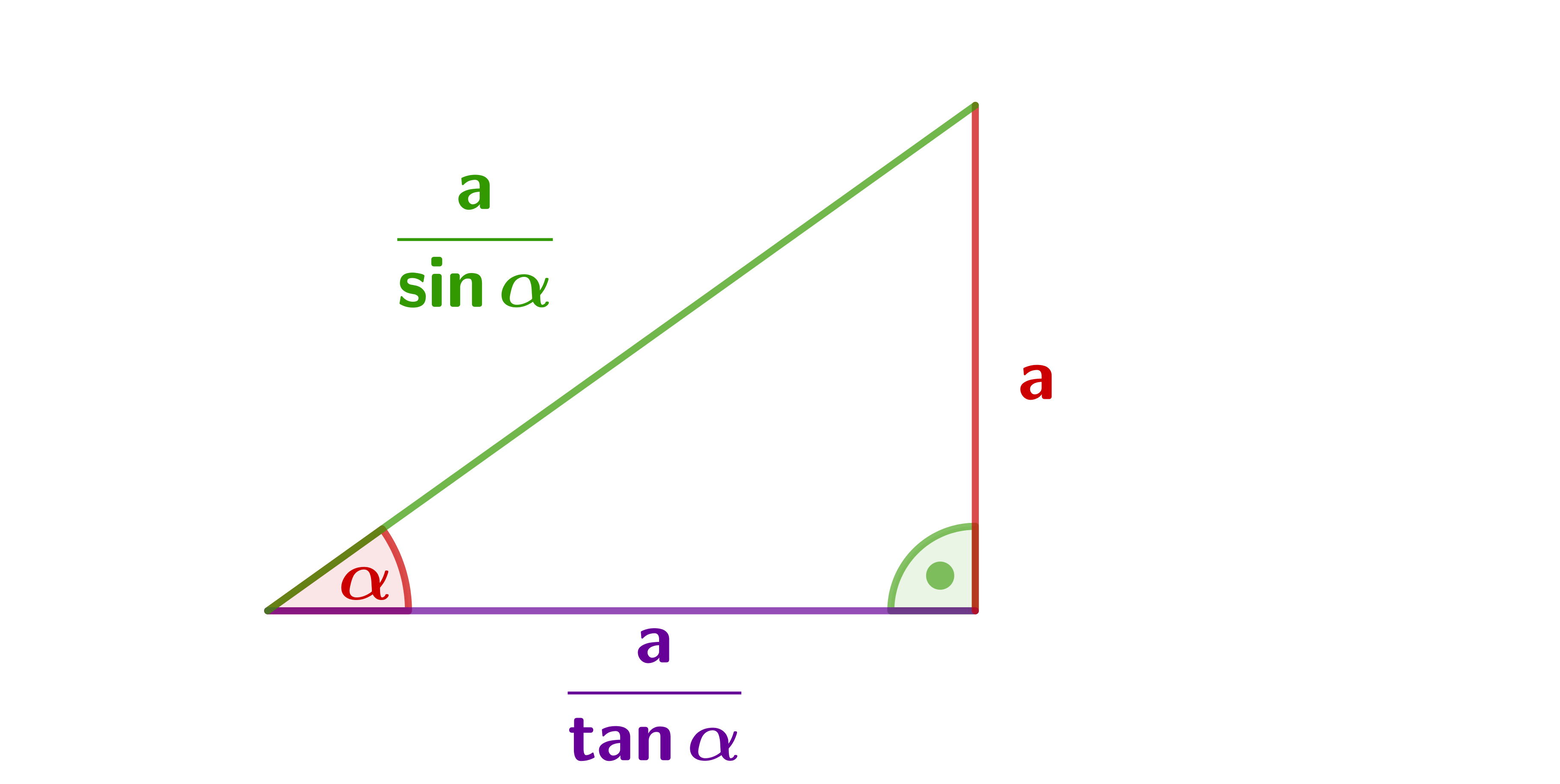
Diese Formeln erhält man, indem man die Definitionen von Sinus, Kosinus und Tangens je nach , und auflöst.
Im ersten Fall, wenn die Hypotenuse gegeben ist, geht das wie folgt.
Die weiteren Fälle ergeben sich ebenso.
Beispiel
Von einem bei rechtwinkligen Dreieck ist die Länge der Hypotenuse und der Winkel bekannt (erstes Schaubild).
Dann lassen sich die Längen der Ankathete und der Gegenkathete mithilfe des Sinus und des Kosinus berechnen:
Rechenregeln
Es gibt einige Rechenregeln zu Sinus, Kosinus und Tangens. Hier werden besprochen:
Tangens als Quotient von Sinus und Kosinus,
der trigonometrische Pythagoras,
die Additionstheoreme.
Tangens als Quotient von Sinus und Kosinus
Direkt über die Definition von oben erhält man für den Tangens folgende alternative Darstellung:
Die Korrektheit dieser Gleichung kannst du auch einfach nachrechnen:
Trigonometrischer Pythagoras
Aus der Definition am Einheitskreis folgt aus dem Satz des Pythagoras direkt:
Eine ausführliche Erklärung findest du im Video weiter unten.
Additionstheoreme
Die Additionstheoreme ermöglichen es, den Sinus und den Kosinus einer Summe zu berechnen:
Weitere Beziehungen zwischen Sinus, Kosinus und Tangens
Im Artikel Beziehungen trigonometrischer Funktionen findest du weitere Beziehungen der Funktionen.
Trigonometrie am Einheitskreis
Die im Artikel dargestellten Winkelbeziehungen kannst du dir auch am Einheitskreis verdeutlichen. Mehr zu diesem Thema kannst du hier lesen: Trigonometrie am Einheitskreis.
Sinus-, Kosinus- und Tangensfunktion
Sinus, Kosinus und Tangens kannst du auch als Funktionen darstellen. Mehr dazu findest du im Artikel Sinusfunktion und Kosinusfunktion oder Tangensfunktion.
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Sinus, Kosinus und Tangens im rechtwinkligen Dreieck
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
