Die Asymptote ist eine Kurve (häufig sogar eine Gerade), an die sich der Graph einer Funktion immer mehr annähert.
"Annähern" bedeutet dabei, dass der Abstand zwischen der Asymptote und dem Funktionsgraphen beliebig klein wird, wenn man
weit weg genug vom Ursprung entlang der x-Achse, oder
entlang der y-Achse
geht.
Achtung! Es kann auch passieren, dass dieser Abstand irgendwann gleich null wird (also, dass die Funktion gleich ihrer Asymptote ist).
Häufig spricht man vom Verhalten im Unendlichen der Funktion, wenn man sie immer weiter weg vom Ursprung entlang der x-Achse betrachtet.
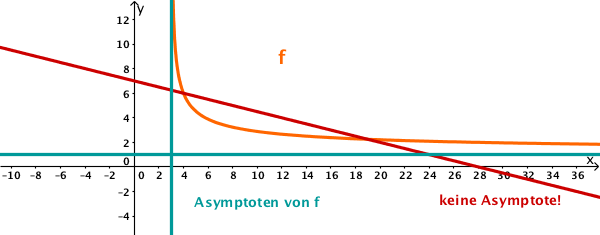
Sind Funktionsgraph und Asymptote immer nah aneinander?
Es kann passieren, dass der Funktionsgraph und die Asymptote in einem Abschnitt auseinandergehen. Genau so können sie sich manchmal berühren oder sogar schneiden.
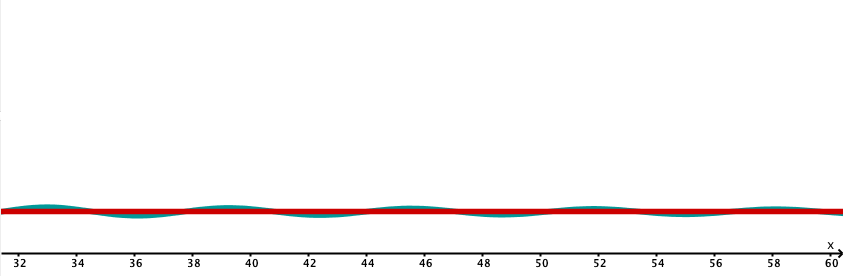
Das folgende Beispiel veranschaulicht eine Funktion, die ihre Asymptote unendlich oft schneidet!
Hier sieht man nur, dass die Funktion um die Gerade bei schwingt.
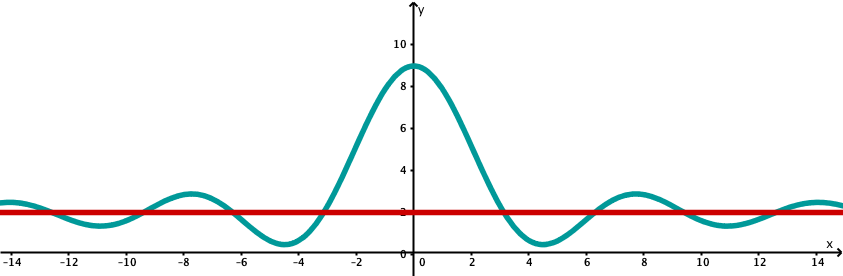
Wenn man in positive Richtung entlang der x-Achse geht wird deutlich, dass die Asymptote der Funktion ist.
Unterscheidung von Asymptoten
Man unterscheidet zwischen vier Arten von Asymptoten:
Waagrechte Asymptote
Diese sind Geraden, die parallel zur x-Achse verlaufen. Diese sind genau die konstanten Funktionen.
Eine Funktion kann höchstens zwei waagrechte Asymptoten haben, nämlich wenn
ganz groß wird (also wenn gegen geht) oder,
wenn ganz klein wird (also gegen geht)
Waagerechte Asymptote bei :
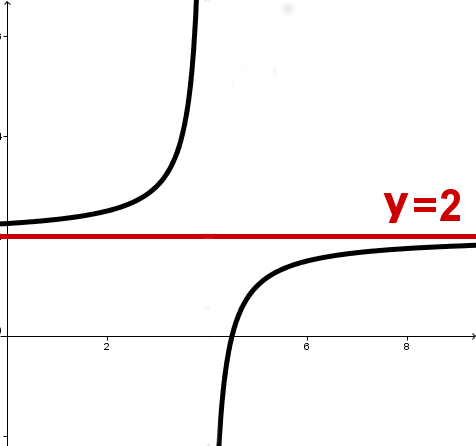
Senkrechte Asymptote (Unendlichkeitsstelle):
Diese sind Geraden, die parallel zur y-Achse verlaufen und werden auch als Polstellen bezeichnet.
Die Funktion aus dem obigen Beispiel hat auch eine senkrechte Asymptote.
Senkrechte Asymptote bei .

Schiefe Asymptote
Bei einer schiefen Asymptote sind weder - noch -Wert konstant.
Die Asymptote wird durch eine allgemeinere Geradengleichung angegeben.
Schiefe Asymptote mit Geradengleichung .
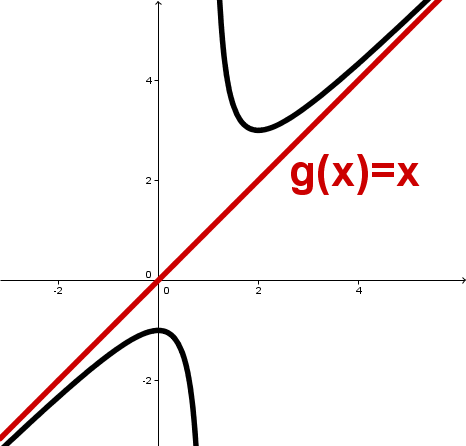
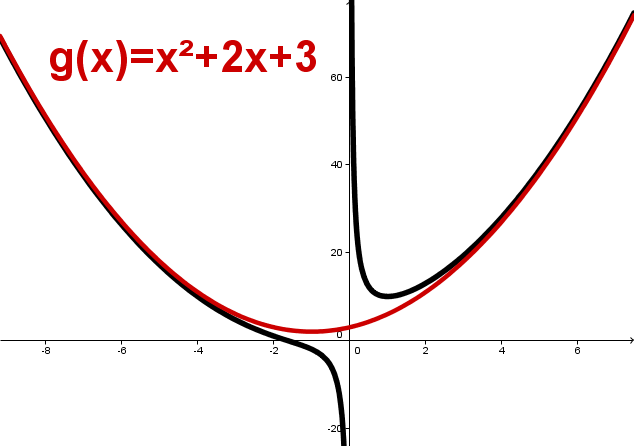
Kurvenförmige Asymptote
Der Graph einer Funktion kann sich einem anderen Funktionsgraphen als einer Geraden annähern.
Bei gebrochenrationalen Funktionen lässt sich ihre Asymptote gut berechnen.
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Berechnen von Asymptoten
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
