Die Nullstellenform ist eine von vier verschiedenen Möglichkeiten zur Darstellung einer quadratischen Funktion. Diese Möglichkeiten sind:
Die allgemeine Form:
Die Normalform
Die Scheitelpunktsform:
Die Nullstellenform:
Der Öffnungsfaktor ist dabei bei jeder der Darstellungsmöglichkeiten einer Funktion gleich.
Aufbau der Nullstellenform
Wie der Name Nullstellenform schon sagt, sind die Nullstellen dafür sehr wichtig.
Oben kannst du bereits erkennen, dass auch der Öffnungsfaktor der quadratischen Funktion für die Nullstellenform eine wichtige Rolle spielt.
Ausgehend von diesen Werten kannst du drei Fälle unterscheiden:
1. Fall: Zwei verschiedene Nullstellen
Die Nullstellenform lautet:
Zum Funktionsgraph im Beispiel:
In der Graphik siehst du, dass Nullstellen bei und hat.
Wie du den Öffnungsfaktor bestimmst, erfährst du weiter unten im Artikel. Hier ist der Öffnungsfaktor .
Deswegen ist der Funktionsterm von in Nullstellenform:
.
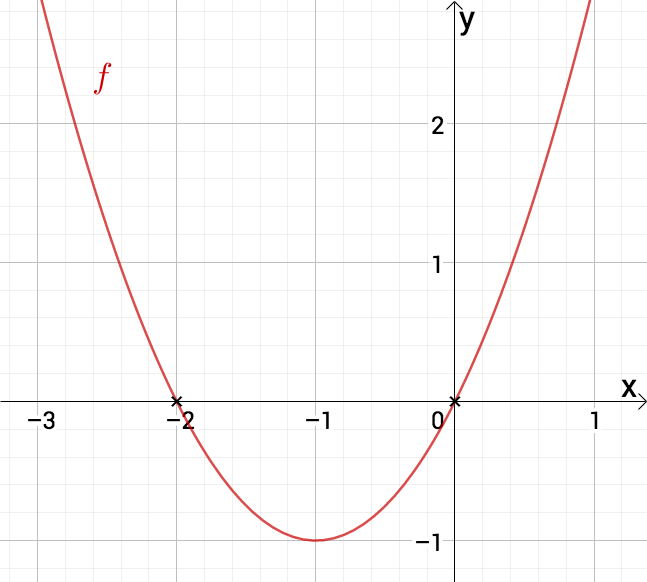
Die Funktion hat zwei verschiedene Nullstellen und .
2. Fall: Eine Nullstelle mit zweifacher Vielfachheit
ist eine doppelte Nullstelle, und deshalb ist . Du kannst also für einsetzen und :
Zum Funktionsgraph im Beispiel:
In der Graphik siehst du, dass eine doppelte Nullstelle bei hat.
Wie du den Öffnungsfaktor bestimmst, erfährst du weiter unten im Artikel. Hier ist der Öffnungsfaktor .
Deswegen ist der Funktionsterm von in Nullstellenform:
.
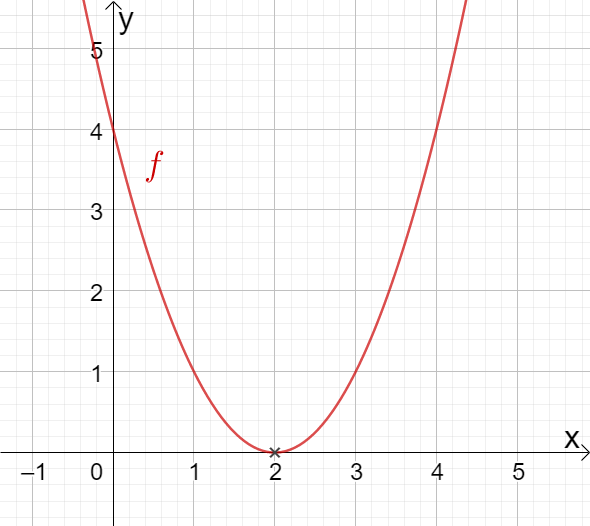
Die Funktion hat eine Nullstelle mit Vielfachheit .
3. Fall: Keine Nullstelle
Es gibt keine Nullstellenform.
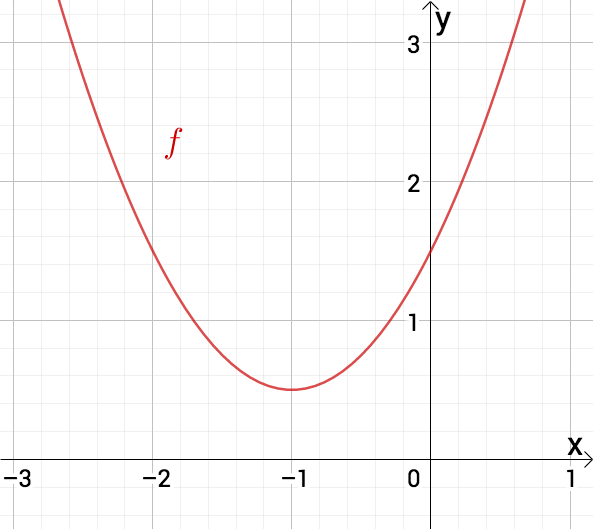
Die Funktion hat keine Nullstelle.
Video zu den Nullstellen quadratischer Funktionen
Laden
Veranschaulichung
Die folgende Grafik stellt dar, wie sich die Nullstellenform einer Funktion in Abhängigkeit vom Funktionsgraphen und ihrer Scheitelpunktsform verändert.
Scheitelpunktsform
Zur Erinnerung: Die allgemeine Form der Scheitelpunktsform ist
Die Scheitelpunktsform der Funktion ist abhängig von den Parametern , und . Du siehst die Scheitelpunktsform in der linken oberen Ecke der Grafik.
Graph
Der abgebildete Graph der Funktion verändert sich in Abhängigkeit von den einzelnen Parametern der Scheitelpunktsform.
Nullstellenform
Die Nullstellenform ist abgebildet in der linken unteren Ecke der Grafik. Du siehst, wie sich die Nullstellenform ändert, wenn sich die einzelnen Parameter verändern.
Bestimmung der Nullstellenform
Zu einer gegebenen Funktionsgleichung in einer anderen Darstellungsform oder einem Graphen soll die Nullstellenform bestimmt werden.
Das schematische Vorgehen ist folgendermaßen:
Bestimme die Nullstellen und und deren Vielfachheit
Bestimme den Öffnungsfaktor
Setze in den passenden der oben genannten drei Fälle ein
Das erste Beispiel behandelt, wie du eine Funktionsgleichung von Scheitelpunktsform in Nullstellenform umrechnest. Das zweite Beispiel zeigt, wie du aus einem gegebenen Funktionsgraphen die zugehörige Nullstellenform bestimmst.
Beispiel 1: Bestimmung aus Scheitelpunktsform
Beispiel 2: Bestimmung aus Funktionsgraph
Weitere Beispiele
Informationen aus der Nullstellenform
Aus einer gegebenen Nullstellenform kannst du auch Informationen herauslesen. Diese sind die Nullstellen , und der Öffnungsfaktor .
Das nächste Beispiel zeigt, wie du diese Informationen gewinnen kannst.
Vertiefung: Linearfaktordarstellung
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Nullstellenform
