Das Volumen geometrischer Objekte wird mit Methoden der analytischen Geometrie ausgerechnet.
Volumen eines Parallelotops (Spat, Parallelflach)
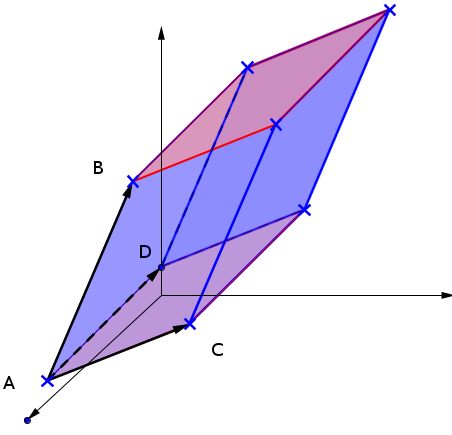
Das Volumen eines Parallelotops, das mit Punkten aufgespannt wird, berechnet sich nach folgender Formel aus der Determinante (oder des Spatprodukts) der drei aufspannenden Vektoren.
Das Volumen eines Parallelotops wird berechnet, indem man einen beliebigen Eckpunkt wählt und alle 3 von dort ausgehenden Richtungsvektoren
berechnet.
Der Betrag der Determinante aus den 3 Richtungsvektoren ist das Volumen.
Die Reihenfolge der Vektoren spielt keine Rolle wenn man das Ganze in den Betrag schreibt. Hier kannst du alle Rechenregeln für Determinanten finden.
Beispiele
Berechne das Volumen des Parallelotops, welches
Laden
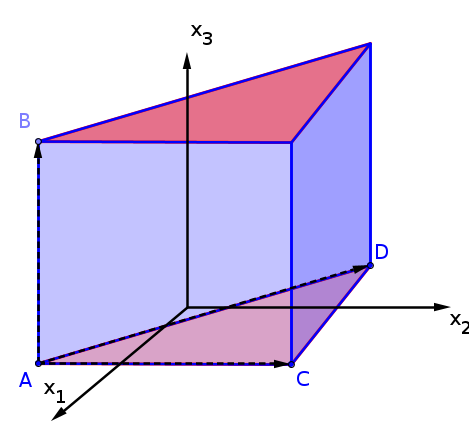
Volumen eines Prismas (mit einem Dreieck als Grundfläche)
Das Volumen eines Prismas mit einem Dreieck als Grundfläche ist das halbe Volumen eines Parallelotops.
Also ist das Volumen
Bei allgemeinen Prismen kann man die Grundfläche immer in Dreiecke zerlegen und man kann das Volumen der einzelnen Prismen mit Dreiecken als Grundseite berechnen.
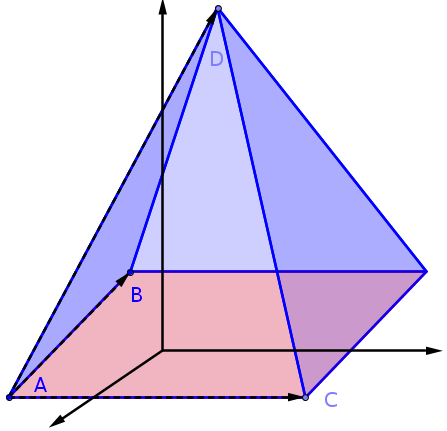
Volumen einer Pyramide (Parallelogramm als Grundfläche)
Das Volumen einer Pyramide lässt sich berechnen als
Beispiele
Berechne das Volumen der Pyramide, welche
Laden
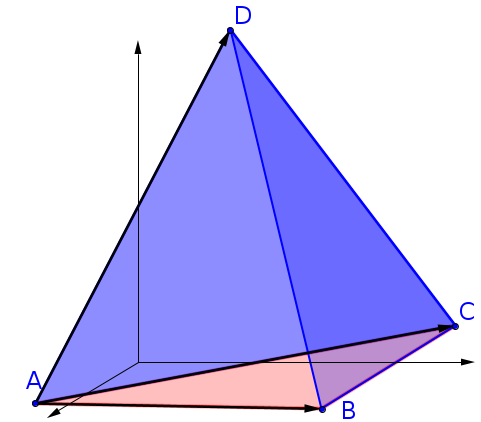
Volumen eines Tetraeders
Ein Tetraeder ist eine Pyramide , die als Grundseite ein Dreieck hat. Ein Tetraeder wird durch vier Punkte eindeutig bestimmt.
Seien diese Punkte, dann ist das Volumen :
Die Formel für das Volumen eines Tetraeders sieht der Volumenformel einer Pyramide sehr ähnlich.
Der Skalierungsfaktor (statt wie bei der Pyramide) kommt daher, dass die Grundfläche hier ein Dreieck und kein Parallelogramm ist.
Das Volumen des Tetraeders ist also mal so groß, wie das der Pyramide.
Beispiele
Berechne das Volumen des Tetraeders, welches
Laden
