Um den Verbindungsvektor zwischen zwei Punkten A und B zu berechnen, muss man den Ortsvektor zu Punkt A vom Ortsvektor zu Punkt B subtrahieren.
"Spitze minus Fuß"
Im Zweidimensionalen:
Im Dreidimensionalen:
Der Vektor hat also beim Minuend seine Spitze und beim Subtrahend seinen Fuß.
Formel
wobei den Ursprung bezeichnet und somit den Vektor vom Ursprung zu dem Punkt darstellt.
Berechne den Vektor, der seine Spitze in und seinen Fuß in hat.
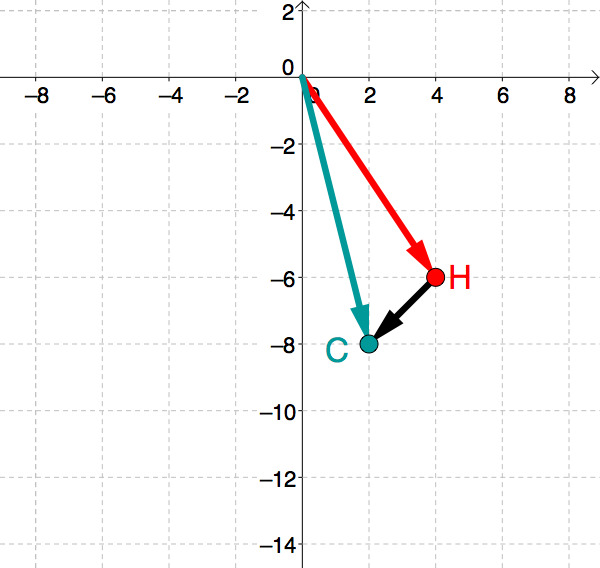
Spitze (hier: ) minus Fußpunkt (hier: ) | |||
| ↓ | |||
Berechne den Vektor, der seinen Fuß in und seine Spitze in hat.
Spitze (hier: ) minus Fußpunkt (hier: ) | |||
| ↓ | |||
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Berechnung eines Vektors zwischen zwei Punkten
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
