Aufgaben zur Berechnung eines Vektors zwischen zwei Punkten
Hier findest du Aufgaben zur Berechnung eines Vektors zwischen zwei Punkten. Übe dabei sowohl im zwei- als auch im dreidimensionalen Koordinatensystem.
- 1
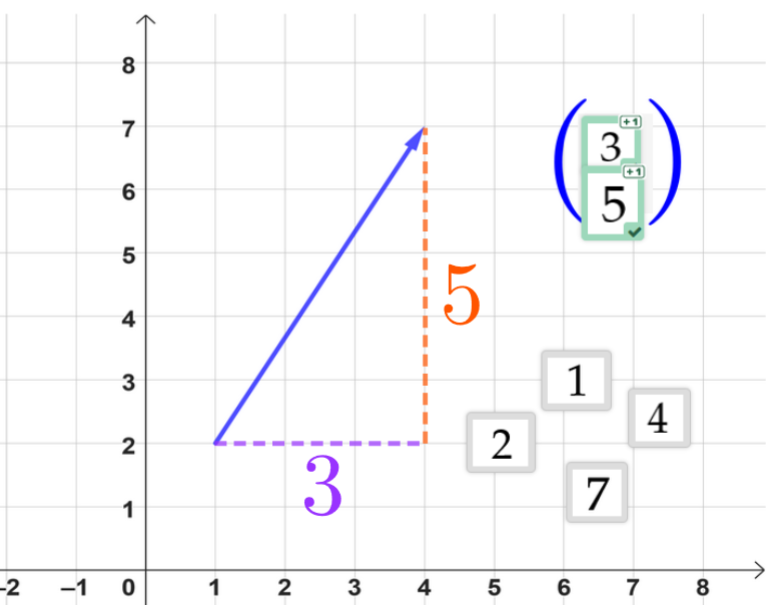
Vektor gesucht
Bestimme den Vektor, indem du die richtigen Koordinaten zuordnest.
- 2
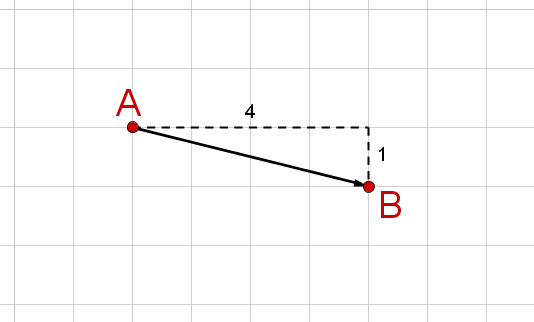
Berechne den Verbindungsvektor vom jeweils ersten Punkt zum zweiten Punkt.
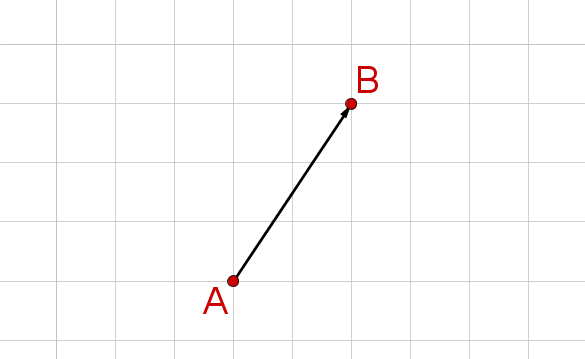
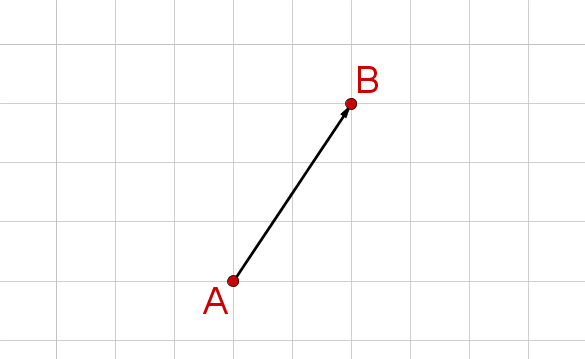
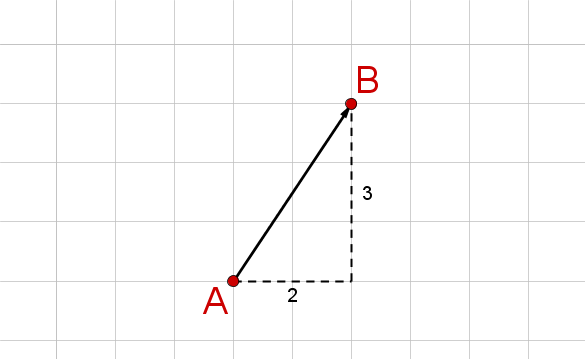
- 3
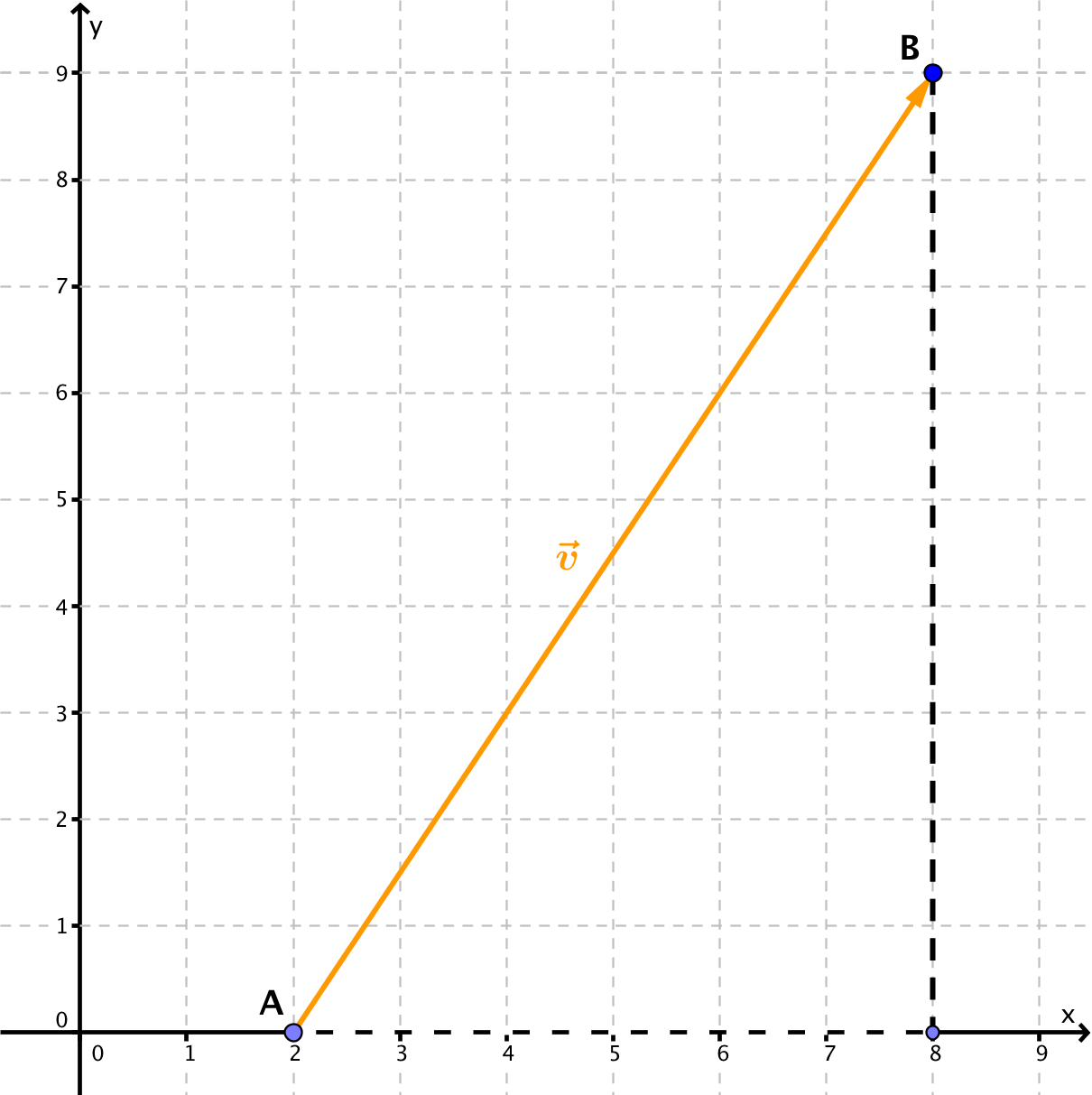
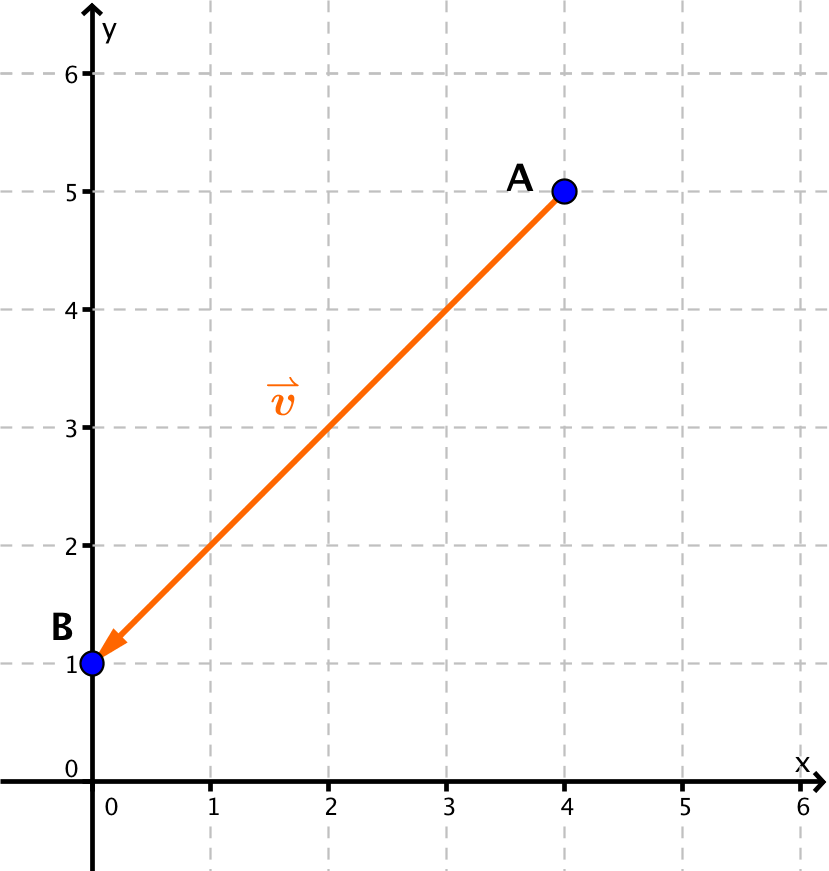
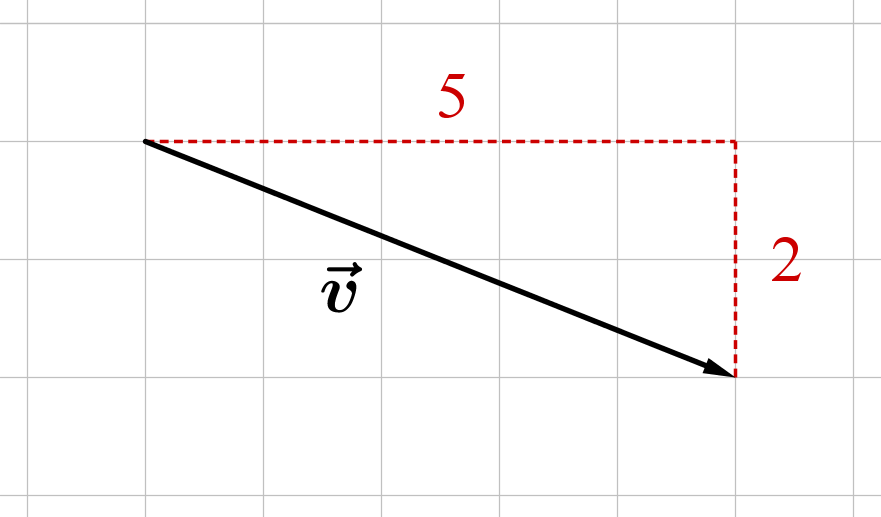
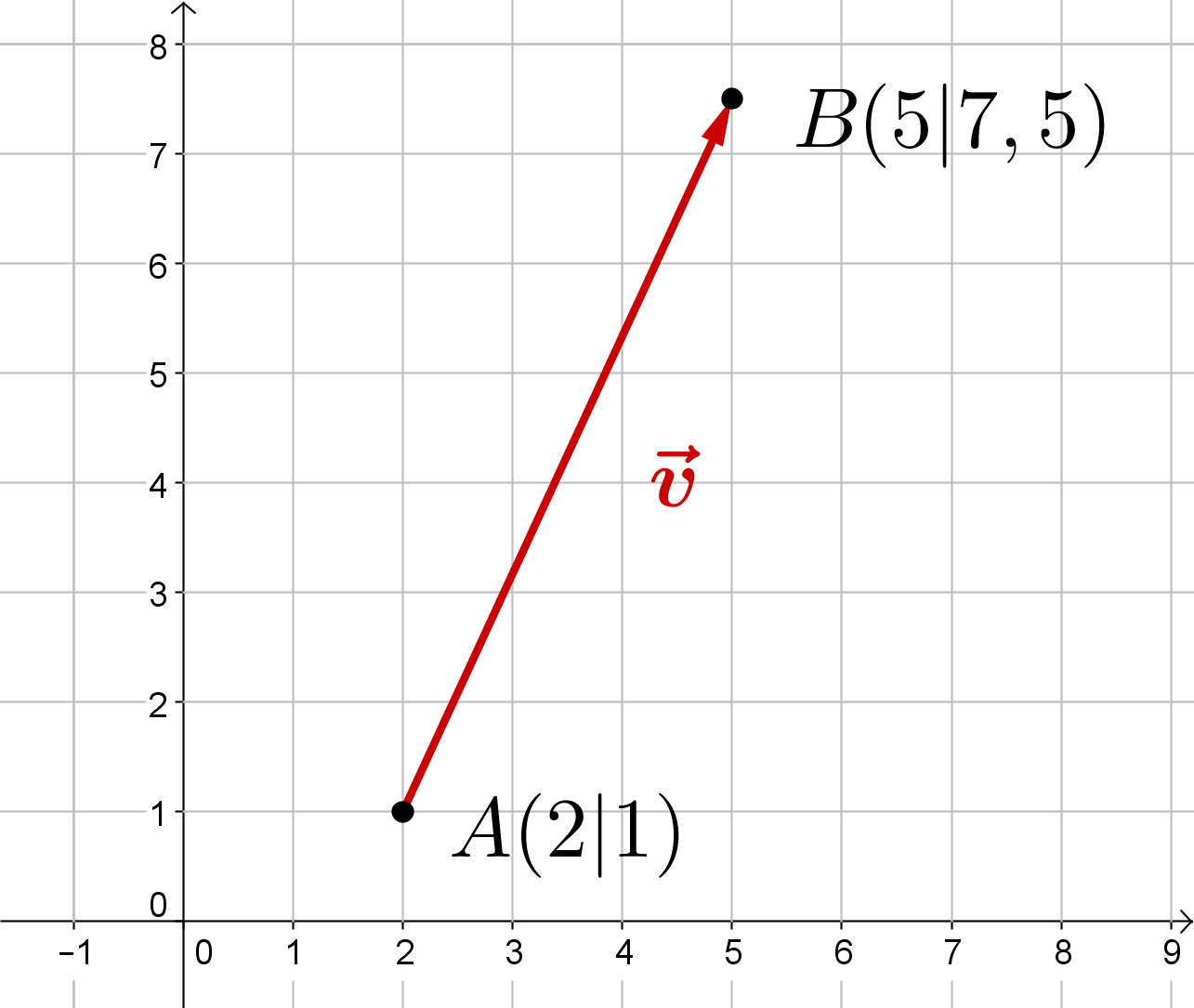
Bestimme die Koordinaten des Vektors, der im Bild zu sehen ist.
- 4
Bestimme die Koordinaten des Vektors mit Fußpunkt und Spitze .
,
,
,
,
- 5
Bestimme die Koordinaten des angegebenen Vektors
Der Vektor verläuft von Punkt zum Punkt .
Vektor hat Fuß und Spitze .
hat Fuß und Spitze .
- 6
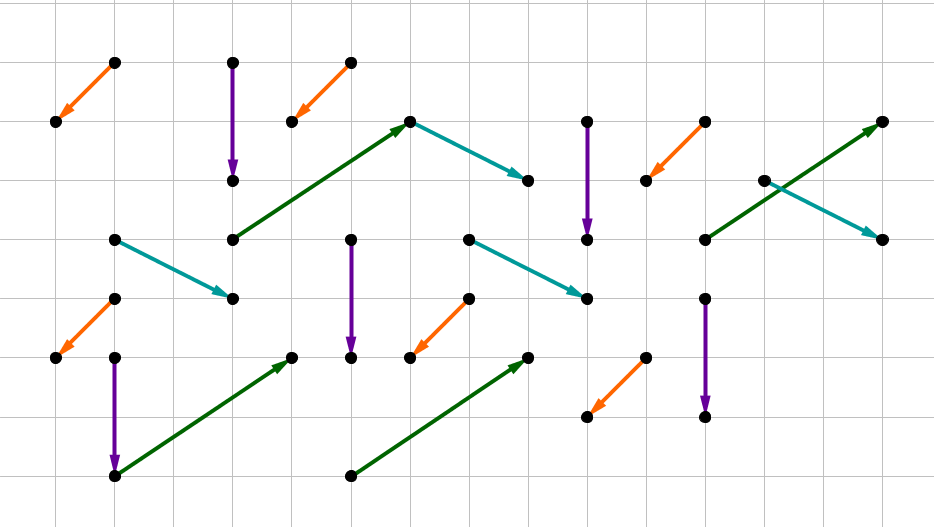
Gib alle im unteren Bild abgebildeten Vektoren an.

- 7
Bestimme jeweils die Koordinaten des Vektors und veranschauliche in den Teilaufgaben b) bis d) durch eine Zeichnung!
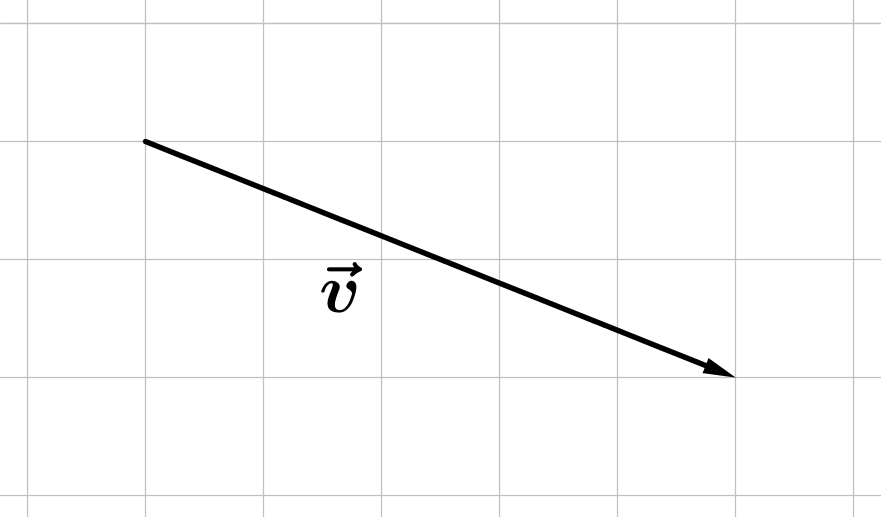
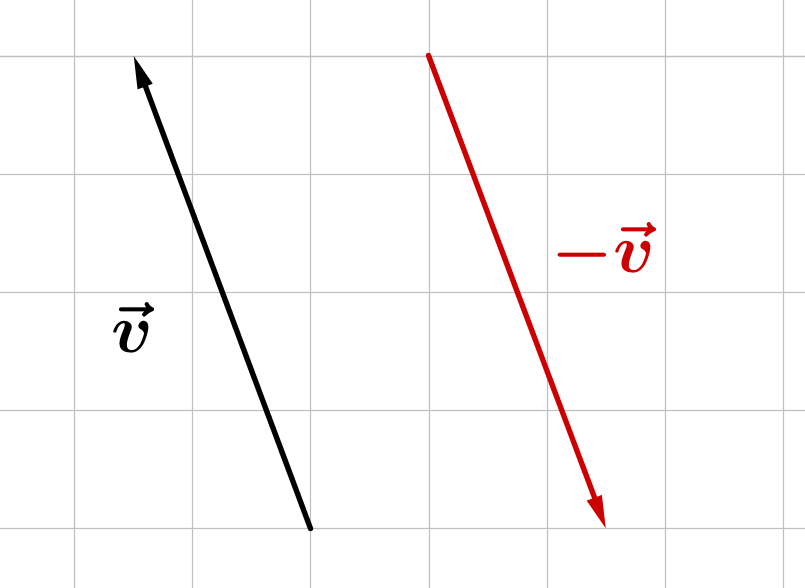
Gegenvektor von
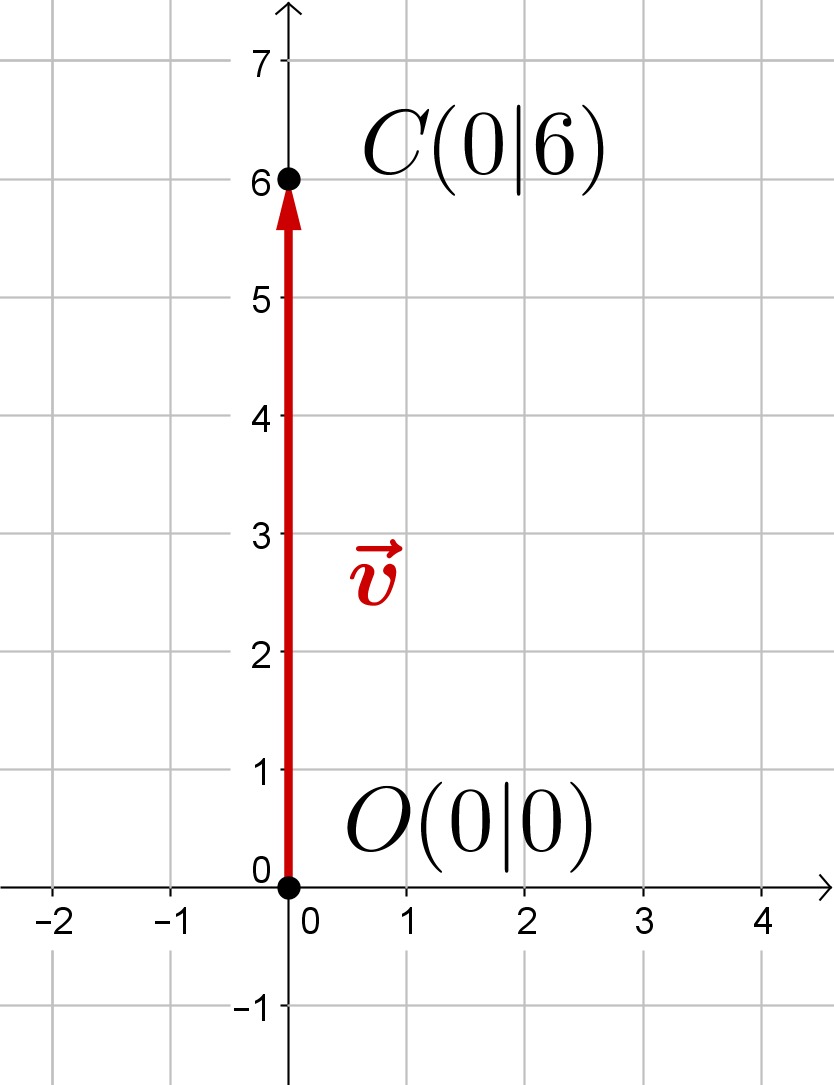
Ortsvektor von
- 8
Berechne zu den gegebenen Koordinaten jeweils den Verbindungsvektor .
Hinweis: Gib den Vektor als in das Feld ein.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?